正規分布を切断した場合の偏差値
2018/01/31
カテゴリ：数理統計
概要
身長の統計データを例に、母集団の違いが偏差値の算出に与える影響を実際に計算しました。
使用するデータ
文部科学省が実施する学校保健統計調査の2016年度の調査結果から、17歳の男性（高校3年生）の身長データを使用しました。
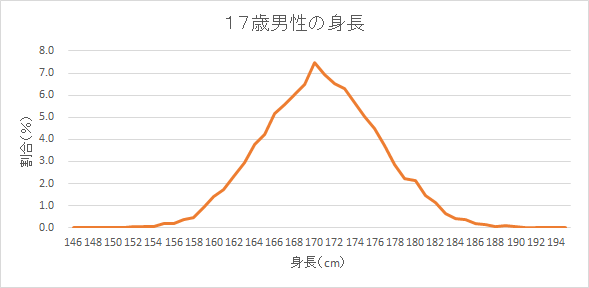
17歳男性の身長の分布
17歳の男性の平均身長は170.6cm、標準偏差は5.80cmです。
階級幅が1cmの割合データもあります。これをグラフに表すと次のようになります。
を、重ねて表示すると次のようになります。
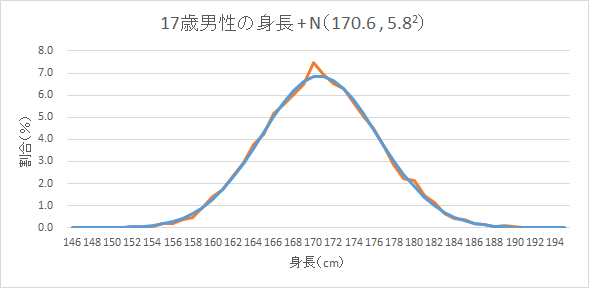
身長のデータは正規分布にとてもよく似た形状であることが分かります。
以下では、17歳男性の身長の分布が正確にに従うと仮定して計算します。
身長を偏差値に変換する
このとき、データの標準化得点を標準正規分布表と見比べることで、身長の相対的な位置がわかります。あるデータXについて、その標準化得点zは母平均
と母標準偏差
を用いて次のように計算します。
【参考】統計学の時間：14-3. 標準化したデータの使い方
また、標準化得点Zを10倍して50を加えると、偏差値Tとなります。
偏差値と聞くと受験や試験が連想されますが、 偏差値それ自体は集団内での相対的な位置を示す指標のひとつでしかありません。 標準化得点は0に近いほど平均に近く、偏差値は50に近いほど平均に近いことを表します。
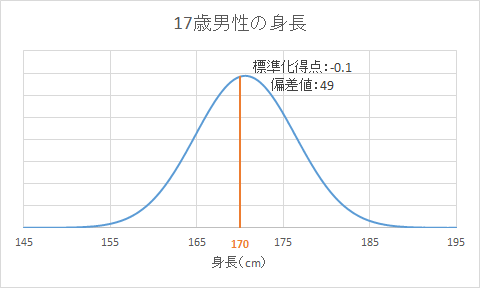
仮に、17歳で170cmの男性a氏がいたとします。
A氏の標準化得点
は-0.1で、偏差値
は49と計算できます。
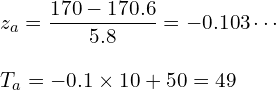
正規分布に近い分布である場合、正規分布表から標準化得点zを順位に換算できます。 およそ100人中54位です。
【参考】統計学の時間：14-5. 標準正規分布表の使い方1
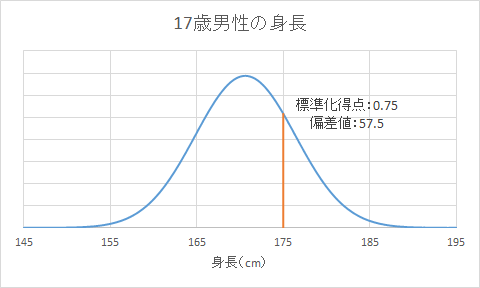
17歳で175cmのb氏についても考えます。
標準化得点
は0.76で、偏差値
は57.6です。
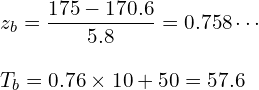
同様に順位に換算すると、およそ100人中23位です。
異なる母集団における偏差値を計算する
ここで17歳の男性を平均値を境界として、身長170.6cm以下の集団と身長170.6cmより大きい集団で二分します。 このとき、平均よりも背の高い集団において、身長175cmのb氏の偏差値はいくつになるでしょうか。
170.6cmより大きい17歳男性の集団を集団Aと呼びます。集団Aの分布をグラフに表すと次のようになります。 このような、正規分布の一部を切り取った分布を切断正規分布と呼びます。
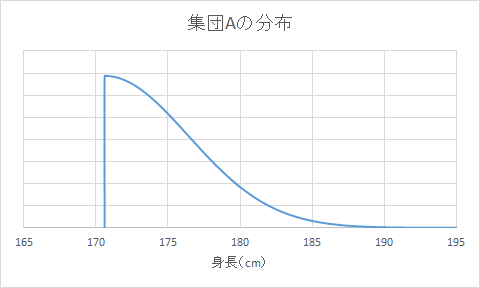
集団Aの平均は175.2cmで、標準偏差は3.5cmです。
片側を切断した切断正規分布の平均や標準偏差の計算方法については、別記事で解説します。
さて、母集団を集団Aとして考えたとき、身長175cmのb氏の偏差値を計算しましょう。 標準化得点は-0.07で、偏差値は49です。
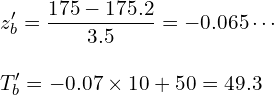
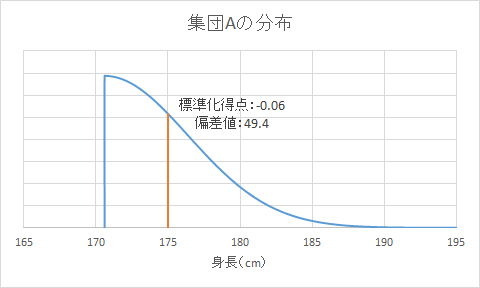
17歳男性全体においてb氏の偏差値は57でしたが、「平均より身長の高い17歳男性」に母集団を限定するとb氏の偏差値は49になりました。
このように、考慮する母集団が異なれば、同じデータでも偏差値は異なります。 これは、偏差値が母集団内での相対的な位置についての指標であるためです。
