2018年6月統計検定2級の問題の解説（その3）

2018/06/25

カテゴリ：統計検定

タグ：2018年6月, ブログ

※統計検定2級解説記事一覧はこちら※

下記のリンクからそれぞれの問題の解説に飛ぶことができます。

問12：母平均の差の検定に関する問題
問13：第一種の過誤、第二種の過誤に関する問題
問14：回帰分析に関する問題
問15：独立性の検定に関する問題
問16：等分散性の検定に関する問題

問12 [24]

2標本のt検定のための式を覚えておかなければ解けない問題でした。まず、セ・リーグ、およびパ・リーグの年間入場者数の不偏分散を求めます。

$\displaystyle s_{c}^2=\frac{13549}{6-1}=2709.8$

$\displaystyle s_{p}^2=\frac{7763}{6-1}=1552.6$

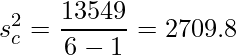
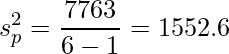
2標本t検定では次の式から検定統計量を求めます。

$\displaystyle t=\frac{233.7-185.3}{\sqrt{s^2 \left( \frac{1}{6}+\frac{1}{6} \right)}}=1.82$

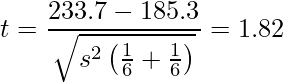
ただし、2標本をプールした分散を次の式から求めておきます。

$\displaystyle s^2=\frac{(6-1) \times 2709.8 + (6-1) \times 1552.6}{6+6-2}=\frac{2709.8 + 1552.6}{2}=2131.2$

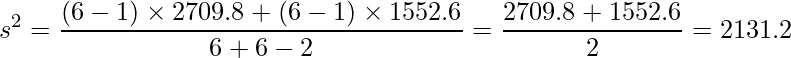
問12 [25]

この問題では、与えられた表から分散分析表を完成させる必要があります。何を計算するとどの部分の平方和が求められるのかをきちんと理解しておかなければ解けない、難問でした。

12球団まとめた全体の平均： $\frac{233.7+185.3}{2}=209.5$

リーグの効果による平方和： $(209.5-233.7)^2 \times 6+(209.5-185.3)^2 \times 6=7027.68$

残差による平方和： $13549+7763=21312$

これらの結果を分散分析表にまとめます。

因子	平方和	自由度	平均平方	F値
要因	7027.68	1	7027.68	3.30
残差	21312	10	2131.2
全体	28339.68	11

問13 [26]

第一種の過誤：帰無仮説が真であるのにもかかわらず、帰無仮説を偽として棄却してしまう誤りのこと。「第一種の過誤の確率＝有意水準」です。
第二種の過誤：帰無仮説が偽であるのにもかかわらずそれを真として棄却しない誤りのこと。

棄却域（帰無仮説を棄却する統計量の範囲）がX≤3のとき、

第一種の過誤の確率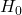： $H_0$ の下でX≤3となる確率=0.3
第二種の過誤の確率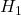： $H_1$ の下でX≥4となる確率=0.1
検出力＝1−第二種の過誤の確率：1−0.1=0.9

問13 [27]

この問題もやや難問でした。検出力が意味するところが具体的に分かっていないと解けない問題です。

棄却域（帰無仮説を棄却する統計量の範囲）がX≤2のとき、

第一種の過誤の確率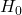： $H_0$ の下でX≤2となる確率=0.2
第二種の過誤の確率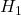： $H_1$ の下でX≥3となる確率=0.3
検出力=1−第二種の過誤の確率：1−0.3=0.7

棄却域（帰無仮説を棄却する統計量の範囲）がX=6のとき、

第一種の過誤の確率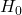： $H_0$ の下でX=6となる確率=0.3
第二種の過誤の確率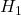： $H_1$ の下でX≠6となる確率=1.0
検出力=1−第二種の過誤の確率：1−1=0

問14 [28]

推定された重回帰モデルは次の式で表されます。

???⁡(犯罪発生率)=−7.09+0.094×失業率+2.418×???(賃金)−0.065×???(警察官数)

失業率＝2.8、???⁡(賃金)＝5.6、???⁡(警察官数)＝5.3を代入すると、???⁡(犯罪発生率)の予測値は

???⁡(犯罪発生率)=−7.09+0.094×2.8+2.418×5.6−0.065×5.3=6.4

となります。

問14 [29]

偏回帰係数の有意性の検定とは、定数項も含めた各偏回帰係数が0であるかについての検定結果です。この問題では帰無仮説は「偏回帰係数＝0.5」です。

次の式から算出される統計量t（t値）が自由度(n－k－1)のt分布に従うことを用いて検定を行います。nはサンプルサイズを、kは説明変数の数を表します。

$\displaystyle \frac{-0.06498-(-0.5)}{0.22718}=1.915$

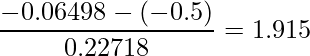
t分布表より、自由度47－3－1≒40の値を見ると、有意水準が10%の時には帰無仮説は棄却されます（1.684＜1.915）が、有意水準が5%の時には棄却されない（2.021＞1.915）ことが分かります。

問14 [30]

Ⅰ：〇
偏回帰係数が0かどうかに関する検定の結果のP値は「Pr(>|t|)」に記載されています。有意水準が1%のとき、有意となるものは「Intercept（定数項）」と「???⁡(賃金)」の2つです。

Ⅱ：×
???⁡(賃金)の偏回帰係数は「正」です。したがって、賃金が高いほど犯罪発生率は高い傾向があると予想されます。

Ⅲ：〇
自由度調整済み決定係数は「Adjusted R-squared」に記載されています。

問15 [31]

独立性の検定に関する基本知識を問う問題です。

「冬季」の日数：105＋15＝120
「風向きが北である」日数：105＋102＝207
すべての日数：365

したがって、「冬季」に「風向きが北である」期待度数は、

$\displaystyle \frac{120 \times 207}{365}=68.05$

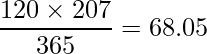
となります。

問15 [32]

独立性の検定を行うためのカイ二乗統計量は

「実測度数と期待度数の差の二乗」を「期待度数」で割ったものの総和

です。したがって次の式が正しい式です。

$\displaystyle \frac{(105-68.05)^2}{68.05}+\frac{(15-51.95)^2}{51.95}+\frac{(102-138.95)^2}{138.95}+\frac{(143-106.05)^2}{106.05}$

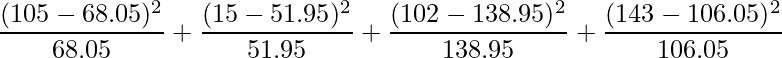
問15 [33]

m×n（縦がm行、横がn列）のクロス集計表の場合、自由度が(m－1)×(n－1)のカイ二乗分布を用いて検定を行います。この問題の場合(2－1)×(2－1)=1です。

したがって自由度「1」の「カイ二乗分布」を使用します。また、独立性の検定は片側検定で行います。統計数値表から上側確率が5%となる値を読み取ると「3.84」となっています。

カイ二乗統計量と比較すると69.04 > 3.84となることから、有意水準5%で帰無仮説（風向と季節は独立である＝風向と季節には関連がない）を棄却します。すなわち、風向と季節には関連があるといえます。

問16 [34]

等分散性の検定においてF統計量を算出するときには2つの分散のうち、大きな値の方を分子に、小さな値の方を分母にします。

$\displaystyle F=\frac{19.5^2}{14.5^2}=1.81$

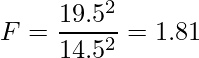
このF統計量を自由度(20, 40)のF分布を用いて検定します。F分布表より、自由度(20, 40)のF分布において上側2.5%点は「2.068」となっています。したがって1.81 < 2.068となり、有意水準5%では帰無仮説は棄却されません。

ブログ