※統計検定2級 解説記事一覧はこちら※

下記のリンクからそれぞれの問題の解説に飛ぶことができます。

• 問1：箱ひげ図に関する問題
• 問2：散布図に関する問題
• 問3：ローレンツ曲線とジニ係数に関する問題
• 問4：指数の計算に関する問題
• 問5：フィッシャーの3原則に関する問題
• 問6：標本抽出法に関する問題

問1 [1]

3つの箱ひげ図から適切なものを選んでいく問題です。見るべきポイントは縦軸（y軸）の値です。

Ⅰ：データが0を中心に、約‐2～2の間に散らばっています。このグラフは「標準化得点」を表しています。 標準化得点は、元のデータを標準化した値のことで、平均が0、分散が1となります。-2から2の間に全体の約95%のデータが含まれます。

Ⅱ：データが0を中心に、約‐25～30の間に散らばっています。このグラフは「偏差」を表しています。 偏差はデータの平均と各データとの差のことです。

Ⅲ：データが20～80の間に散らばっているのが読み取れます。このグラフは「総得点」を表しています。

問1 [2]

標準偏差に関する問題です。与えられた条件を丁寧に計算すればOKです。

• J2のチームの年間総得点の平均：54.45
• J2のチームの年間総得点の標準偏差：11.77

したがって、平均から標準偏差の2倍の範囲は「(54.45－2×11.77)から(54.45＋2×11.77)」までとなります。これを計算すると「30.91から77.99」までです。

この範囲から外れているデータは「名古屋　85」のみなので1個となります。

問2 [3]

散布図から相関関係を読み取る問題です。散布図と相関係数との関係をよく理解しておく必要があります。

Ⅰ：〇
正の相関とは「横軸の値（x）が増加すると縦軸の値（y）も増加するという関係」のことです。人口と常設映画館数との間にも同様の正の相関があることが分かります。

Ⅱ：〇
相関係数は外れ値の影響を受けやすいため、データを目で確かめることが必要です。このデータの場合東京都のせいで相関係数が高くなっていることが予想されます。

Ⅲ：×
人口と常設映画館数との間には正の相関があることが予想されます。

問2 [4]

[3]と同様に散布図の読み取り問題です。

Ⅰ：×
北海道と同程度の人口（約500万人）をもつ都府県の点の中で、北海道の点が最も上部（＝一般病院病床数が最も多い）にあります。

Ⅱ：〇
変動係数は標準偏差を平均で割ったものです。人口1人当たりの一般病院病床数の変動係数は、一般病院病床数の変動係数よりも小さくなることが予想されます。

Ⅲ：×
人口が多い9都道府県（＝人口500万人以上）のみを見てみてると、人口と一般病院病床数には正の相関があることが分かります。

問2 [5]

偏回帰係数が突然、単回帰モデルとともに出てきたので、難しく感じた方もいらっしゃるかもしれません。

Ⅰ：〇
偏相関係数とは第3の因子の影響を除いた相関係数のことです。e1とe2との相関係数は、人口の影響が除かれた変数同士の相関を意味しています。

Ⅱ：〇
常設映画館数が多いほど一般病院病床数も多いといった関係があるとは考えにくいため、両者の関係は擬相関だと考えられます。

Ⅲ：×
病院に映画館が併設されているかどうかはこの散布図からは分かりません。

問3 [6]

表中の第〇五分位階級までの累積割合が、ローレンツ曲線における20%ごとの「人口の累積相対度数」における「所得の累積相対度数」を表しています。

このローレンツ曲線は、

• 第1五分位階級＝人口の累積相対度数20%における所得の累積相対度数
• 第2五分位階級までの累積割合＝人口の累積相対度数40%における所得の累積相対度数
• 第3五分位階級までの累積割合＝人口の累積相対度数60%における所得の累積相対度数
• 第4五分位階級までの累積割合＝人口の累積相対度数80%における所得の累積相対度数
• 第5五分位階級までの累積割合＝人口の累積相対度数100%における所得の累積相対度数

を表します。

ドイツの所得の累積相対度数を計算すると「第1五分位階級（8.4%）」、「第2五分位階級（21.5%）」、「第3五分位階級（38.7%）」、「第4五分位階級（61.4%）」、「第5五分位階級（100%）」となり、図中のローレンツ曲線に当てはまります。

問3 [7]

ジニ係数は、完全平等線とローレンツ曲線との間の面積を2倍した値です。この問題では、ローレンツ曲線の細かいズレは気にせず、キリの良い点をすべて通っていると考えて計算します。

人口の累積相対度数において、20%ごとに面積を5つに分割して計算します。

• 0～20%の範囲の面積：0.1×0.2×0.5＝0.01
• 20～40%の範囲の面積：0.1×0.2×0.5＋ 0.2×0.2×0.5 ＝0.03
• 40～60%の範囲の面積：0.2×0.2×0.5＋ 0.2×0.2×0.5 ＝0.04
• 60～80%の範囲の面積：0.2×0.2×0.5＋ 0.2×0.2×0.5 ＝0.04
• 80～100%の範囲の面積：0.2×0.1×0.5＋ 0.1×0.2×0.5 ＝0.02

したがって、ジニ係数は2×(0.01＋0.03＋0.04＋0.04＋0.02)＝0.28となります。

問3 [8]

Ⅰ：〇
すべての国のローレンツ曲線が下に凸となります。

Ⅱ：×
日本、アメリカ、ドイツの中で一番下に弧を描く（完全平等線から遠い）のはアメリカであることから、アメリカのジニ係数が最も大きくなります。

Ⅲ：〇
スウェーデンと中国を比較した場合、中国のほうがより下に弧を描きます。したがって、中国のほうが不平等であると言えます。

問4 [9]

2010年に対する2011年の変化率を求めます。

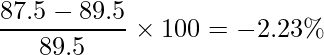
問4 [10]

式展開をミスらないようにゴリゴリ行う問題です。問題文に従って式を立てると次のようになります。

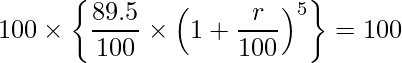
この式をrの計算式に直します。

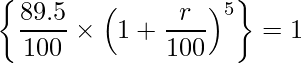
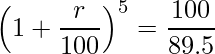
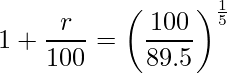
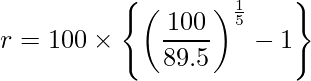
問5 [11]

フィッシャーの3原則は次の3つです。それぞれの法則が意味するところについてもしっかりと押さえておきましょう。（詳しくは統計学の時間 31-1章）

• 反復　もしくは　繰り返し（replication）
• 無作為化（randomization）
• 局所管理（local control）

問6 [12]

問題文の抽出法は「層化（層別）抽出法」です。これは、母集団をあらかじめいくつかの層（グループ）に分けておき、各層の中から必要な数の調査対象を無作為に抽出する方法のことです。

【例】男女比が7：3の高校で、10人の学生を対象に意識調査を行う場合、男子の中から7名を、女子の中から3名をそれぞれに無作為に抽出します。

【メリット】母集団内情報（年齢別、性別など）の比較を行える、母集団の推測の精度が増す、各層において分布が大きく異なる場合に使うことができる

【デメリット】母集団の構成情報を事前に知っておく必要がある