正規分布の分散を計算する の解説
2018/01/22
カテゴリ:数理統計
概要
ブログ記事「正規分布の分散を計算する」の解説記事です。
次の式で表される正規分布の分散(Vとします)が![]() となることについて、その計算の過程を補ったものです。
となることについて、その計算の過程を補ったものです。
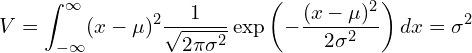
なお、数学的な記述についてはあまり込み入った解説はせず、高校卒業程度の知識で理解できる範囲に留めます。
ポイント
正規分布の分散を計算する上で、式変形のポイントが二つあります。
- 簡単な式に変形する
- 部分積分で計算する
置換積分により、![]() を
を![]() に変形します。
に変形します。
1.で変形した式に部分積分を適用し、![]() が
が![]() となることを計算します。
となることを計算します。
簡単な式に変形する
正規分布![]() の分散を求めるには、次の式の計算が必要です。
の分散を求めるには、次の式の計算が必要です。
(1) 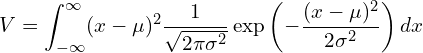
まず変数変換を行うのですが、正規分布の指数部分![]() が複雑な形をしています。
が複雑な形をしています。
このまま計算するのは煩雑です。そこで、次のような変換を行い![]() についての積分を考えます。
についての積分を考えます。
(2) ![]()
次の3つの点に注意しながら、元の積分を書き換えます。
- 積分区間
- 被積分関数
- dxとdyの関係
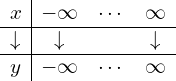
元々の積分区間は![]() がが
がが![]() から
から![]() までを考えていたのですが、
までを考えていたのですが、
![]() という変換によって、
という変換によって、![]() がどのように変化するか考えます。
がどのように変化するか考えます。
![]() も
も![]() から
から![]() まで値を取ることが分かります。つまり、積分区間は
まで値を取ることが分かります。つまり、積分区間は![]() です。
です。
被積分関数について、![]() を含む部分を全て
を含む部分を全て![]() に置き換えます。
に置き換えます。
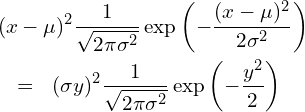
最後にdxです。(2)式を![]() についての式に変形します。
についての式に変形します。
これを、yについて微分します。
これを変形すると![]() と書き換えられます。
と書き換えられます。
以上のことから、(1)式の積分は次のように書き換えられます。
(3) 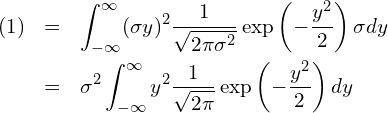
このような変数変換による積分の書き換えを置換積分と呼びます。 現在の学習指導要領では高校の数学IIIの範囲です。
部分積分で計算する
次に、部分積分による計算です。
部分積分は次の式で表される積分公式の一つです。![]() や
や![]() はそれぞれの関数を微分したものを表します。
はそれぞれの関数を微分したものを表します。
![Rendered by QuickLaTeX.com \displaystyle \int_a^b f(x)g(x)' dx = \left[ f(x)g(x) \right]_a^b - \int_a^b f(x)'g(x)dx](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-cd80efb1fb8ad895389d23b03a5c381b_l3.png)
まず、(3)式の被積分関数![]() を二つの関数の積
を二つの関数の積![]() で表せるか考えます。
で表せるか考えます。
やや唐突ですが、![]() について次の関係が成り立ちます。
について次の関係が成り立ちます。
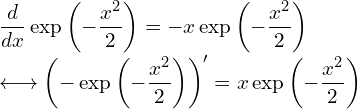
これを用いると、![]() の形をした関数を積分することができます。
の形をした関数を積分することができます。
![]() の積分
の積分![]() とおき、部分積分によって変形しましょう。
とおき、部分積分によって変形しましょう。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle \lefteqn{I_n = \int_{-\infty}^{\infty} x^n \exp \left(-\frac{x^2}{2} \right) dx} \\ &=& \int_{-\infty}^{\infty} x^{n-1} \times x \exp \left(-\frac{x^2}{2} \right) \\ &=& \int_{-\infty}^{\infty} x^{n-1} \left( - \exp \left(-\frac{x^2}{2} \right) \right)' dx\\ &=& \left[ x^{n-1} \left( - \exp \left( -\frac{x^2}{2} \right) \right) \right]_{-\infty }^{\infty } +(n-1) \int_{-\infty}^{\infty} x^{n-2} \exp(-\frac{x^2}{2}) dx \\ &=&\left[ -x^{n-1} \exp \left( -\frac{x^2}{2} \right) \right]_{-\infty }^{\infty } + (n-1) I_{n-2} \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-48a3808d27f46a782d0ba4d1b6b0ea23_l3.png)
最後の式の第1項が分かれば![]() と
と![]() は何らかの数列で表すことができそうです。
ここで、第1項は次のような極限となります。
は何らかの数列で表すことができそうです。
ここで、第1項は次のような極限となります。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle \lefteqn{ \left[ -x^{n-1} \exp \left(-\frac{x^2}{2} \right) \right]_{-\infty }^{\infty } } \\ &=&-\lim_{x \to \infty} x^{n-1} \exp \left( -\frac{x^2}{2} \right) + \lim_{ x \to -\infty} x^{n-1} \exp \left( -\frac{x^2}{2} \right) \\ &=& 0](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-6754a13ca668d9b23513df8ea80e5601_l3.png)
最後の変形には、![]() であることを用いました。
つまり、
であることを用いました。
つまり、
となります。
以上のことから、式(3)は次のように変形できます。
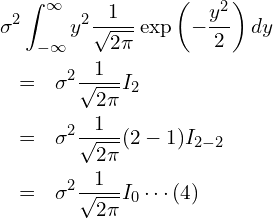
最後に![]() の値です。
ガウス積分でも計算できますが、確率分布についての知識があれば計算は不要です。
の値です。
ガウス積分でも計算できますが、確率分布についての知識があれば計算は不要です。![]() について、具体的にどのような式になっているのでしょうか。
について、具体的にどのような式になっているのでしょうか。
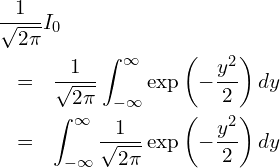
よく見ると、この式の被積分関数は標準正規分布の確率密度関数と全く同じであることが分かります。
ここで、確率分布の性質を思い出してみましょう。
統計学の時間でも解説していますが、確率密度関数はその定義から、全域で積分すると1となることが分かっています。
つまり![]() です。これを(4)に代入します。
です。これを(4)に代入します。
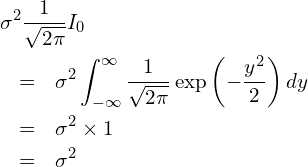
これで、正規分布の分散が![]() と求められました。
と求められました。








