正規分布の分散を計算する
2017/12/31
カテゴリ:数理統計
概要
正規分布![]() の分散は
の分散は![]() です。
です。
公式のように覚えてしまうのもよいのですが、実際に計算して![]() であることを確かめましょう。
であることを確かめましょう。
ただし本記事では、意図的に式展開や計算の根拠などの行間を省いている部分があります。 練習問題のように実際に計算して、行間を埋めてください。 行間は、来月の記事で解説します。
この記事の目安
- 統計検定でのおおよその目安
- 数学的な内容の目安
- 合成関数の微分
- 指数関数の微分
- 部分積分
- 積分の変数変換(置換積分)
統計検定2級の内容をある程度理解しており、統計検定準1級や統計検定1級に向けて勉強したい人
理系で高校を卒業した人、または次の内容を簡単に覚えている人
計算
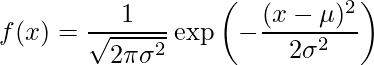
平均は![]() であるため、分散
であるため、分散![]() は次の式を計算すればよいことがわかります。
は次の式を計算すればよいことがわかります。
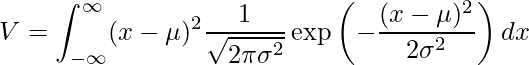
一見、とても難しそうです。 しかしこの計算は、変形によって簡単に計算することができます。
最初に、変数変換を行います。
![]() とおきましょう。
とおきましょう。
このとき、![]() となることから次のように変形できます。
となることから次のように変形できます。
![]() の積分区間についても忘れないようにしましょう。
の積分区間についても忘れないようにしましょう。
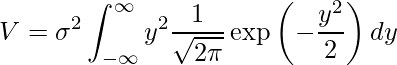
直接計算するにはまだ少し難しいので、部分積分を行います。
どのように変形すればよいかを検討するため、
![]() を微分しましょう。
を微分しましょう。
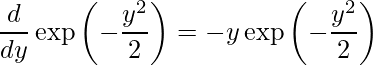
これを利用すると、与式は次のように書き換えることができます。
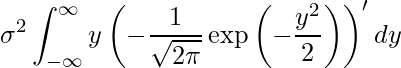
部分積分を行うと、次のように計算できます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle \lefteqn{\sigma^2 \int_{-\infty }^{\infty} y \left(- \frac{1}{\sqrt{2\pi}} \exp \left(-\frac{y^2} {2} \right) \right)' dy} \\ &=& \sigma^2 \left[ -y \frac{1}{\sqrt{2\pi}} \exp \left(-\frac{y^2} {2} \right) \right]_{-\infty }^{\infty} + \sigma^2 \int_{-\infty }^{\infty} \frac{1}{\sqrt{2\pi}} \exp \left(-\frac{y^2} {2} \right) dy \\ &=& \sigma^2 \times 0 + \sigma^2 \times 1 \\ &=& \sigma^2 \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-e2a5c614ff976f3d8de5f7c99492bc1d_l3.png)
以上のことから、正規分布の分散が![]() と求められました。
と求められました。








