※コラム「統計備忘録」の記事一覧はこちら※

統計ソフトを使ってロジスティック回帰分析を行うと、ほとんどのソフトでは以下の数値が出力されます。

(1)分析に用いた変数の基本統計量
(2)回帰式の偏回帰係数と信頼区間
(3)偏回帰係数のカイ二乗検定結果
(4)オッズ比と信頼区間
(5)回帰モデルの対数尤度

「ダミー変数」の記事中のデータをエクセル統計（正確にはエクセル統計2006からですが）で分析すると出力は次のとおりです。

エクセル統計2006のロジスティック回帰分析出力*

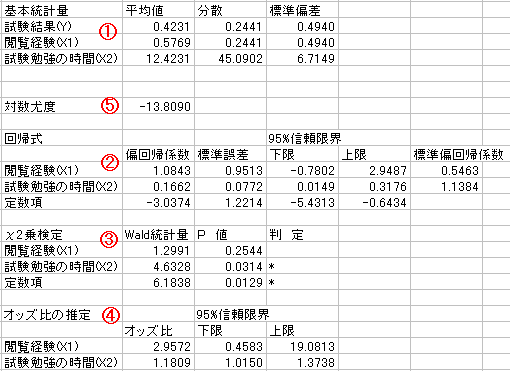
(1)の平均や分散については、ブログ「ダミー変数」の記事を参考にしてください。(2)の偏回帰係数は「ロジステッィク変換の逆変換」書いたようにロジットを求めるためのものですから、重回帰分析とは解釈の仕方が異なります。偏回帰係数がちょうどゼロだとロジットに影響を与えない、最終的に確率を上げも下げもしません。係数がプラスの場合は確率を上げ、マイナスだと確率を下げる方向に働きます。この例では、統計WEBの閲覧経験も試験勉強の時間も係数がプラスなので、試験を合格させる効果があるということになります。

(3)は偏回帰係数の検定ですが、これは「偏回帰係数 = 0」という帰無仮説を検定しています。各偏回帰係数のWald統計量（検定のための統計量。カイ二乗分布します）についてのP値が有意水準を下回れば、有意な偏回帰係数と言えます。この例では、試験勉強の時間（X2）がP=0.0314と5%未満で有意です。残念ながら統計WEBの閲覧経験はP=0.2544で5%を超えて有意とは言えません。

(4)のオッズ比については「統計WEBの効果」の記事に書いた通りです。ここには95%信頼限界の出力がありますが、下限と上限の間に1を含むかどうかのチェックを忘れないでください。なお、（2）のところにも95%信頼限界の出力がありますが、これは偏回帰係数の信頼区間です。こちらは、信頼区間にゼロを含む（下限と上限の符号が異なる）かどうかをチェックします。2つの信頼区間は対応しています。

(5)の対数尤度ですが、これは回帰モデルの式の尤（もっと）もらしさの指標になります。幾つかの説明変数の候補がある場合、説明変数の組み合わせを変えて幾つかの分析をすることになると思います。その結果得られた対数尤度同士を比較して、値の高いほうがより尤もらしいということになります。重回帰分析の決定係数のように1に近ければ良いというような見方はしませんので、説明変数の候補が1組しかないのなら対数尤度は見ません。

なお、ロジスティック回帰分析で変数を絞り込む場合、p＜0.05の変数だけにすると重要な変数を落としてしまう危険があるため、P＜0.15かP＜0.2まで条件を緩めて分析することが多いようです。

さて、(4)のオッズ比に話を戻します。試験勉強の時間（X2）はカテゴリー変数ではないので、色々な値をとります。しかし、（4）のオッズ比は1時間勉強を増やすと、どれだけ合格の確率が上がるかを示しているだけです。10時間勉強した場合の効果を知りたければ、このオッズ比を10乗してください。10時間の効果は勉強を全くしなかった人の5.27倍ということになります。

エクセル統計の出力にはシミュレーションのセクションがあります。ここには、オッズ比やロジット、そして、ロジットを逆変換して確率を求める計算式が埋め込んであります。各説明変数の値を自由に入力して、どのような値が得られるか、ソフトをお持ちの方は試してみてください。

シミュレーション・セクション（閲覧経験あり、10時間勉強の場合）

*エクセル統計では、「偏回帰係数がゼロ」を帰無仮説とした尤度比検定の結果が出力されます。