2016年11月統計検定2級の問題の解説(その3)
2017/06/20
カテゴリ:統計検定
※統計検定2級 解説記事一覧はこちら※
2級の範囲を超えていますが、この問題は多変量正規分布の問題として解くこともできます。そのために必要な多変量正規分布の性質を紹介します。ある確率変数ベクトル![]() が平均
が平均![]() 、共分散行列
、共分散行列![]() の多変量正規分布に従うとき、線型変換
の多変量正規分布に従うとき、線型変換![]() を行った場合
を行った場合![]() は次のような多変量正規分布に従います。
は次のような多変量正規分布に従います。
まず、XとYを合わせて確率変数ベクトル![]() 、UとVを合わせて確率変数ベクトル
、UとVを合わせて確率変数ベクトル![]() とおきます。wは次の多変量正規分布に従います。
とおきます。wは次の多変量正規分布に従います。
2016年11月に実施された統計検定2級の問題の解説をしています。
この記事では、次の6問の解説をしています。下のリストからクリック、またはタップした問題の解説部分へジャンプします。
問12(回答番号23,24)
■回答番号23
![]() は、
は、![]() の標本平均と考えることができます。
の標本平均と考えることができます。![]() はベルヌーイ分布に従うので
はベルヌーイ分布に従うので![]() です。これと標本平均の分散の関係を用いると、
です。これと標本平均の分散の関係を用いると、![]() は次のようになります。
は次のようになります。
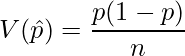
これは明らかに![]() の時に最大値を取り、その値は
の時に最大値を取り、その値は![]() です。
です。
■回答番号24
対立仮説が![]() となっていることから、これは両側検定です。有意水準が5%であるため、標準正規分布表より両側で5%、つまり片側が2.5%となるZの値を探すとZ=1.96です。つまり、この検定の棄却域は
となっていることから、これは両側検定です。有意水準が5%であるため、標準正規分布表より両側で5%、つまり片側が2.5%となるZの値を探すとZ=1.96です。つまり、この検定の棄却域は![]() です。以上の事から、
です。以上の事から、![]() のときに帰無仮説を棄却すればよい、という検定であることが分かります。
のときに帰無仮説を棄却すればよい、という検定であることが分かります。
問13(回答番号25,26,27)
■回答番号25
独立性の検定における期待度数の計算と同様です。総度数は192、夏季の行和は96、「100人以上120人未満」の列和は67であることから、次のように計算できます。
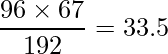
■回答番号26
二つの階級を併合したため、併合後のクロス集計表は「2行×5列」になります。この表からカイ二乗検定を行う場合、その自由度は![]() となります。
となります。
■回答番号27
カイ二乗分布表より、自由度4のカイ二乗分布の上側5%点は9.49と読み取れます。検定統計量はこれより大きいため、帰無仮説を棄却し「二つの分布は同等であるとは考えられない」と結論付けられます。
問14(回答番号28)
■回答番号28
対応のあるt検定の検定統計量を、表より数値を読み取って計算します。必要なのは「増分の平均」、「標準偏差」、「サンプルサイズ」です。
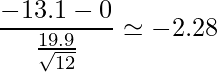
これは自由度11のt分布に従います。
問15(回答番号29,30,31)
■回答番号29
独立に同一の分布に従う標本平均の平均と分散の性質を用いると、![]() の分散は次のように求めることが出来ます。
の分散は次のように求めることが出来ます。
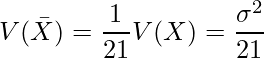
■回答番号30
有意水準5%の両側検定であることから、標準正規分布表より片側2.5%の点を読み取ります。この値はZ=1.96です。分散が未知の場合には、文中の統計量Tは1標本t検定の検定統計量そのものですから、自由度20のt分布表の両側5%点を読み取ります。この値は2.086です。もし、何らかの仮定のもと正規分布として考えられる場合には、Tは標準正規分布に従います。このとき、棄却域は(ア)と同じものとなります。
■回答番号31
Z=0.63における右片側の面積は0.2643です。これは片側のみを考慮した値であるため、両側P値はこの値を2倍します。よって、両側P値は0.5286となります。有意水準よりも大きいため、帰無仮説を棄却することはできません。
問16(回答番号32,33,34)
■回答番号32
各選択肢の正誤は次の通りです。
 誤:回帰モデルの自由度は195です。決定係数から算出するものではありません。
誤:回帰モデルの自由度は195です。決定係数から算出するものではありません。 誤:決定係数は確率的な解釈をする指標ではありません。
誤:決定係数は確率的な解釈をする指標ではありません。 誤:説明変数と目的変数を入れ替えた結果は逆数になるとは限りません。
誤:説明変数と目的変数を入れ替えた結果は逆数になるとは限りません。 正:残差の平均値は、常に0になります。
正:残差の平均値は、常に0になります。 誤:単回帰分析の分散分析表は、帰無仮説「傾き=0である」の検定の結果を表します。
誤:単回帰分析の分散分析表は、帰無仮説「傾き=0である」の検定の結果を表します。
■回答番号33
残差は「観測値―予測値」で定義されます。これについては、統計学の時間27章の記事も参照してください。
各選択肢の正誤は次の通りです。
 正:正しい残差プロットです。
正:正しい残差プロットです。 誤:元のグラフより、Creが最大の点(右端)と2番目に大きい点を見ると、「Cre最大の点の残差」>「2番目の点の残差」となるはずが、この残差プロットでは同じくらいの値となっているため不適です。
誤:元のグラフより、Creが最大の点(右端)と2番目に大きい点を見ると、「Cre最大の点の残差」>「2番目の点の残差」となるはずが、この残差プロットでは同じくらいの値となっているため不適です。 誤:符号が逆であるため不適です。
誤:符号が逆であるため不適です。 誤:Cre=1.4上の2点の残差がどちらも正の値になっていますが、元のグラフと矛盾しているため不適です。
誤:Cre=1.4上の2点の残差がどちらも正の値になっていますが、元のグラフと矛盾しているため不適です。
■回答番号34
回帰分析では、偏回帰係数の推定量![]() について次の統計量Tは自由度n-(偏回帰係数の数)-1のt分布に従います。偏回帰係数の標準誤差を
について次の統計量Tは自由度n-(偏回帰係数の数)-1のt分布に従います。偏回帰係数の標準誤差を![]() と表します。
と表します。
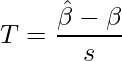
出力結果から推定値と標準誤差を読み取ると、統計量Tは次のようになります。
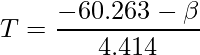
これは自由度195のt分布に従います。自由度nのt分布の左側a%点を![]() と表すと、次のように90%信頼区間を構成することができます。
と表すと、次のように90%信頼区間を構成することができます。
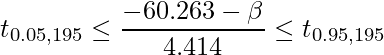
自由度195のt分布については表にはないので、120か240を代用します。今回は240を用います。他にも、nが十分大きいと見なしてt分布ではなく正規分布を用いることも出来ます。いずれの方法で計算しても結論は大きく変化しません。
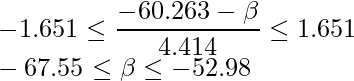
なお、分布の対称性より![]() が成立することを使用しています。
が成立することを使用しています。
2016年11月問題の解説
- その3:問12~問16(本記事)







