- Step1. 基礎編
- 27. 回帰分析
27-4. 予測値と残差
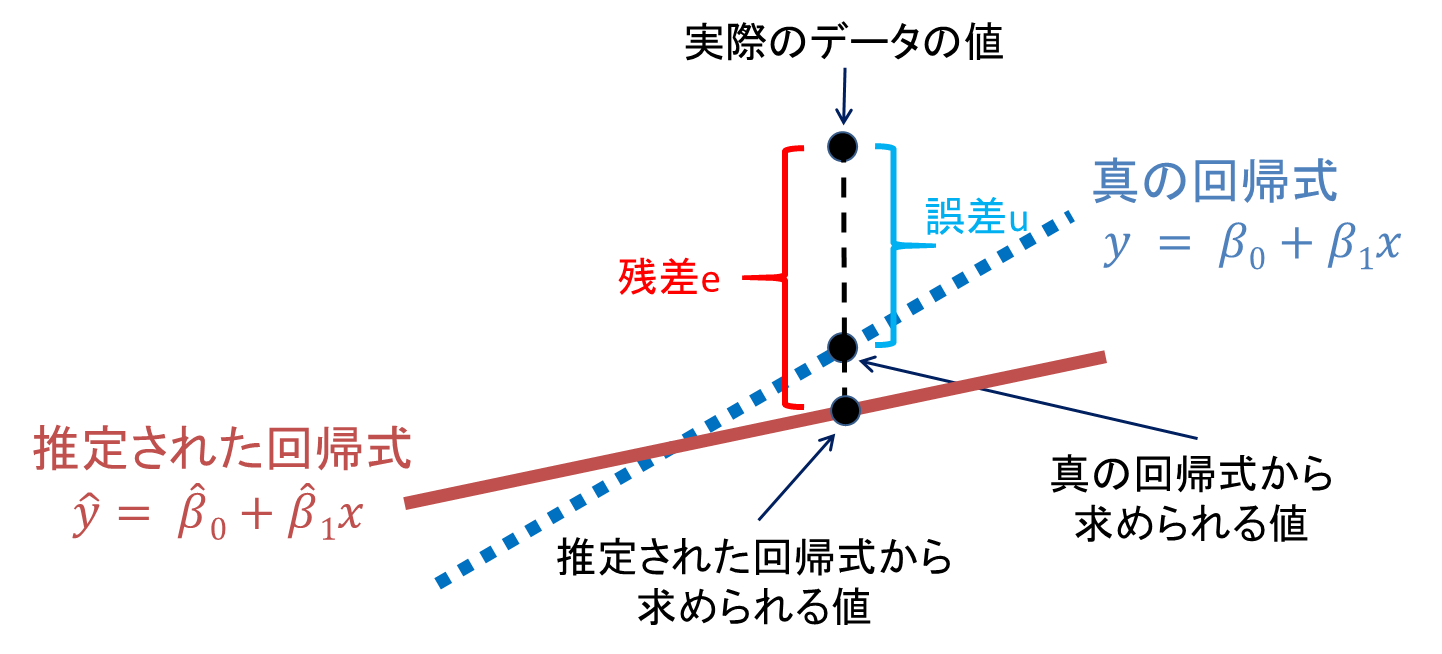
データから回帰式を推定すると、データの「予測値」が算出できます。これは、ある値xから予測される![]() の値のことです。27‐1章で示した、
の値のことです。27‐1章で示した、![]() を人口10万人あたりの薬局の数、
を人口10万人あたりの薬局の数、![]() を人口密度とした場合のデータから求められた回帰式を使って予測値を求めてみます。回帰式は
を人口密度とした場合のデータから求められた回帰式を使って予測値を求めてみます。回帰式は
と推定されました。この式を使うと、例えば人口密度が100人/![]() のときに予測される人口10万人あたりの薬局の数は次のように求められます。
のときに予測される人口10万人あたりの薬局の数は次のように求められます。
実際の人口密度のデータ![]() を回帰式に代入して得られた
を回帰式に代入して得られた![]() の値と、実際の薬局の数のデータ
の値と、実際の薬局の数のデータ![]() との差は「回帰残差」、あるいは簡単に「残差」とよばれます。
との差は「回帰残差」、あるいは簡単に「残差」とよばれます。![]() 番目のデータの残差を「
番目のデータの残差を「![]() 」を用いて表すと、
」を用いて表すと、
となります。
■残差と誤差
27-1章で出てきた「誤差![]() 」と、この章で出てきた「残差
」と、この章で出てきた「残差![]() 」は似ているように見えますが、異なる意味を持ちます。「誤差
」は似ているように見えますが、異なる意味を持ちます。「誤差![]() 」は求めようとする真の回帰式から算出される値と実際のデータとの差を表します。真の回帰式はあくまでも理論的なものであるため、誤差を計算で求めることはできません。一方の「残差
」は求めようとする真の回帰式から算出される値と実際のデータとの差を表します。真の回帰式はあくまでも理論的なものであるため、誤差を計算で求めることはできません。一方の「残差![]() 」は実際のデータを用いて推定された回帰式から算出される値と実際のデータとの差を表します。誤差とは異なり残差は計算で求められます。
」は実際のデータを用いて推定された回帰式から算出される値と実際のデータとの差を表します。誤差とは異なり残差は計算で求められます。
■残差の性質
残差にはいくつかの性質があります。
- 残差の総和は0である
- 説明変数
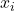 と残差
と残差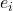 の積和は0である(この式は、説明変数
の積和は0である(この式は、説明変数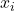 と残差
と残差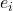 との間には相関がない(=無相関である)ということを表します)
との間には相関がない(=無相関である)ということを表します)
■残差の評価
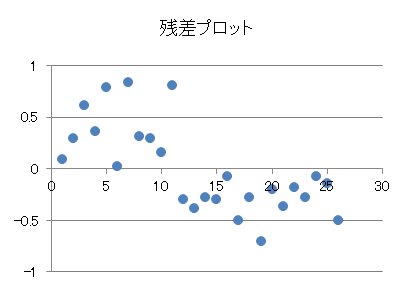
回帰式を評価する方法には、決定係数(27-4章で説明します)を算出する方法の他に、残差のばらつきを見る「残差分析」という方法があります。回帰式がデータに対して妥当であれば、残差は適当にばらつきます(分散均一性といいます)。これをチェックするために、各データの残差を左から順番に並べた「残差プロット」というグラフを作成します。横軸はデータの番号を、縦軸は残差の値を表します。
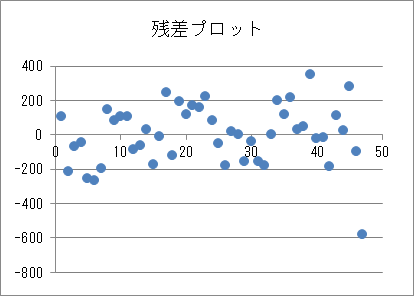
残差プロットでは、縦軸の「0」に対して、残差がどのようにばらついているかを確認します。残差が縦軸「0」に対して均一に分散している場合、大きな問題はありません。残差プロットの中で他とは異なり大きく外れている値が少数ある場合、該当する値は外れ値である可能性があります。
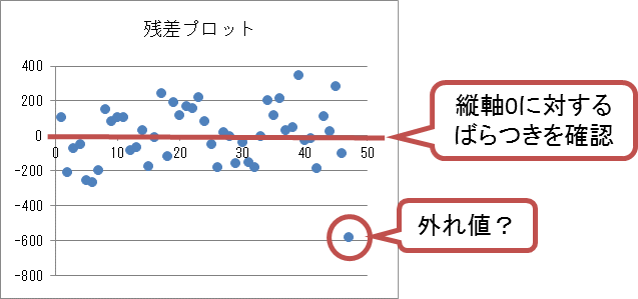
また、次のグラフに示すように、残差が徐々に大きくあるいは小さくなっていたり、何かしらの傾向が見られる場合は要注意です。この場合、推定された回帰式が妥当ではない可能性があります。
27. 回帰分析
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 12. 累積分布関数と確率変数の期待値・分散
12-5. 確率変数の分散
- 26. 相関分析
26-3. 相関係数
- 統計学で使う数学
シグマ(Σ)
- ブログ
回帰係数と相関係数
- ブログ
Excelで重回帰分析(1)
- ブログ
重回帰分析ができない