- 27. 回帰分析
練習問題(27. 回帰分析)
1
野球選手の「球速 [km/h]」を目的変数とし、「遠投 [m]」、「懸垂 [回]」、「握力 [kg]」を説明変数とした重回帰分析を行ったところ、次のような結果が得られた。この重回帰式において、「遠投」以外の変数が全て固定された状態で「遠投」が1m増加した時の「球速」の予測値の増加量はいくらか。
| 変数 | 偏回帰係数 | 標準誤差 | P値 |
|---|---|---|---|
| 遠投 | 0.7112 | 0.2556 | 0.0133 |
| 懸垂 | 0.3764 | 0.1909 | 0.0662 |
| 握力 | 0.0648 | 0.1960 | 0.7453 |
| 定数項 | 48.0687 | 19.0678 | 0.0227 |

答えを見る
- 答え
 閉じる
閉じる -
球速を
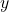 、遠投を
、遠投を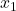 、懸垂を
、懸垂を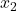 、握力を
、握力を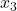 とすると、この分析で求めた重回帰式は次のようになることが分かります。
とすると、この分析で求めた重回帰式は次のようになることが分かります。
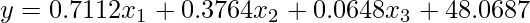
偏回帰係数は「それ以外の説明変数の値を固定し、その説明変数の値を1単位量増加させたときの
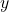 の増加量」であるので、「遠投」の偏回帰係数である「0.7112」が答えとなります。
の増加量」であるので、「遠投」の偏回帰係数である「0.7112」が答えとなります。
2
重回帰式の当てはまりのよさを知るには、どの指標を見ればよいか。
- 偏回帰係数のP値
- 自由度調整済み決定係数
- 重相関係数
- 偏回帰係数の値

答えを見る
- 答え
 閉じる
閉じる -
- ×:個々の偏回帰係数の有意性を見るための指標です。
- ◯:正しいです。
- ×:重相関係数は回帰式と予測値の相関係数であるため、回帰式の当てはまりを評価する指標です。ただし、決定係数と同様に変数が増えるとその値も増えるため、それを調整した値(自由度調整済み決定係数や自由度修正済み重相関係数)を見る方がより適しています。
- ×:偏回帰係数の大小を表すものであり、回帰式全体の当てはまりを評価する指標ではありません。
3
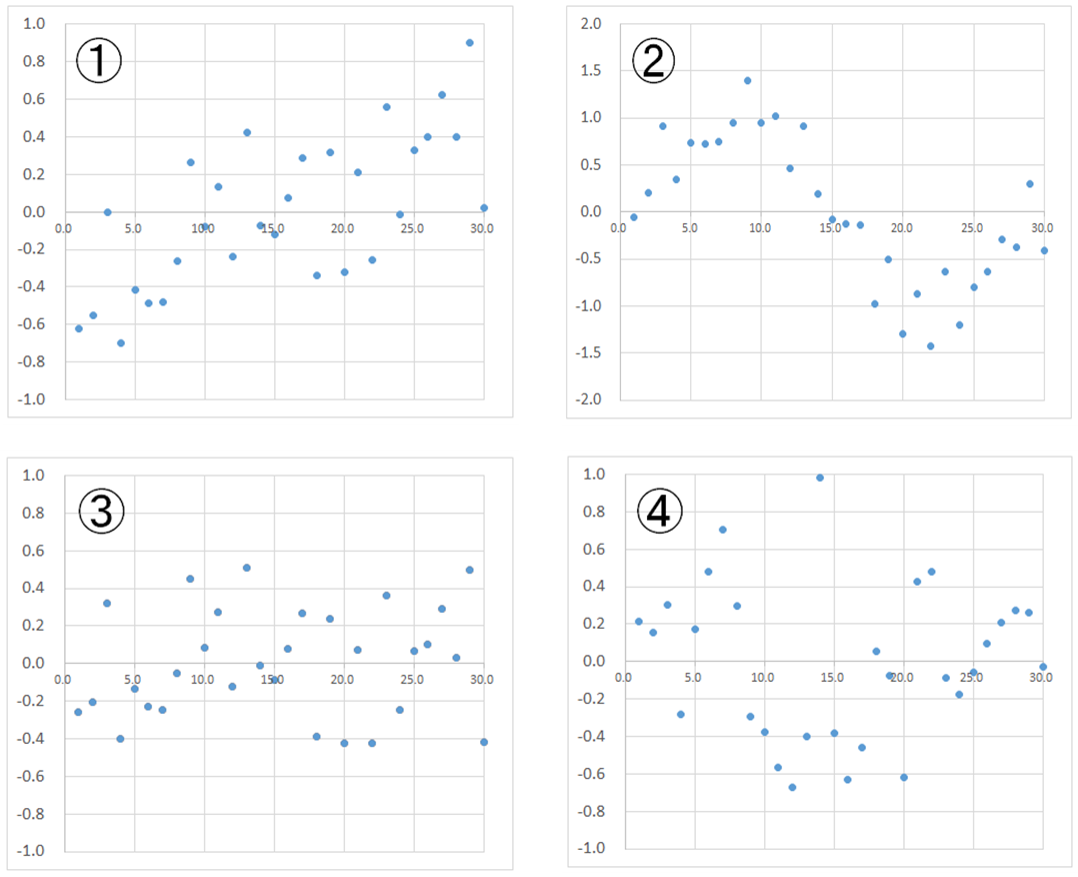
4つのデータに対して重回帰分析を行ったところ、次のような残差プロットが得られた。このうち、分析が適切に行われていると考えられるものを選べ。

答えを見る
- 答え
 閉じる
閉じる -
重回帰式における残差プロットでは、下記の2点に着目します。
- 段々上がっていく、下がっていくなどの傾向性がないか
- どの点でも散らばり具合は等しいか
- ×:残差が負から正になっている傾向がみられるので誤りです。
- ×:周期的に変化している傾向がみられるので誤りです。
- ◯:特に傾向もなく一様に散らばっているので正しいと考えられます。
- ×:分散が中ほどで大きくなっているため誤りです。
4
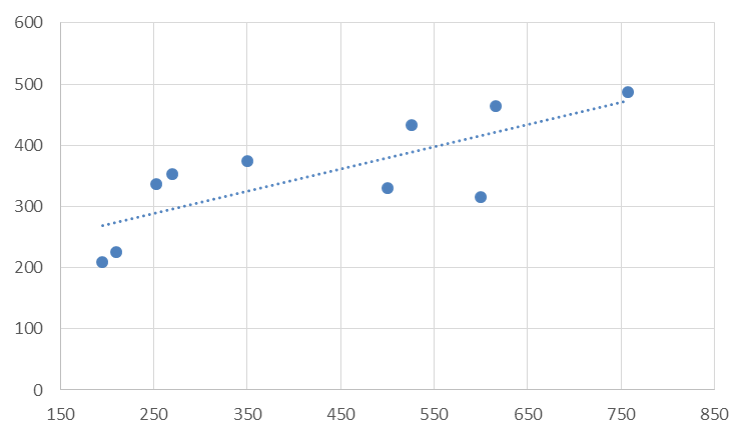
次のグラフは、あるデータから得られた散布図に単回帰直線(![]() )を加えたものである。この単回帰直線の回帰係数の組み合わせとして最も適切なものを選べ。
)を加えたものである。この単回帰直線の回帰係数の組み合わせとして最も適切なものを選べ。
- a=0.36, b=200
- a=0.52, b=200
- a=0.36, b=250
- a=0.52, b=250

答えを見る
- 答え
 閉じる
閉じる -
aは単回帰直線の傾きなので、グラフの任意の2点から傾きを求めます。例えば(250, 290)と(550, 400)を使うと、
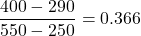 となります。
となります。
また、bは単回帰直線の切片です。このグラフの
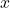 軸が「150」から始まっていることに注意すると切片は約200であることが分かります。したがって、正解は「1」です。
軸が「150」から始まっていることに注意すると切片は約200であることが分かります。したがって、正解は「1」です。
5
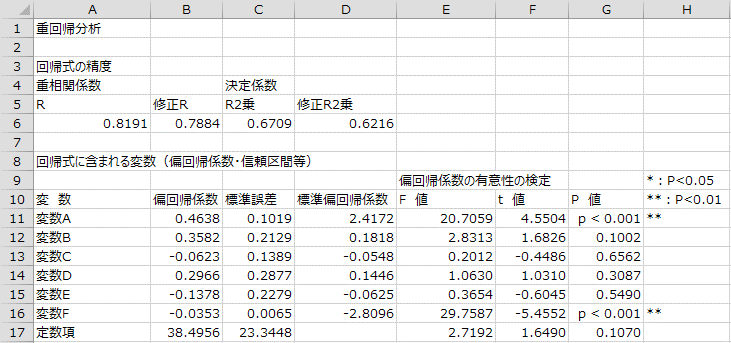
次の結果は、変数A~Fと目的変数からなるデータを用いて、エクセル統計で重回帰分析を行った結果である。この結果から、目的変数は変数A~Fによってどの程度説明できているか。
- 81.9%
- 78.8%
- 67.1%
- 62.2%

答えを見る
- 答え
 閉じる
閉じる -
回帰式の当てはまりのよさを調べるには「回帰式の精度」の部分を見ます。
重相関係数は、実際に観測された目的変数の値と重回帰式をあてはめて計算した推定値(理論値)との相関係数です。一方の決定係数は、目的変数の全変動のうち重回帰式で説明できる変動の割合です。したがって、説明変数が目的変数のどれくらいを説明できるかを見るには決定係数の値を使います。
ただし、説明変数の数が多い場合には、決定係数ではなく「自由度調整済み決定係数(自由度修正済み決定係数)」を使います。以上から正解は「4」になります。






