- Step1. 基礎編
- 27. 回帰分析
27-3. 重回帰分析
重回帰分析は複数の説明変数![]() (i=1, 2, 3, ・・・)を用いて目的変数
(i=1, 2, 3, ・・・)を用いて目的変数![]() を表す回帰式を算出することです。例えば、次のようなデータについて考えてみます。
を表す回帰式を算出することです。例えば、次のようなデータについて考えてみます。
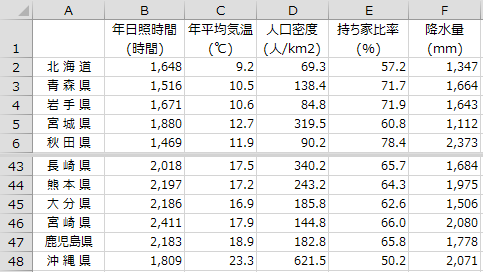
出典:総務省統計局 社会生活統計指標-都道府県の指標-2015
このデータでは年日照時間を目的変数![]() とし、残りの4変数を説明変数とします。年平均気温を
とし、残りの4変数を説明変数とします。年平均気温を![]() 、人口密度を
、人口密度を![]() 、持ち家比率を
、持ち家比率を![]() 、降水量を
、降水量を![]() とするとき、次のような重回帰式を求めることを考えます。
とするとき、次のような重回帰式を求めることを考えます。
重回帰分析の偏回帰係数も、単回帰分析と同様に最小二乗法で求めます。このデータを用いてエクセル統計で重回帰分析を行うと、偏回帰係数について次のような結果が得られます。

■偏回帰係数
偏回帰係数は上で示した式の![]() (i=0, 1, 2, 3, 4)の推定値です。定数項は切片のことで、
(i=0, 1, 2, 3, 4)の推定値です。定数項は切片のことで、![]() の値を示します。これらの値から、重回帰式は次のようになります。
の値を示します。これらの値から、重回帰式は次のようになります。
ある偏回帰係数は、それ以外の説明変数の値を固定した(変化させない)場合に、その説明変数が1増加するとyがどれだけ増加/減少するかを示しています。例えば、人口密度、持ち家比率、降水量を固定した場合、年平均気温が1℃上がると年日照時間が77.2時間増加すると考えられます。
■標準偏回帰係数
標準偏回帰係数は、説明変数および目的変数をそれぞれ標準化した値から算出される偏回帰係数のことです。標準偏回帰係数は重回帰式における各変数の重要性を表す指標であり、標準化偏回帰係数どうしの大小を比較できます。
例えば上に示したデータの場合、人口密度の標準偏回帰係数0.19と比較して年平均気温0.72の方が大きいことから、年平均気温の方が目的変数に与える影響が大きいことが分かります。一方、通常の偏回帰係数ではその大小から各変数の重要性を判断することはできません。
■偏回帰係数の有意性の検定
偏回帰係数の有意性の検定とは、定数項も含めた各偏回帰係数![]() が0であるかについての検定結果です。帰無仮説は「偏回帰係数=0」です。偏回帰係数
が0であるかについての検定結果です。帰無仮説は「偏回帰係数=0」です。偏回帰係数![]() を標準誤差で割った値について、自由度
を標準誤差で割った値について、自由度![]() のt分布を用いて検定を行います。すなわち、次の式から算出される統計量t(t値)が自由度
のt分布を用いて検定を行います。すなわち、次の式から算出される統計量t(t値)が自由度![]() のt分布に従うことを用います。nはサンプルサイズを、kは説明変数の数を表します。
のt分布に従うことを用います。nはサンプルサイズを、kは説明変数の数を表します。
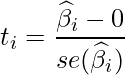
この検定により有意となった場合、偏回帰係数は0ではない、すなわちその説明変数の目的変数に対する影響は統計的に有意であると言うことができます。例えば、年平均気温の偏回帰係数の有意性の検定ではt値は次のように算出されます。
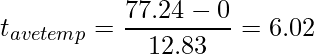
この値が自由度47-4-1=42のt分布に従うことを用いて検定を行います。
■偏回帰係数の信頼区間
偏回帰係数の有意性の検定で用いた自由度![]() のt分布を使うと、次の式から偏回帰係数
のt分布を使うと、次の式から偏回帰係数![]() の
の![]() 信頼区間を求めることができます。nは抽出したサンプルサイズ、kは説明変数の数、
信頼区間を求めることができます。nは抽出したサンプルサイズ、kは説明変数の数、![]() は自由度が
は自由度が![]() のt分布における上側確率が
のt分布における上側確率が![]() となる値(t値)を表します。
となる値(t値)を表します。
例えば、年平均気温の偏回帰係数の95%信頼区間は次のように算出されます。
【コラム】ダミー変数
ダミー変数とは、カテゴリカルデータや2値型データのようなもともと数値でないデータに対して、0と1を用いて数量化した変数のことです。例えば、身長を目的変数![]() 、体重と性別を説明変数
、体重と性別を説明変数![]() として重回帰分析を行う場合に、「男性=0」、「女性=1」として重回帰式を求める場合があります。
として重回帰分析を行う場合に、「男性=0」、「女性=1」として重回帰式を求める場合があります。
例えば上のような重回帰式では、性別![]() に0を代入すると男性の身長を予測するための重回帰式が、性別
に0を代入すると男性の身長を予測するための重回帰式が、性別![]() に1を代入すると女性の身長を予測するための重回帰式が得られます。
に1を代入すると女性の身長を予測するための重回帰式が得られます。
■おすすめ書籍
WEBで公開されているアイスクリーム統計学を書籍化したものです。なんとなく分かりにくい回帰分析と因子分析のイメージを掴むのにぴったりです。
27. 回帰分析
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計解析事例
重回帰分析
- 1. 統計ことはじめ
1-5. 説明変数と目的変数
- 23. 検定の前に
23-6. 両側検定と片側検定
- 24. 平均値の検定
24-1. 母平均の検定(両側t検定)
- ブログ
回帰係数と相関係数
- ブログ
Excelで重回帰分析(1)
- ブログ
重回帰分析ができない








