- Step1. 基礎編
- 27. 回帰分析
27-1. 単回帰分析
回帰とは、目的変数![]() について説明変数
について説明変数![]() を使った式で表すことをいいます(目的変数と説明変数の詳細については1-5章を参照)。この式のことを「回帰方程式」、あるいは簡単に「回帰式」といいます。また、回帰式を求めることを「回帰分析」といいます。
を使った式で表すことをいいます(目的変数と説明変数の詳細については1-5章を参照)。この式のことを「回帰方程式」、あるいは簡単に「回帰式」といいます。また、回帰式を求めることを「回帰分析」といいます。
例題:
次の散布図は都道府県の人口密度と人口10万人あたりの薬局の数を示したものです。薬局の数 ![]() を目的変数、人口密度
を目的変数、人口密度 ![]() を説明変数とするとき、回帰式を求めるとどのようになるでしょうか。
を説明変数とするとき、回帰式を求めるとどのようになるでしょうか。
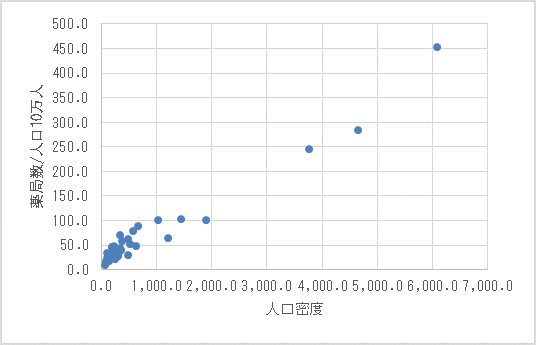
出典:総務省統計局 社会生活統計指標-都道府県の指標-2015
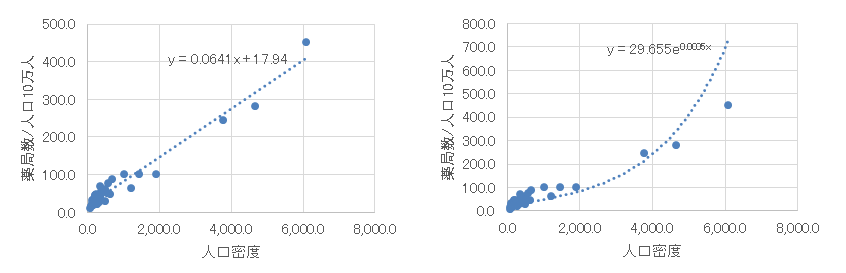
次の2つの図は散布図上に回帰式を描いたものです。このように、データに対しては様々な回帰式を求めることができます。この章では、左側の図のように ![]() (
(![]() は切片、
は切片、![]() は傾きを表します)という一次関数で表される回帰式について説明します。
は傾きを表します)という一次関数で表される回帰式について説明します。
回帰式 ![]() には、説明変数
には、説明変数 ![]() が1つだけ用いられています。このような式を「単回帰式」といい、単回帰式を求めることを「単回帰分析」といいます。一方、説明変数を複数使った回帰式を求めることもできます。このような式を「重回帰式」といい、重回帰式を求めることを「重回帰分析」といいます。
が1つだけ用いられています。このような式を「単回帰式」といい、単回帰式を求めることを「単回帰分析」といいます。一方、説明変数を複数使った回帰式を求めることもできます。このような式を「重回帰式」といい、重回帰式を求めることを「重回帰分析」といいます。
■単回帰式 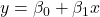 における
における 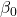 と
と 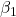 の求め方
の求め方
今考えようとしている ![]() は、薬局の数
は、薬局の数 ![]() を人口密度
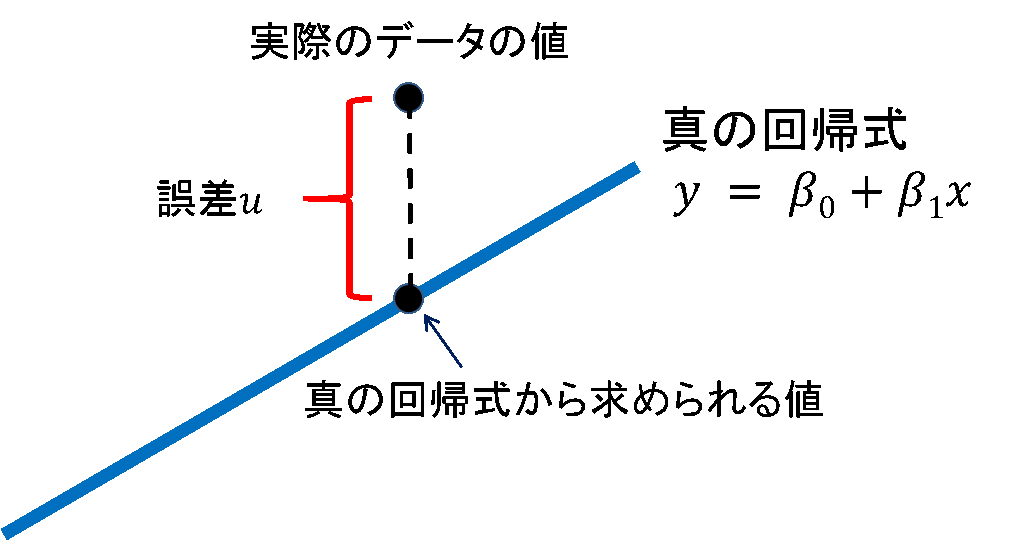
を人口密度 ![]() の式で表した“真の”(あるいは理論的な)単回帰式です。しかしながら、実際のデータには測定誤差など様々な誤差を含んでいると考えられることから、次のような回帰式を考えます。
の式で表した“真の”(あるいは理論的な)単回帰式です。しかしながら、実際のデータには測定誤差など様々な誤差を含んでいると考えられることから、次のような回帰式を考えます。
![]() は「誤差」で、「真の回帰式から実際のデータまでのズレ」を表すものとします。
は「誤差」で、「真の回帰式から実際のデータまでのズレ」を表すものとします。
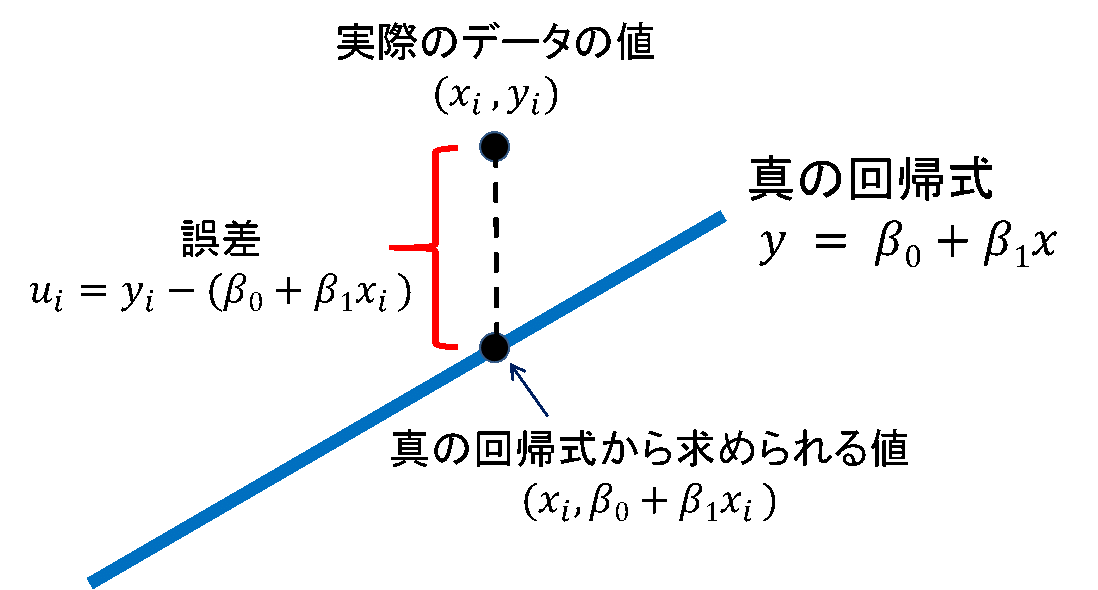
単回帰分析における ![]() と
と ![]() は、すべてのデータの誤差
は、すべてのデータの誤差 ![]() が小さくなるように定まります。例えば実際のデータが
が小さくなるように定まります。例えば実際のデータが ![]() 個ある場合に、
個ある場合に、![]() 番目の値を(
番目の値を(![]() ,
, ![]() )とすると、真の回帰式から求められる値は(
)とすると、真の回帰式から求められる値は(![]() ,
, ![]() )となります。これらを用いると、誤差
)となります。これらを用いると、誤差 ![]() は次のように求められます。
は次のように求められます。
ただし、真の回帰式 ![]() の
の ![]() と
と ![]() は神のみぞ知る値であり、直接求めることはできません。そこで、実際のデータを使って
は神のみぞ知る値であり、直接求めることはできません。そこで、実際のデータを使って ![]() (
(![]() の推定値)と
の推定値)と ![]() (
(![]() の推定値)を推定することを考えます。次の式で表される
の推定値)を推定することを考えます。次の式で表される ![]() の二乗和を考え、この二乗和が最小となるように
の二乗和を考え、この二乗和が最小となるように ![]() と
と ![]() を算出します。この方法を「最小二乗法」といいます。
を算出します。この方法を「最小二乗法」といいます。
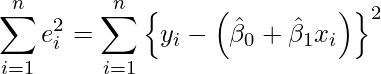
![]() は「残差」とよばれるもので、人口密度のデータを回帰式に代入して得られた値と、実際の薬局の数のデータとの差を表します。誤差
は「残差」とよばれるもので、人口密度のデータを回帰式に代入して得られた値と、実際の薬局の数のデータとの差を表します。誤差 ![]() とは異なるので注意が必要です。誤差と残差のちがいについては27-4章をご覧ください。
とは異なるので注意が必要です。誤差と残差のちがいについては27-4章をご覧ください。
最小二乗法により推定された ![]() と
と ![]() は「偏回帰係数」と呼ばれます。これらは実際のデータから算出された推定値であり、真の回帰式における
は「偏回帰係数」と呼ばれます。これらは実際のデータから算出された推定値であり、真の回帰式における ![]() と
と ![]() とは異なることから「^(ハット)」をつけて表します。例題のデータから推定された単回帰式は、
とは異なることから「^(ハット)」をつけて表します。例題のデータから推定された単回帰式は、![]() を人口10万人あたりの薬局の数の推定値、
を人口10万人あたりの薬局の数の推定値、![]() を人口密度とすると次のようになります。
を人口密度とすると次のようになります。
また、![]() と
と ![]() はそれぞれ次のようになります。
はそれぞれ次のようになります。
この回帰式の ![]() は実際のデータではなく、回帰式から算出される推定値であることから「
は実際のデータではなく、回帰式から算出される推定値であることから「![]() 」と表します。偏回帰係数
」と表します。偏回帰係数 ![]() は
は ![]() (人口密度)が1増加したときに
(人口密度)が1増加したときに ![]() (薬局の数)がどれだけ増加/減少するかを表す値です。
(薬局の数)がどれだけ増加/減少するかを表す値です。
【コラム1】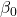 と
と 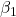 の求め方
の求め方
最小二乗法を用いて回帰式 ![]() の
の ![]() と
と ![]() を定める場合、次の式を
を定める場合、次の式を ![]() と
と ![]() それぞれで偏微分した式を0とした2つの式を使います。
それぞれで偏微分した式を0とした2つの式を使います。
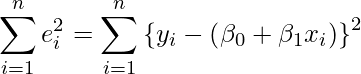
2つの式は煩雑なためここでは記述を省略しますが、整理することで次のように ![]() と
と ![]() を求める式を導くことができます。
を求める式を導くことができます。
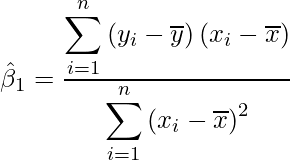
【コラム2】誤差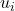 の仮定
の仮定
回帰モデルを考えるにあたって、誤差 ![]() にはいくつかの仮定している条件があります。
にはいくつかの仮定している条件があります。
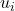 の期待値は0である:
の期待値は0である: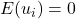
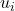 の分散は常に
の分散は常に 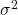 である:
である: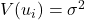
- 異なる誤差
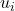 、
、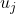 は互いに独立である:
は互いに独立である:
- 誤差
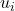 は正規分布に従う
は正規分布に従う
これらの条件から、![]() は互いに独立に同一の正規分布
は互いに独立に同一の正規分布 ![]() に従うと仮定されます。
に従うと仮定されます。
【コラム3】回帰にまつわる用語
- 回帰の現象(平均への回帰)
データを繰り返し測定すると、1回目の測定で高かったり低かったりした値は、2回目の測定ではより全体の平均に近づいた値として観測される現象のことです。例えば、1回目の血圧測定で高めの値が出た人に対して2回目の測定を行うと、血圧測定した集団の平均値に近づいた値になる可能性が高いことが知られています。
- 回帰の錯誤(回帰の誤謬)
回帰の現象が観察された場合に、対象者に行われた処置や対応による効果であると誤って判断してしまうことを指します。例えば、1回目の血圧測定で高めの値が出た人に対して「ゆっくりと深呼吸するように」と指摘したことによって、2回目の測定では血圧が下がったと誤った判断を行ってしまう場合があります。このような判断を回帰の錯誤といい、本来であればこのような判断を行うためにはより慎重な検証が必要となります。
■おすすめ書籍
漫画ですが、ある程度の基礎知識が要求されます。それでも、この1冊を読み込めば回帰分析とはなんぞやというのが分かるようになります。
27. 回帰分析
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 1. 統計ことはじめ
1-5. 説明変数と目的変数
- 26. 相関分析
26-1. 散布図








