- Step1. 基礎編
- 27. 回帰分析
27-2. 最小二乗法
27-1章で学んだように、回帰分析では偏回帰係数を最小二乗法を用いて算出します。この章では偏回帰係数の実際の求め方について学びます。
最小二乗法を用いて回帰式![]() の
の![]() と
と![]() を定める場合、次の式を
を定める場合、次の式を![]() と
と![]() それぞれで偏微分した式を0とした2つの式を使います。
それぞれで偏微分した式を0とした2つの式を使います。
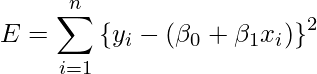
![]() で偏微分すると、
で偏微分すると、
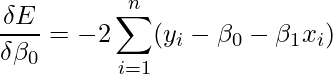
となり、![]() で偏微分すると、
で偏微分すると、
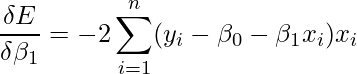
となります。これらの式を0とすると、次のような式が得られます。
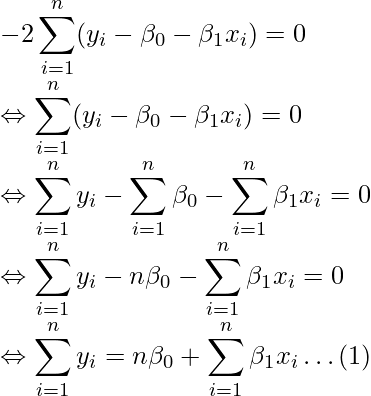
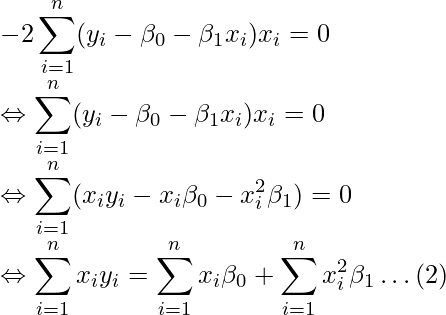
これら(1)(2)の式(正規方程式とよばれることがあります)を整理することで、![]() と
と![]() の推定値である
の推定値である![]() と
と![]() を求める式を導くことができます。
を求める式を導くことができます。
(1)の式を変形すると
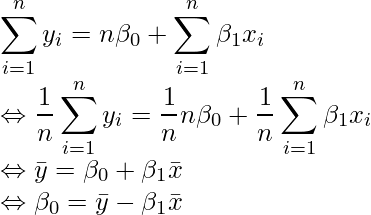
となります。![]() 、
、![]() から
から![]() と
と![]() を得ます。
を得ます。
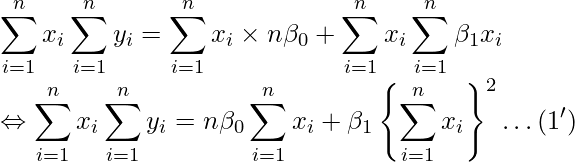
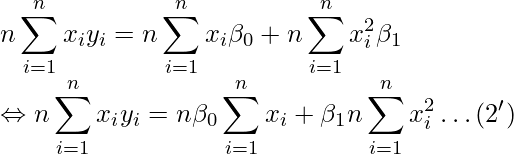
(2')-(1')を計算すると、
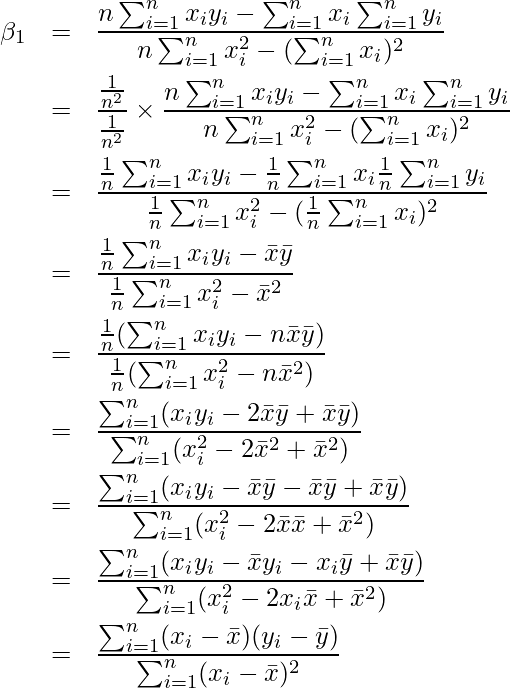
となります。したがって、![]() と
と![]() を求める式は次のようになります。
を求める式は次のようになります。
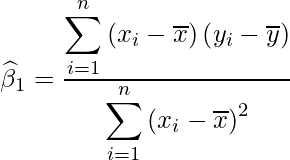
![]() は次のように書くこともできます。
は次のように書くこともできます。
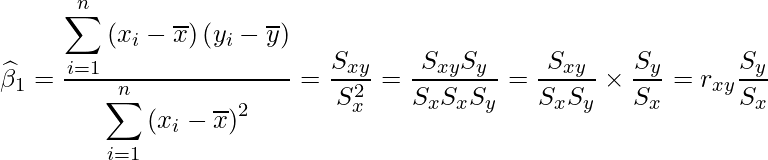
ただし、![]() は
は![]() と
と![]() の共分散を、
の共分散を、![]() は
は![]() の分散を、
の分散を、![]() は
は![]() の分散を、
の分散を、![]() は
は![]() と
と![]() の相関係数を表します。
の相関係数を表します。
■回帰式の特徴
- 推定値
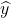 の平均値は、実際の観測値
の平均値は、実際の観測値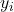 の平均と等しい
の平均と等しい - 回帰直線は
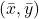 を通る
を通る
(1)の両辺を![]() で割ると
で割ると
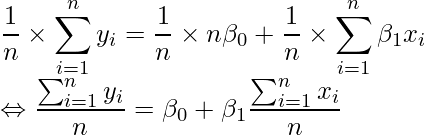
となり、観測値![]() の平均値(左辺)と推定値
の平均値(左辺)と推定値![]() の平均値(右辺)が等しくなることが分かります。
の平均値(右辺)が等しくなることが分かります。
(1)の式![]() と回帰式
と回帰式![]() を使って
を使って
を得ます。この式から、![]() のとき、
のとき、![]() となることが分かります。
となることが分かります。






