27-5章のデータを用いてエクセル統計で重回帰分析を行った場合の出力について解説します。

■回帰式の精度

回帰式の精度は「自由度調整済み決定係数」から確認できることは27-4章で既に学びました。エクセル統計では決定係数の「修正R2乗」に出力されます。このデータでは0.6121となっており、目的変数を説明変数によって6割程度説明できるということを示しています。

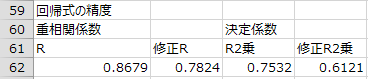
実際のデータと回帰式から求められた予測値との相関係数を「重相関係数R」といいます。また、説明変数の数の割合が多くなるほど重相関係数の値は過大評価されやすいため、この点を調整したものを「自由度調整済み重相関係数（修正R）」といいます。決定係数は重相関係数の2乗に等しくなります。

■回帰式の有意性（分散分析）

回帰式の有意性は、データから算出された回帰式が統計的に意味のあるものか（説明変数が目的変数を説明しているか）を検定した結果です。帰無仮説は「回帰変動は0である（偏回帰係数はすべて0である）」です。この検定は分散分析によって行われますが、分散分析とF分布の詳細については28章以降で詳しく触れます。

結果を見るとP値=0.027となっており、有意水準5%で帰無仮説は棄却されます。したがって、この回帰式による回帰変動は0ではない＝すべての偏回帰係数は0ではない＝この回帰式は統計的に意味があると結論付けられます。

■回帰式に含まれる変数

勝利数を目的変数とし、説明変数のうち打率を、得点を、失点を、防御率をとすると、推定された重回帰式を次のように書くことができます。

標準偏回帰係数を見ると、目的変数に対して正の影響をもつ（説明変数が増加すれば目的変数も増加する）説明変数は「打率」、「得点」、「失点」であるのに対し、負の影響をもつ（説明変数が増加すると目的変数は減少する）説明変数は「防御率」であることが分かります。また、目的変数に対して最も大きな影響をもつものは、標準偏回帰係数の絶対値が最も大きい「防御率」となります。ただし、目的変数に対して統計的に有意な影響を持つ説明変数は無いという結果になりました。

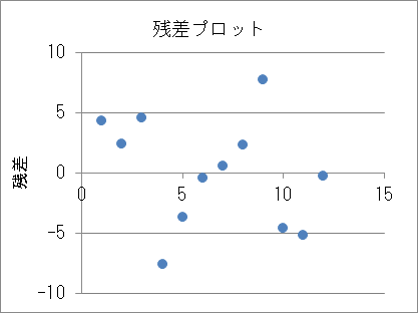
■残差プロット

残差は縦軸0を中心に均等に散らばっているように見えます。また、外れ値も無さそうです。

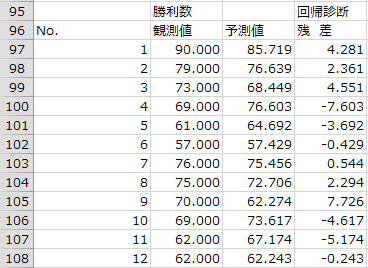
■予測値と残差

「観測値」は重回帰分析の目的変数として用いた実際のデータです。「予測値」は、推定された回帰式に説明変数の値を代入して算出した目的変数の推定値です。これらの差、すなわち観測値から予測値を引いたものが「残差」です。この残差の値を使った残差プロットが作成されます。