- 26. 相関分析
練習問題（26. 相関分析）
1
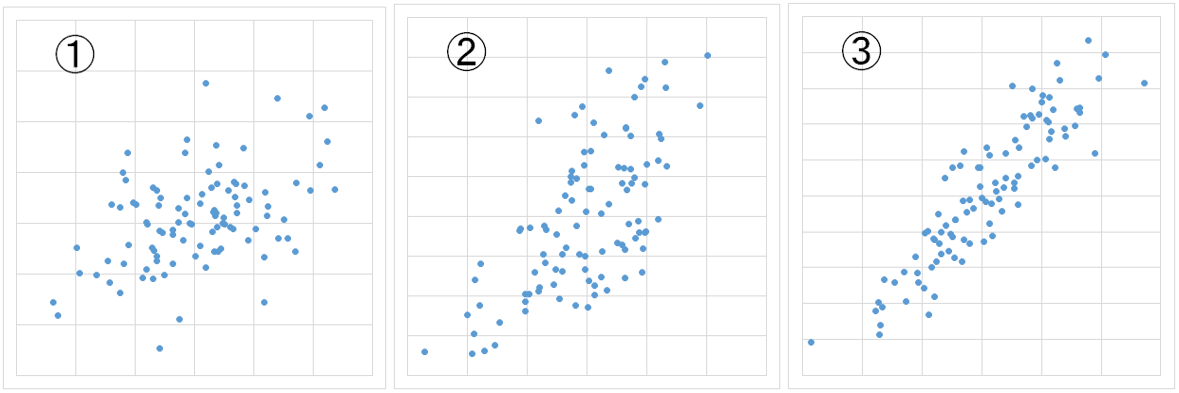
次の3つの散布図のうち、相関係数の絶対値が一番大きいものはどれか。
答えを見る
- 答え
閉じる -
答えは3です。
一般に相関係数の絶対値が大きい場合、散布図からはより直線的な傾向が見られるようになります。上の図における相関係数は1から順にそれぞれ0.45、0.66、0.90となっていて、相関係数が高い散布図の方がより直線的に点が並んでいるのが読み取れます。
2
相関係数について述べられた次の文章のうち、正しいものを選べ。
- サンプルサイズが半分になると、相関係数も半分の値になる。
- 相関係数が高い変数の間には因果関係があると考えられる。
- 相関係数0.5と相関係数-0.9のデータでは、後者の方が値が小さいため関連性はなさそうだと言える。
- 相関係数は、その値の絶対値が大きいほうが、関連性が高いことを表している。
答えを見る
- 答え閉じる
-
- ×：相関係数は、サンプルサイズに依存する数値ではありません。
- ×：相関係数は、因果関係を表す指標ではありません。
- ×：相関係数は-1から1までの値を取り、0が無相関で絶対値が大きくなるほど（0から離れるほど）関連性が高いことを表します。
- ◯：正しいです。
3
相関係数と偏相関係数について述べられた次の文章のうち、正しいものを選べ。
- 相関係数は絶対値が1以下にならない場合がある。
- 第3の変数の影響によって、2つの変数間の相関係数が見かけ以上に大きくなることはあるが、見かけ上無相関になることもある。
- 偏相関係数を求めることで、2つの変数間の因果関係が推測できる。
- 相関係数と偏相関係数の正負は必ず一致する。
答えを見る
- 答え閉じる
-
- ×：相関係数の絶対値は1以下となります。
- ◯：正しいです。第3の変数の影響があることによって、2つの変数間が見かけ上は無相関になることもあります。これを「疑似無相関」といいます。
- ×：偏相関係数から因果関係を推測することはできません。
- ×：26-4章のように、相関係数と偏相関係数の正負は逆転することがあります。
4
答えを見る
- 答え閉じる
-
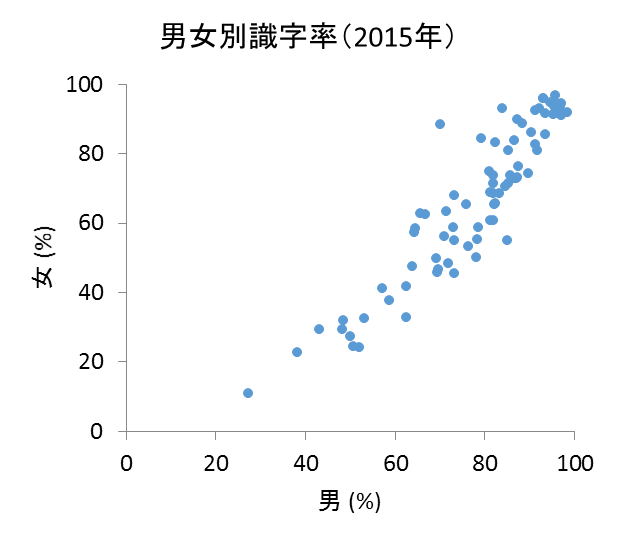
まず、男性の識字率が高い国ほど女性の識字率が高いということが読み取れます。相関係数を計算すると0.94になります。これを結論としてもよいですが、もう少し詳しく見てみることもできます。
例えば、男女の識別率は世界の地域によって傾向が異なることが予想されます。そこで、「アジア」「南北アメリカ」「アフリカ」の3つに分けて散布図を描いてみます。
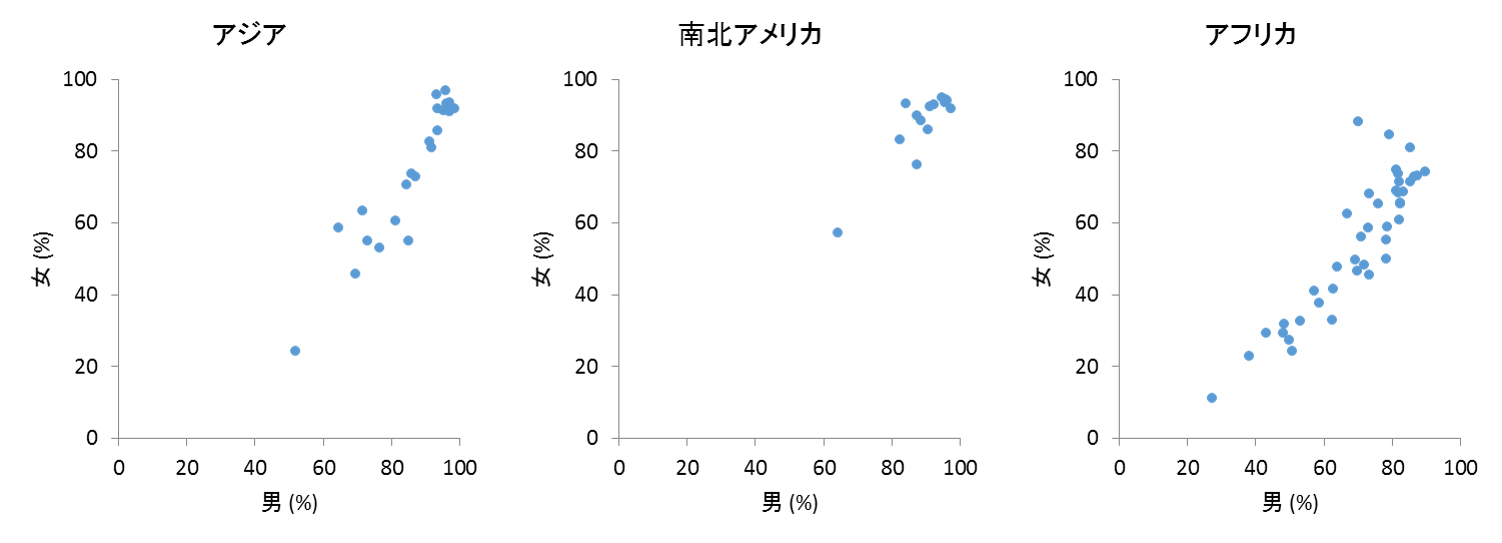
この散布図を見ると、「アジアでは男性の識字率は比較的高い」、「南北アメリカでは男女ともに識字率が高い」、「アフリカでは国によって識字率に大きな差がある」といったことが読み取れます。
5
ある2種類の果実種（品種A、品種B）について、生育時の平均日照時間と果実の重量をプロットしたところ、次の図1のようになった。なお、この相関係数は0.19である。次に、果実種で層別しプロットすると図2のようになり、品種Aの相関係数は0.68で、品種Bの相関係数は0.74であった。これらの散布図について述べられた次の文章から、正しいものを選べ。
- 層別の有無にかかわらず正の相関がみられるので、層別する必要はない。
- 品種A、品種Bのどちらも平均日照時間と果実の重量に高い相関があると言える。
- 品種A、品種Bのどちらも、日照時間を増やせば果実の重量が重くなると言える。
答えを見る
- 答え閉じる
-
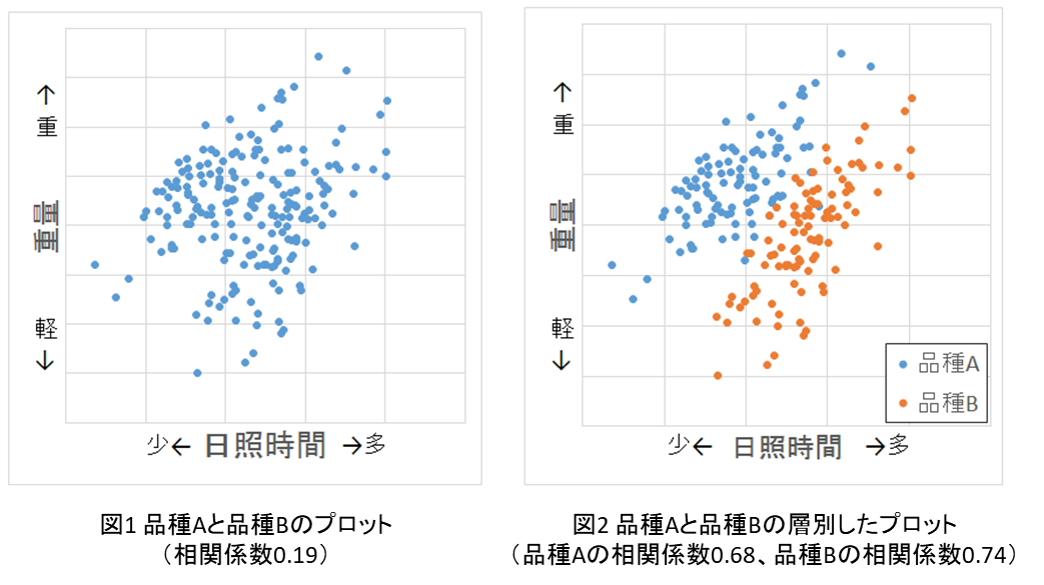
- ×：層別によらず相関係数の符号が等しいことは、層別自体を行うことの判断理由とはなりません。
- ◯：正しいです。
- ×：この散布図は品種別で日照時間と果実の重量に正の相関があるという関係を読み取ることはできますが、日照時間を長くすれば重量が増えるという因果関係を読み取ることはできません。
