2016年11月統計検定2級の問題の解説(その1)
2017/06/16
カテゴリ:統計検定
※統計検定2級 解説記事一覧はこちら※
2016年11月に実施された統計検定2級の問題の解説をしています。
この記事では、次の6問の解説をしています。下のリストからクリック、またはタップした問題の解説部分へジャンプします。
問1(回答番号1,2)
■回答番号1
幹葉図から読み取れる情報について、各選択肢の正誤は次の通りです。
 誤:最高点は92点ではなく90点です。
誤:最高点は92点ではなく90点です。 誤:最低点は56点ではなく40点です。
誤:最低点は56点ではなく40点です。 正:60点未満の点数を数えると、40点が1人、56点が1人、58点が5人の合計7人です。
正:60点未満の点数を数えると、40点が1人、56点が1人、58点が5人の合計7人です。 誤:上位5人の点数は上から90点、82点、80点、78点、78点であるため、78点が必要です。
誤:上位5人の点数は上から90点、82点、80点、78点、78点であるため、78点が必要です。 誤:最頻値は70点ではなく58点です。
誤:最頻値は70点ではなく58点です。
■回答番号2
データが25個で奇数ですから、中央値は上から(あるいは下から)数えて13番目のデータの点数です。
問2(回答番号3,4)
■回答番号3
ヒストグラムを選択するため、度数分布表の空欄を埋めます。度数分布表と問題文の記述内容から、次のようなことが分かります
夏季の合計度数428から数値が分かっているものを引くと、「(ウ)+(エ)=26」となります。同様に冬季についても計算すると、「(オ)+(カ)=217」となります。
また、「日平均気温が10℃を超える日が112日である」という条件から、「(カ)+35=112」とわかります。
さらに、「期間全体で2番目に大きい度数は144である」という条件から、「(ア)か(イ)のどちらかが144」とわかります。
まとめると、次の4つの条件があることがわかります。
- (ア)か(イ)のどちらかが144
- (ウ)+(エ)=26
- (オ)=140
- (カ)=77
まず、条件1について考えます。仮に(ア)が144だとすると、条件2より「(ウ)=4」、「(エ)=22」です。また、「(イ)=99」となります。
もし(イ)が144だとすると、「(エ)+77=144」つまり「(エ)=67」となるのですが、これは条件2と矛盾します。よって、(ア)が144でなければならないことがわかります。
以上の事から、度数は下の階級から順に![]() となります。これに対応するヒストグラムは
となります。これに対応するヒストグラムは![]() です。
です。
■回答番号4
度数分布表とヒストグラムより読み取れる情報について、各選択肢の正誤は次の通りです。
 正:ヒストグラムから、峰が2つあることが読み取れます。
正:ヒストグラムから、峰が2つあることが読み取れます。 正:10℃以下の2階級の度数は合計で194、15℃以下の3階級の度数の合計は293ですから、12.5度以下となるもの194~293の間にあると考えられます。
正:10℃以下の2階級の度数は合計で194、15℃以下の3階級の度数の合計は293ですから、12.5度以下となるもの194~293の間にあると考えられます。 誤:10℃を超えて25℃以下の3階級の度数は合計で406となり、全体の50%よりも多いことが分かります。
誤:10℃を超えて25℃以下の3階級の度数は合計で406となり、全体の50%よりも多いことが分かります。 正:もっとも度数の高い階級は「20℃より高く25度以下」であるため、その代表値は「
正:もっとも度数の高い階級は「20℃より高く25度以下」であるため、その代表値は「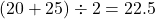 」です。
」です。 正:もっとも度数の高い階級と2番目に高いものの度数の合計は317です。「
正:もっとも度数の高い階級と2番目に高いものの度数の合計は317です。「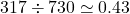 」となり、全体の40%よりも多いことが分かります。
」となり、全体の40%よりも多いことが分かります。
問3(回答番号5,6)
■回答番号5
(ア)、(イ)に当てはまるものが「平均、中央値、最頻値」のうちのいずれかです。しかし、ヒストグラムの形状よりどちらも最頻値でないことが分かります。また、このヒストグラムの形状は「右に裾が長い(裾を引く)」と言えます。このような形状の場合は一般に「最頻値<中央値<平均値」の関係が成り立ちます。よって、正しい選択肢は![]() です。
です。
■回答番号6
ヒストグラムから読み取れる情報について、各記述の正誤は次の通りです。
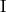 誤:200万円未満までの累積相対度数は20.6%となり、これ以下の階級には第一四分位数が存在しないことが分かります。
誤:200万円未満までの累積相対度数は20.6%となり、これ以下の階級には第一四分位数が存在しないことが分かります。 正:第一四分位数は「200万円以上~300万円未満」、第三四分位数は「700万円以上~800万円未満」です。四分位範囲が最も大きくなる時は「
正:第一四分位数は「200万円以上~300万円未満」、第三四分位数は「700万円以上~800万円未満」です。四分位範囲が最も大きくなる時は「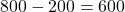 」、反対に最も小さくなる時が「
」、反対に最も小さくなる時が「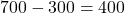 」と考えられます。
」と考えられます。 正:この分布は右に裾が長い形状をしています。
正:この分布は右に裾が長い形状をしています。
問4(回答番号7,8)
■回答番号7
「得点」と「勝点」の散布図はいちばん左側の図です。これを見ると非常に相関が高いと考えられます。選択肢の中で最も妥当なのは![]() の0.87です。相関係数ごとの散布図の様子は、統計学の時間26章の練習問題も参考にしてください。
の0.87です。相関係数ごとの散布図の様子は、統計学の時間26章の練習問題も参考にしてください。
■回答番号8
3つの散布図から読み取れる情報について、各記述の正誤は次の通りです。
 正:一番右の散布図を見ると、もっとも得点が多かったチーム(一番右側の点)よりY(失点)の小さいチームはなかったことが分かります。
正:一番右の散布図を見ると、もっとも得点が多かったチーム(一番右側の点)よりY(失点)の小さいチームはなかったことが分かります。 正:得点と失点の相関はいちばん右の散布図が対応します。この形状から、左の二つの散布図よりも散らばりが大きく、相関が低いことが分かります。
正:得点と失点の相関はいちばん右の散布図が対応します。この形状から、左の二つの散布図よりも散らばりが大きく、相関が低いことが分かります。 誤:散布図より、得点の範囲はおよそ50程度、失点の範囲はおよそ35程度であることから、得点の範囲の方が大きいことが分かります。
誤:散布図より、得点の範囲はおよそ50程度、失点の範囲はおよそ35程度であることから、得点の範囲の方が大きいことが分かります。
問5(回答番号9,10)
■回答番号9
調査について、各記述の正誤は次の通りです。
 誤:このような調査票の配布の仕方では、サンプルの代表性が低くなる場合や偏りが発生する場合が考えられます。
誤:このような調査票の配布の仕方では、サンプルの代表性が低くなる場合や偏りが発生する場合が考えられます。 誤:恣意的に回答を誘導するような質問は、回答が偏ってしまうことがあります。
誤:恣意的に回答を誘導するような質問は、回答が偏ってしまうことがあります。 誤:質問文を読み解くのが難しくなると回答者の負担となり、回答拒否となる場合があります。
誤:質問文を読み解くのが難しくなると回答者の負担となり、回答拒否となる場合があります。
■回答番号10
層別抽出の説明として、各選択肢の正誤は次の通りです。
 誤:層内が母集団構成に近くとも、層別による効果が高くなりません。
誤:層内が母集団構成に近くとも、層別による効果が高くなりません。 正:層内が等質であれば、層別の効果が高くなります。
正:層内が等質であれば、層別の効果が高くなります。 誤:層内が異質である場合、層別の効果は高くなりません。
誤:層内が異質である場合、層別の効果は高くなりません。 誤:層のサイズや数は直接的には関係ありません。
誤:層のサイズや数は直接的には関係ありません。 誤:層のサイズや数は直接的には関係ありません。
誤:層のサイズや数は直接的には関係ありません。
問6(回答番号11)
■回答番号11
フィッシャーの3原則については、統計学の時間31章の記事を参照してください。
2016年11月問題の解説
- その1:問1~問6(本記事)








