2016年11月統計検定2級の問題の解説(その2)
2017/06/16
カテゴリ:統計検定
※統計検定2級 解説記事一覧はこちら※
2016年11月に実施された統計検定2級の問題の解説をしています。
この記事では、次の6問の解説をしています。下のリストからクリック、またはタップした問題の解説部分へジャンプします。
問7(回答番号12,13)
■回答番号12
「●型の人を正しく●型と言い当てる確率」をそれぞれ4つの血液型に対して計算し、和を取ったものが答えです。
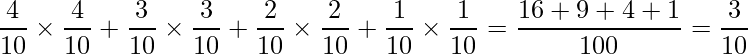
■回答番号13
求める確率は、次のような条件付き確率です。
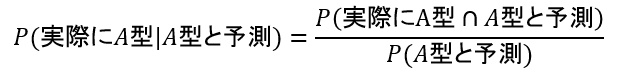
分子は、「A型の人がA型であると予測される確率」です。この確率は次のように求められます。

分母は、「A/B/O/AB型の人がA型であると予測される確率」です。問題文より、A型でない人がA型と予測される確率は![]() であることから、この確率は次のように求められます。
であることから、この確率は次のように求められます。
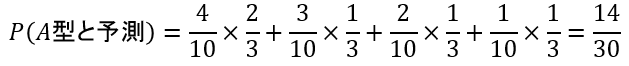
以上の事から、次のように求めることができます。

問8(回答番号14,15)
■回答番号14
問題から、![]() は全て標準化されているということから、
は全て標準化されているということから、
であることが分かります。また、![]() と
と![]() の相関係数
の相関係数![]() は、相関係数の定義より
は、相関係数の定義より
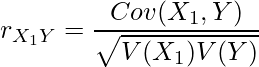
となるので、![]() と
と![]() が分かれば求めることができます。
が分かれば求めることができます。
まず、![]() を求めます。
を求めます。![]() であるので、
であるので、![]() は
は
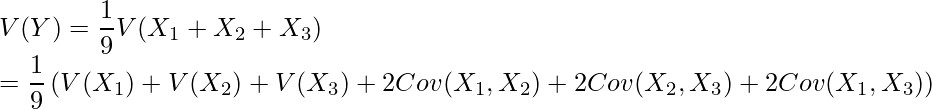
と変形できます。ここで、![]() が互いに無相関であることから、
が互いに無相関であることから、![]() となります。これを代入すると、
となります。これを代入すると、
となります。次に![]() を求めます。
を求めます。
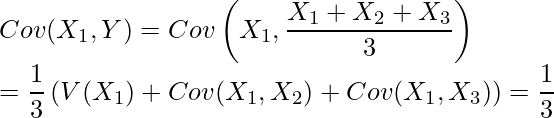
以上の事から、![]() は次のようになります。
は次のようになります。
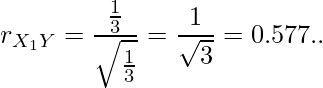
■回答番号15
前問と同様に、![]() を求めれば解けます。最初に、
を求めれば解けます。最初に、![]() は前問の通り
は前問の通り
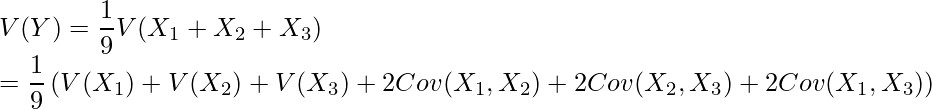
と変形できますが、それぞれの![]() 同士の相関係数が0.5であることから、
同士の相関係数が0.5であることから、![]() となることが違います。これを代入すると次のようになります。
となることが違います。これを代入すると次のようになります。
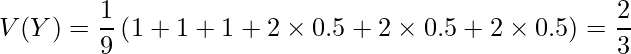
![]() についても同様に
についても同様に
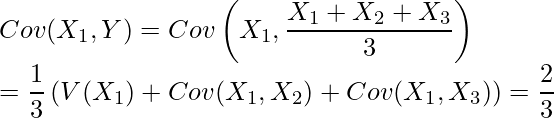
となります。以上の事から、求める相関係数は
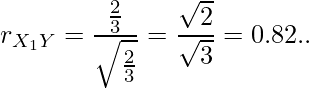
問9(回答番号16,17,18)
■回答番号16
パラメータ![]() のポアソン分布の平均と分散は
のポアソン分布の平均と分散は![]() となります。
となります。
■回答番号17
イベント参加人数を確率変数![]() とおくと、求める確率は
とおくと、求める確率は![]() です。問題文から、
です。問題文から、![]() は正規分布に従うと見なせることから
は正規分布に従うと見なせることから
と考えられます。よって、求める確率は
となり、標準正規分布表からZ=1.41の上側確率を参照すると、0.079であることが分かります。
■回答番号18
問題文より、景品を用意する個数![]() について、
について、![]() となるような
となるような![]() を求めればよいことが分かります。問題文より、
を求めればよいことが分かります。問題文より、![]() は正規分布に従うことから、
は正規分布に従うことから、
と考えられます。
となりますが、この確率が0.05になるようなZを標準正規分布表から探してくると、Z=1.64となります。よって、
となります。
問10(回答番号19,20)
■回答番号19
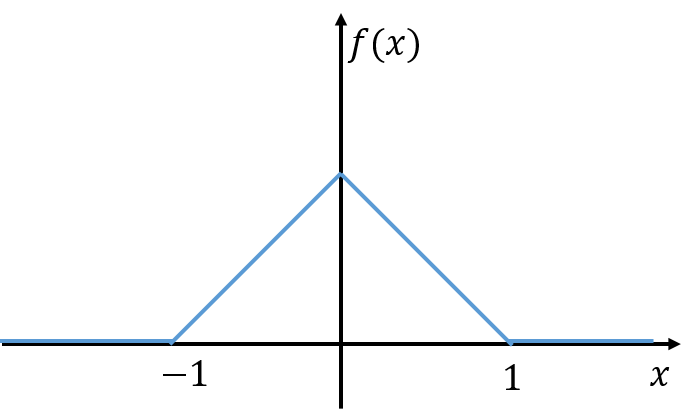
![]() は次のような形の関数です。
は次のような形の関数です。![]() を中心にした左右対称な三角形の形状をしていることが分かります。
を中心にした左右対称な三角形の形状をしていることが分かります。
まず、期待値![]() を計算します。
を計算します。
![Rendered by QuickLaTeX.com \displaytyle \int_{-1}^{0} x(x+1)dx + \int_{0}^{1} x(-x+1)dx = \left[ \frac{x^3}{3}+ \frac{x^2}{2} \right]_{-1}^{0} + \left[ - \frac{x^3}{3} + \frac{x^2}{2} \right]_{0}^{1} \\ = \left( 0+0 \right) - \left( - \frac{1}{3} +\frac{1}{2} \right) + \left( - \frac{1}{3}+ \frac{1}{2} \right) - \left( 0+0 \right) =0](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-225da11d5ef9453417aee6f791c09b30_l3.png)
![]() で左右対称であるため、直観的に
で左右対称であるため、直観的に![]() と求めても大丈夫です。ただし、コーシー分布などの場合はこの方法が使えないことに注意しましょう。
と求めても大丈夫です。ただし、コーシー分布などの場合はこの方法が使えないことに注意しましょう。
次に、分散を計算します。![]() であることから、
であることから、![]() となる事を用います。
となる事を用います。
![Rendered by QuickLaTeX.com \displaytyle \int_{-1}^{0} x^2(x+1)dx + \int_{0}^{1} x^2(-x+1)dx = \left[ \frac{x^4}{4}+ \frac{x^3}{3} \right]_{-1}^{0} + \left[ - \frac{x^4}{4} + \frac{x^3}{3} \right]_{0}^{1} \\ = \left( 0+0 \right) - \left( \frac{1}{4} - \frac{1}{3} \right) + \left( - \frac{1}{4}+ \frac{1}{3} \right) - \left( 0+0 \right) = \frac{1}{12}+ \frac{1}{12} =\frac{1}{6}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-8b57cc48fbafa28d134929f1a6f5beec_l3.png)
■回答番号20
第一四分位数は、累積分布関数を![]() とすると
とすると![]() となる
となる![]() です。今回の分布では、
です。今回の分布では、![]() に対して左右対称であることから、
に対して左右対称であることから、![]() の範囲のみで考えてよいことが分かります。
の範囲のみで考えてよいことが分かります。
![]() の
の![]() での累積分布関数は次の通りです。
での累積分布関数は次の通りです。
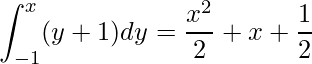
これが0.25となればよいので、次の方程式を解けばよいことが分かります
これは二次方程式であるため解は二つあり、次のようになります。
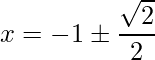
しかし、![]() は-1よりも小さいため、不適であることが分かります。以上の事から、
は-1よりも小さいため、不適であることが分かります。以上の事から、![]() が求める第一四分位数となります。
が求める第一四分位数となります。
問11(回答番号21,22)
■回答番号21
この問題は、期待値と分散の関係式を使うと簡単に解けます。
よって、![]() は次のようになります。
は次のようになります。
■回答番号22
まず(ア)について、![]() の不偏推定量のひとつは不偏分散が考えられます。この時点で、選択肢は2つに絞られることが分かります。次に
の不偏推定量のひとつは不偏分散が考えられます。この時点で、選択肢は2つに絞られることが分かります。次に![]() についてですが、標本平均の二乗
についてですが、標本平均の二乗![]() の期待値
の期待値![]() を考えてみます。
を考えてみます。
前問と同様に、期待値と分散の関係式を使います。
![]() については、次の関係を用います。
については、次の関係を用います。
独立な確率変数![]() があり、期待値は
があり、期待値は![]() で分散は
で分散は![]() であるとき、その標本平均
であるとき、その標本平均
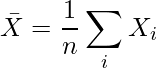
の期待値と分散はそれぞれ次のようになる。
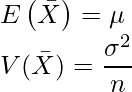
これを用いると、![]() は
は
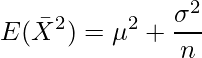
となることが分かります。![]() そのままでは、
そのままでは、![]() の不偏推定量にはなりません。ここで、
の不偏推定量にはなりません。ここで、![]() の不偏推定量である
の不偏推定量である![]() を用いて
を用いて![]() の不偏推定量を構成することを考えます。
の不偏推定量を構成することを考えます。
ある定数![]() を用いて、
を用いて、![]() と
と![]() の和を作ると、次のようになります。
の和を作ると、次のようになります。
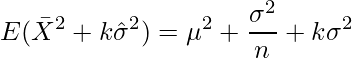
これが![]() となるようなkの値を求めると、
となるようなkの値を求めると、![]() となります。以上の事から、
となります。以上の事から、
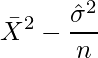
という推定量が、![]() の不偏推定量となります。
の不偏推定量となります。
2016年11月問題の解説
- その2:問7~問11(本記事)








