共分散分析─エクセル統計による解析事例
2017/04/19
カテゴリ：解析事例
タグ：
※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。
分析データ
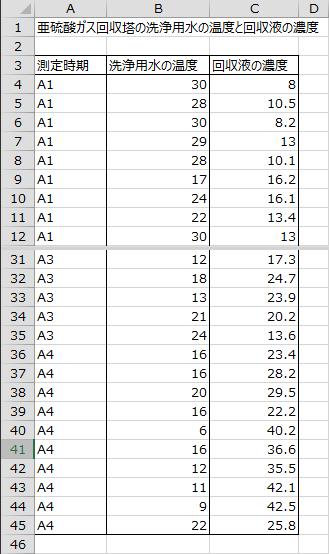
下図は、亜硫酸ガス回収塔の洗浄用水の温度と回収液の濃度を記録したデータです。エクセル統計を用いて共分散分析を行い、測定期間によって回収液の濃度が異なるかどうかを分析してみます。（出典：「多変量解析法《改訂版》」日科技連）
分析手順
測定期間によって回収液の濃度が異なるかどうかは、測定期間ごとに回収液の濃度を目的変数、洗浄用水の温度を説明変数とする回帰直線を作成したときの切片が互いに異なるかどうかによって判断することができます。これには、測定期間ごとの回帰直線が交わらずに平行であり、しかも回帰直線の傾きがいずれも0ではないという前提条件が満たされている必要があります。
そのため、共分散分析は、まず回帰直線の平行性の検定を行ったあと、回帰直線の有意性の検定（傾きが0ではないことを調べる検定）を行い、最後に分散分析表によって回帰直線の切片が異なるかどうかを確認します。
■ 回帰直線の平行性の検定
ダイアログの設定
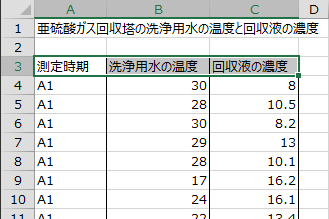
下図のように表の先頭行「A3:C3」を選択します。メニューより［エクセル統計］→［分散分析・多重比較］→［共分散分析］を選択します。
［変数］タブ
ダイアログが表示される際、セル範囲「A3:C45」が［データ入力範囲］に自動で指定されます。「回収液の濃度」を［目的変数］に、「測定時期」を［固定因子］に、「洗浄用水の温度」を［共変量］にセットします。
［モデル］タブ
［モデル］タブで［因子］の中の「固 測定時期」と「共 洗浄用水の温度」を選択し、「指定する因子」から「交互作用」を選択して［モデルに追加］をクリックします。交互作用項をモデルに入れることで、「測定時期」と「洗浄用水の温度」の交互作用、すなわち測定時期ごとの回帰直線の平行性を確認することができます。
出力内容
出力内容の目次がハイパーリンク付きで出力されます。
基本統計量 - 目的変数
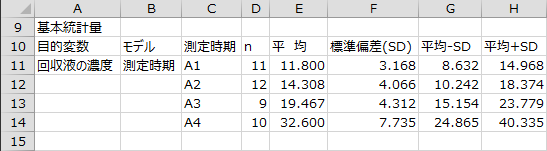
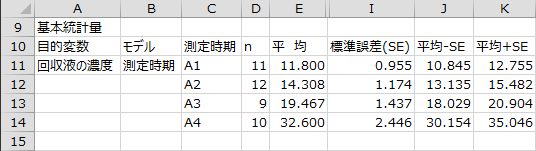
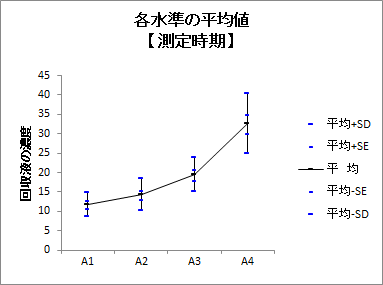
基本統計量として、目的変数のサンプルサイズ、平均、標準偏差（SD）、平均－SD、平均＋SD、標準誤差（SE）、平均?SE、平均＋SD、および、各水準の平均値のグラフが出力されます。
基本統計量 - 共変量
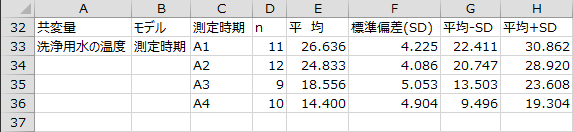
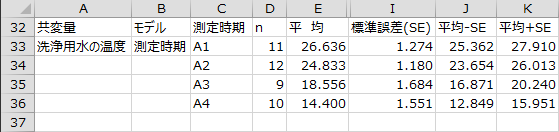
基本統計量として、共変量のサンプルサイズ、平均、標準偏差（SD）、平均－SD、平均＋SD、標準誤差（SE）、平均?SE、平均＋SD、および、各水準の平均値のグラフが出力されます。
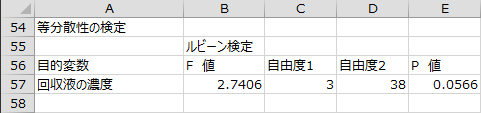
等分散性の検定
等分散性の検定として、ルビーン検定の結果が出力されます。
回帰の有意性の検定
回帰の有意性の検定の結果が出力されます。今回のように、共変量を含んだ交互作用項がある場合は、結果が出力されません。
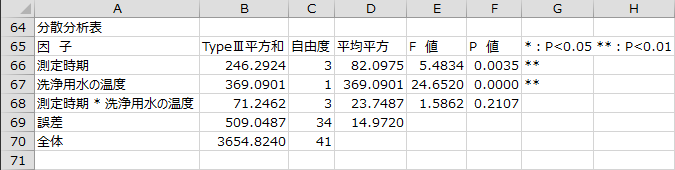
分散分析表
分散分析表として各因子の平方和、自由度、平均平方、F値、P値、判定結果が出力されます。「測定時期」と「洗浄用水の温度」の交互作用項を見てみると、P値が0.2107となり、5%有意水準では有意な結果ではありませんでした。したがって、測定時期ごとの回帰直線の傾きは平行であると仮定できます。
■ 回帰直線の有意性の検定と共分散分析
回帰直線の平行性を仮定できたので、続いて回帰直線の有意性の検定と共分散分析を行います。
ダイアログの設定
再度、下図のように表の先頭行「A3:C3」を選択します。メニューより［エクセル統計］→［分散分析・多重比較］→［共分散分析］を選択します。
［変数］タブ
ダイアログが表示される際、セル範囲「A3:C45」が［データ入力範囲］に自動で指定されます。「回収液の濃度」を［目的変数］に、「測定時期」を［固定因子］に、「洗浄用水の温度」を［共変量］にセットします。［OK］をクリックして分析を行います。
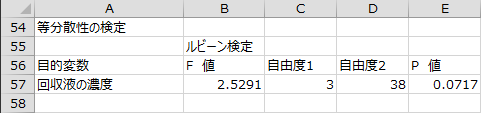
等分散性の検定
等分散性の検定として、ルビーン検定の結果が出力されます。
回帰の有意性の検定
回帰の有意性の検定の結果が出力されます。帰無仮説は「回帰式の傾きは0である」です。P値が0.01未満となったので、回帰式の傾きは0ではない、すなわち回帰式は有意であると考えられます。
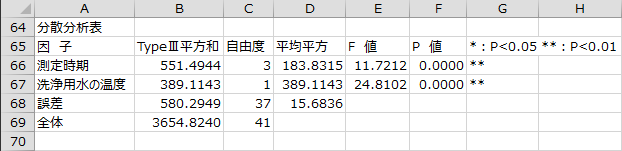
分散分析表
分散分析表として各因子の平方和、自由度、平均平方、F値、P値、判定結果が出力されます。「測定時期」はP値が0.01未満となり、有意水準5%で有意な結果となりました。
考察
洗浄用水の温度を考慮した上で、測定時期によって回収液の濃度が異なるか分析したところ、有意水準5%で回収液の濃度に差があるという結果になりました。
ダウンロード
この解析事例のExcel ファイルのダウンロードはこちらから → example_38.xlsx
このファイルは、エクセル統計の体験版に対応しています。
