マン=ホイットニーのU検定─エクセル統計による解析事例

2017/04/19

カテゴリ：解析事例

※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。

分析データ

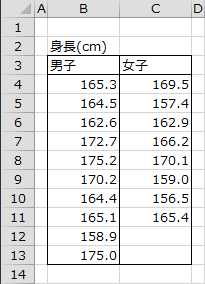
下図は、男子10人と女子10人の身長のデータです。エクセル統計を用いてマン=ホイットニーのU検定を行うことで、身長に関して男女間に差があるかどうか分析します。

ダイアログの設定

下図のように、セル「B3」を選択後、［Ctrl］キーを押しながらセル「C3」を選択します。メニューより［エクセル統計］→［ノンパラメトリック検定］→［マン=ホイットニーのU検定］を選択します。

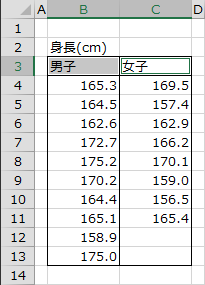
ダイアログが表示される際、セル範囲「B3:B13」が［標本1の範囲］に、セル範囲「C3:C13」が［標本2の範囲］に自動で指定されます。［OK］を選択して分析を実行します。

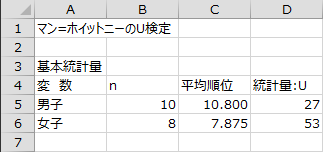
基本統計量

男子と女子のサンプルサイズ、平均順位、検定統計量：Uが出力されます。

平均順位の計算方法

男子と女子のデータをひとまとめにしたデータに順位を付け、各群の順位和を各群のサンプルサイズで割ることで平均順位が求められます。下図は男子と女子のデータをひとまとめにし、昇順で並べかえを行い、順序を付けたものです。（この表は出力されません。）

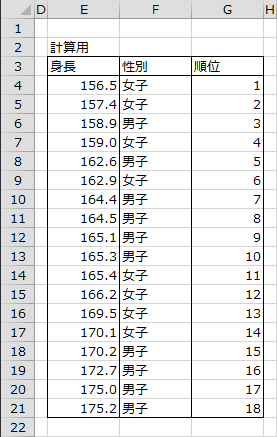
男子の順位和は、R₁=3+5+7+8+9+10+15+16+17+18=108 となります。サンプルサイズn₁=10で割ると、10.8 となります。

女子の順位和は、R₂=1+2+4+6+11+12+13+14=63 となります。サンプルサイズn₂=8で割ると、7.875 となります。

検定統計量の計算方法

検定統計量U_k は以下の式で求められます。

男子の検定統計量は、U₁=80+55-108=27 となります。

女子の検定統計量は、U₂=80+36-63=53 となります。

統計数値表による検定

マン=ホイットニーのU検定の統計量は、上で求めたU₁とU₂のうち小さい方の値となります。ここではU=27となり、両側検定を行った結果、帰無仮説「男女間の身長に差はない」は棄却されませんでした。（「－」は「5%有意」、「1%有意」いずれでもないことを示します）

正規化検定

検定統計量Uの平均と分散を用いて正規化検定を行った結果が出力されます。正規化検定においても帰無仮説は棄却されませんでした。

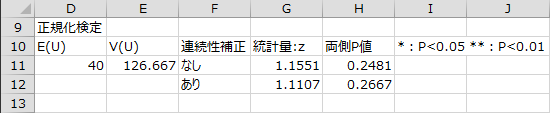
E(U)、V(U)、Zはそれぞれ以下の式で求められます。

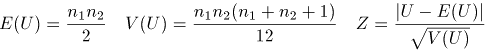
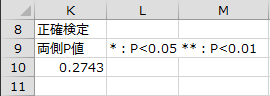
正確検定

並べ替えに計算よる正確検定を行った結果が出力されます。正確検定においても帰無仮説は棄却されませんでした。

考察

今回の男子と女子の身長のデータに関しては、男女間に差はないと言えます。

※ 掲載している画像は、エクセル統計による出力後に一部書式設定を行ったものです。

ダウンロード

この解析事例のExcel ファイルのダウンロードはこちらから　→　example_27.xlsx

このファイルは、エクセル統計の体験版に対応しています。

ブログ