共分散分析 : Analysis of Covariance (ANCOVA)
概要
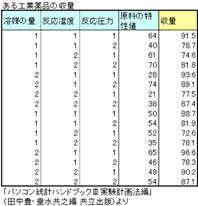
目的変数に与える因子の影響を分析するとき、因子のほかに定量的な変数の影響も考慮する場合に用いる手法です。このとき、目的変数に影響を与える定量的な変数のことを「共変量」といいます。データ例の場合、ある工業薬品の収量に影響を与える因子として、「溶媒の量」、「反応温度」、「反応圧力」があり、「原料の特性値」は共変量となります。
多重比較
各因子について以下の手法により共変量の影響を調整した多重比較を行うことが可能です。それぞれの手法の特徴については、「多重比較」をご覧ください。
| 全ての対比較を行う手法 | 対照群との対比較を行う手法 |
|---|---|
|
|
単純主効果の検定
分散分析で特定の2因子の交互作用が有意であった場合の下位検定として単純主効果の検定を行うことができます。単純主効果とは、ある2因子について、一方の因子の各水準における他方の因子の主効果のことです。さらに単純主効果の多重比較を行うことも可能で、フィッシャーのLSD、シェッフェ(Scheffe)、ボンフェローニ(Bonferroni)、テューキー(Tukey)の4手法を利用できます。
回帰の平行性
ある因子の水準間で共変量の回帰係数が共通であるかどうかを調べる場合、その因子と共変量との交互作用をモデルに含めて分析を行い、分散分析表でその交互作用のF検定の結果を参照してください。
回帰の有意性
共変量がモデルに複数含まれる場合、共変量全体として目的変数に寄与しているかどうかを検定し、「回帰の有意性の検定」として出力します。帰無仮説は「共変量は目的変数に寄与していない(回帰係数θ=0)」です。共変量それぞれについての有意性は、分散分析表で各共変量の主効果のF検定の結果を参照してください。共変量が1つの場合、「回帰の有意性の検定」の結果と分散分析表における共変量の主効果のF検定の結果は一致します。
分析例ファイルのダウンロード
共分散分析を使用する際のデータの形式やダイアログの指定方法、出力結果などを以下のExcelファイルからご確認いただけます。ダウンロードしてご参照ください。この分析例ファイルは、製品をご購入された場合にも自動でインストールされます。
なお、エクセル統計の無料体験版では、分析例ファイルのデータを実際に分析してみることができます。
処理対象データ
データベース形式
| データサイズ範囲 | 処理対象データ | 数値 | 文字列 | 空白 |
|---|---|---|---|---|
| 固定因子 | 1~7因子, 各因子2~250水準(Lk) | ○ | ○ | 欠 |
| 共変量 | 1~10変数 | ○ | 欠 | 欠 |
| 目的変数 | 1変数 | ○ | 欠 | 欠 |
※:○…処理可、×…処理不可、欠…欠損値として除く
データベース概要
- 3行以上のデータがあること
- 目的変数の分散が0ではないこと
- Π(Lk+1)≦5,000 を満たすこと
- nΠ(Lk+1)≦1,600万 を満たすこと
※ n…データ総数, Π…積記号, Lk…水準数
設定項目
Excelの[エクセル統計]タブから、[分散分析・多重比較]→[共分散分析]を選択すると以下のダイアログが表示されます。
「変数」タブ
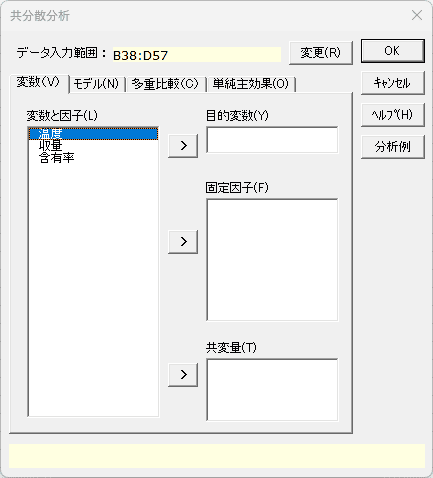
- データ入力範囲 必須
- データ入力範囲の変更を行う場合、[変更]ボタンを選択します。データ入力範囲のダイアログが表示されるので、データ入力範囲を設定して[戻る]ボタンを選択します。なお、データ入力範囲の先頭行は変数名となります。
- 目的変数 必須
- [変数と因子]から目的変数とする変数を設定します。
- 固定因子 必須
- [変数と因子]から固定因子とする因子を設定します。
- 共変量 必須
- [変数と因子]から共変量とする変数を設定します。
「モデル」タブ
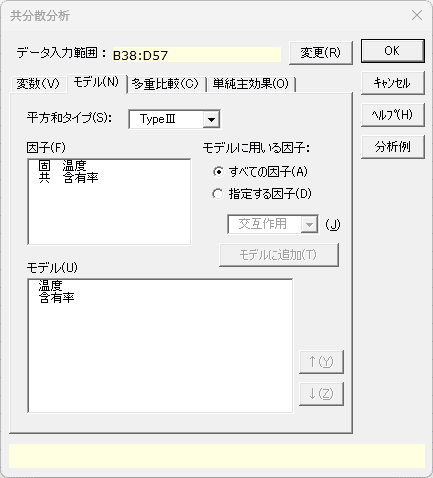
- 平方和タイプ
- 平方和タイプとして[TypeⅠ]、[TypeⅡ]、[TypeⅢ]のいずれかを選択します。初期設定は[TypeⅢ]となっています。
- モデルに用いる因子
- [すべての因子]と[指定する因子]のいずれかを選択します。初期設定は[すべての因子]となっています。
- すべての因子
- 固定因子のすべての組み合わせに共変量を加えたものがモデルとなります。
- 指定する因子
-
モデルに因子を追加する場合
- 「因子」で追加する因子を選択します。
- 選択した因子をモデルに追加する方法をプルダウンから選択します。
- [モデルに追加]ボタンをクリックします。
モデルから因子を削除する場合
- [モデル]で削除する因子を選択します。
- [モデルから削除]ボタンをクリックします。
なお、本製品では主効果をモデルから削除することはできません。
「多重比較」タブ
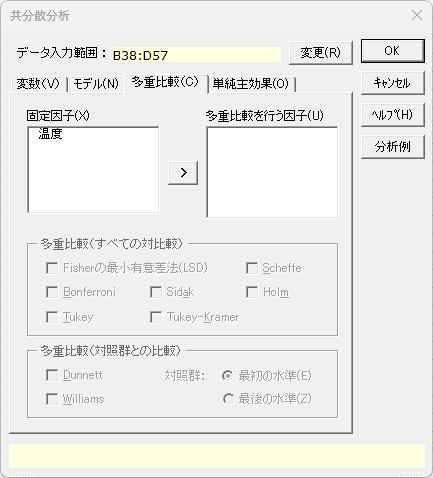
- 多重比較を行う因子を設定後、多重比較の方法を選択します。
「単純主効果」タブ
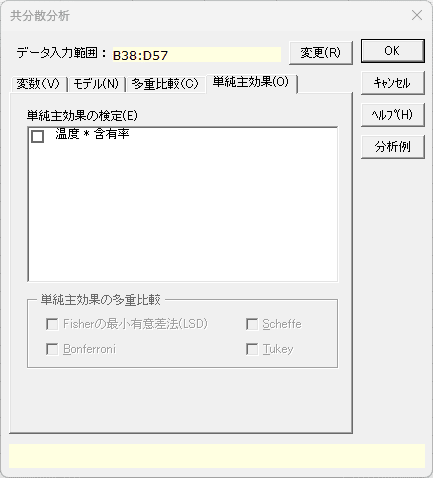
- 単純主効果の検定を行う交互作用を選択します。単純主効果についての多重比較も行う場合は実行する多重比較の方法を選択します。
出力内容
| 基本統計量 | 各水準の「サンプルサイズ」、「平均値」、「標準偏差(SD)」、「平均値-SD」、「平均値+SD」、「標準誤差(SE)」、「平均値-SE」、「平均値+SE」 |
|---|---|
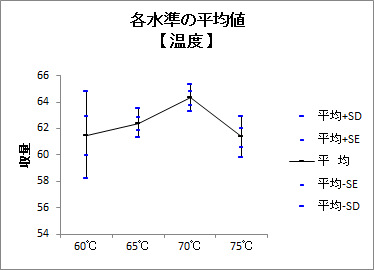
| 【グラフ】各水準の平均値 | 水準ごとに「平均値+SD」、「平均値+SE」、「平均値」、「平均値-SE」、「平均値-SD」を高低線で結んだグラフが出力されます。高低線の間で重なりが少ないほど水準間に差があることを示します。 |
| 等分散性の検定 | 帰無仮説:「被験者間因子の全ての水準で母分散は等しい」について「ルビーン検定」を行った結果 |
| 回帰の有意性の検定 | 帰無仮説:「共変量は目的変数に寄与していない」について、共変量全体としての目的変数への寄与の有無を検定した結果 |
| 分散分析表 | 全体の偏差平方和を、モデルタブにおいて指定したモデルの因子の平方和に分解した分散分析表が出力されます。 |
| 最小二乗平均 LSMEAN | 各主効果および交互作用の各水準の「最小二乗平均値」、「標準誤差」、「95%信頼区間」を出力。データの繰り返しに不揃いがある場合にそれを調整した標準誤差と95%信頼区間が出力されます。 |
| 多重比較検定 | ダイアログでチェックを入れた多重比較法によって、指定した被験者間因子の水準間の平均値差を検定した結果 |
| 各因子内の水準間の平均※1 | 2因子の組み合わせによる平均値とサンプルサイズが出力されます。 |
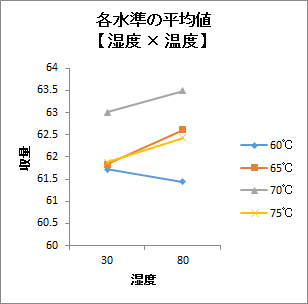
| 【グラフ】各水準の平均値※1 | 2因子の組み合わせによる各水準の平均値の折れ線グラフ |
| 単純主効果の検定※1 | 2因子の組み合わせによる単純主効果の検定の結果 |
| 多重比較検定※1 | 単純主効果における多重比較の結果 |
※1:[単純主効果の検定]にチェックを入れた場合にのみ出力されます。
出力内容とモデル
上記の各出力内容は、指定されたモデルによっては出力できない場合があります。こちらの表は本製品の対応状況となります。
| 基本統計量 | すべてのモデルで出力します。 |
|---|---|
| 各水準の平均値グラフ | すべてのモデルで出力します。 |
| 等分散性の検定 | すべての水準組み合わせでデータの繰り返しがない場合は出力できません。 |
| 回帰の有意性の検定 | すべてのモデルで出力します。 |
Type1またはType2平方和を指定した場合
| 分散分析表 | すべてのモデルで出力します。 |
|---|---|
| 多重比較 | データのない水準組み合わせがある場合は出力できません。 |
| 最小二乗平均 LSMEAN | データのない水準組み合わせがある場合は出力できません。 |
| 単純主効果の検定 | データのない水準組み合わせがある場合は出力できません。 |
Type3平方和を指定した場合
|
|
|---|
参考文献
- Lynne Edwards, "Applied Analysis of Variance in Behavioral Science", Chapman and Hall/CRC, 1993.
- Michihiro Yoshida, "Exact probabilities associated with Tukey's and Dunnett's multiple comparisons procedures in imbalanced one-way ANOVA", Journal of the Japanese Society of Computational Statistics 1, pp.111-122, 1988.
- Ramon C. Littell, Rudolf J. Freund, Philip C. Spector, "SAS System for Linear Models, Third Edition", SAS Institute, 1991.
- Shayle R. Searle, "Linear Models for Unbalanced Data", Wiley-Interscience, 2006.
- アラン・グラフェン, ロージー・ヘイルズ, "一般線形モデルによる生物科学のための現代統計学―あなたの実験をどのように解析するか", 共立出版, 2007.
- 安藤 貞一, 朝尾 正, "実験計画法演習", 日本科学技術連盟, 1968.
- 石村 貞夫, "分散分析のはなし", 東京図書, 1992.
- オリヴィエ・ダン, V.A.クラーク, "応用統計学―分散分析と回帰分析", 森北出版, 1975.
- 高橋 行雄, 芳賀 敏郎, 大橋 靖雄, "SASによる実験データの解析", 東京大学出版会, 1989.
- 田中 豊, "パソコン実験計画法入門", 現代数学社, 1985.
- 田中 豊, 垂水 共之, "パソコン統計解析ハンドブック 3 実験計画法編", 共立出版, 1986.
- 田中 豊, 脇本 和昌, 垂水 共之, "パソコン統計解析ハンドブック 5 多変量分散分析・線形モデル編", 共立出版, 1989.
- 永田 靖, 吉田 道弘, "統計的多重比較法の基礎", サイエンティスト社, 1997.
- 広津 千尋, "実験データの解析―分散分析を超えて", 共立出版, 1992.
- 広津 千尋, "分散分析", 教育出版, 1976.
- 森 敏昭, 吉田 寿夫, "心理学のためのデータ解析テクニカルブック", 北大路書房, 1990.
- 山内 光哉, "心理・教育のための分散分析と多重比較―エクセル・SPSS解説付き", サイエンス社, 2008.
- "SAS/STATTM ユーザーズガイド Release 6.03 Edition", SAS出版局, 1992.


