クロス集計表の作成と分析─エクセル統計による解析事例
2017/04/19
カテゴリ：解析事例
タグ：アンケート
※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。
分析データ
下図のデータは、女性の肺癌患者108名、対照群108名を選出し、喫煙歴について調査した結果です。
分析の目的
肺癌の有無と喫煙歴の有無との関係を調べます。
データラベルの選択
セル「C3」を選択後、［Ctrl］キーを押しながらセル「D3」を選択します。
メニューの選択
メニューより［エクセル統計］→［集計表の作成と分析］→［クロス集計表の作成と分析］を選択します。「肺癌」が［表頭］に、「喫煙歴」が［表側］に設定された状態でダイアログが表示されます。
［表頭］タブ
表頭の「尺度水準」として［名義］を選択します。「カテゴリーの順序」として［出現順］を選択します。
［表側］タブ
表側の「尺度水準」として［名義］を選択します。「カテゴリーの順序」として［出現順］を選択します。
［レイアウト］タブ
「合計の位置」として［右端・下側］を選択します。「各セルの値」として［度数］を選択します。［次へ］ボタンをクリックします。
［全般］タブ
「カイ二乗検定」や「名義」に関する統計量について、出力するものにチェックを入れます。
［2×2］タブ
2行×2列のクロス集計表から算出可能な統計量について、出力するものにチェックを入れます。［OK］ボタンをクリックして分析を実行します。
クロス集計表
「肺癌」を表頭、「喫煙歴」を表側とするクロス集計表が出力されます。
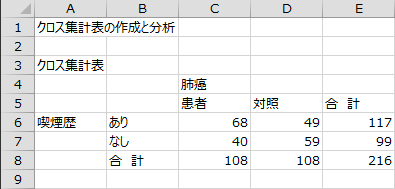
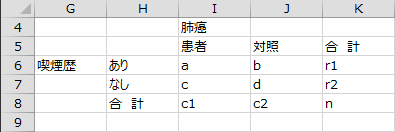
文字列表
クロス集計表が2行×2列の場合、各セルを示す文字列を定義した表が出力されます。
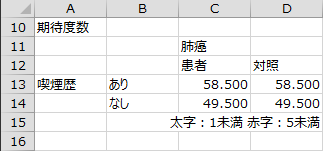
期待度数
各セルの期待度数が出力されます。期待度数は、行要素の合計と列要素の合計の比率から逆算して期待される度数です。
カイ二乗検定
カイ二乗検定の結果が出力されます。帰無仮説は「行と列は独立である」です。
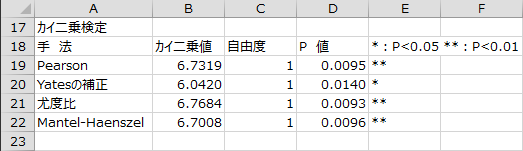
- Pearson：
- Pearsonのカイ二乗統計量は、観測度数と期待度数の差異から計算します。独立性の検定として用いられる最も一般的な統計量です。対立仮説は「行と列の間に一般連関がある」です。
- Yatesの補正：
- Pearsonのカイ二乗統計量にカイ二乗分布の連続性に対する調整を施した値です。対立仮説は「行と列の間に一般連関がある」です。
- 尤度比：
- 尤度比カイ二乗統計量は、観測度数と期待度数の比率から計算します。対立仮説は「行と列の間に一般連関がある」です。
- Mantel-Haenszel：
- Mantel-Haenszelのカイ二乗統計量は、行変数と列変数の相関係数から計算します。対立仮説は「行と列の間に線形連関がある」です。
名義
表頭と表側がともに名義尺度の場合に得られる統計量が出力されます。いずれも行と列の関連の強さを表す指標で、0以上1以下の値をとります。
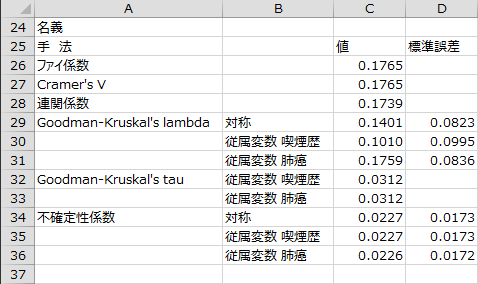
- ファイ係数：
- Pearsonのカイ二乗統計量から計算します。2行×2列の場合はCramer's Vに等しくなります。
- Cramer's V：
- Pearsonのカイ二乗統計量から計算します。2行×2列の場合はファイ係数に等しくなります。
- 連関係数：
- Pearsonのカイ二乗統計量から計算します。
- Goodman-Kruskal's lambda（対称）：
- 下の2つの非対称ラムダの平均値です。方向性のないラムダ。
- Goodman-Kruskal's lambda（従属変数 喫煙歴）：
- 列変数（肺癌）を利用することによって行変数（喫煙歴）の予測がどの程度改善するかを求めた値です。
- Goodman-Kruskal's lambda（従属変数 肺癌）：
- 行変数（喫煙歴）を利用することによって列変数（肺癌）の予測がどの程度改善するかを求めた値です。
- Goodman-Kruskal's tau（従属変数 喫煙歴）：
- 列変数（肺癌）を利用することによって行変数（喫煙歴）の予測がどの程度改善するかを求めた値です。ラムダとは計算方法が異なります。
- Goodman-Kruskal's tau（従属変数 肺癌）：
- 行変数（喫煙歴）を利用することによって列変数（肺癌）の予測がどの程度改善するかを求めた値です。ラムダとは計算方法が異なります。
- 不確定性係数（対称）：
- 下の2つの非対称不確定性係数の対称版。
- 不確定性係数（従属変数 喫煙歴）：
- 列変数（肺癌）を利用することによる行変数（喫煙歴）の不確定性（エントロピー）の減少率。
- 不確定性係数（従属変数 肺癌）：
- 行変数（喫煙歴）を利用することによる列変数（肺癌）の不確定性（エントロピー）の減少率。
2行×2列のクロス集計表から得られる統計量
2行×2列のクロス集計表から得られる統計量が出力されます。計算方法の文字列は、上述した文字列表に対応しています。
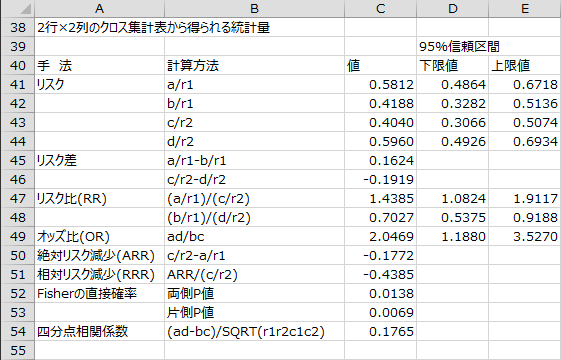
- リスク差：
- 「喫煙歴ありに占める肺癌患者の割合」から「喫煙歴ありに占める対照者の割合」を引いた値です。
- 「喫煙歴なしに占める肺癌患者の割合」から「喫煙歴なしに占める対照者の割合」を引いた値です。
- リスク比：
- 「喫煙歴なしの肺癌患者」に対する「喫煙歴ありの肺癌患者」の比です。
- 「喫煙歴なしの対照者」に対する「喫煙歴ありの対照者」の比です。
- オッズ比：
- 「喫煙歴なしにおける肺癌患者のオッズ」に対する「喫煙歴ありにおける肺癌患者のオッズ」の比です。
- 絶対リスク減少：
- 「喫煙歴なしに占める肺癌患者の割合」から「喫煙歴ありに占める肺癌患者の割合」を引いた値です。
- 相対リスク減少：
- 絶対リスク減少を「喫煙歴なしに占める肺癌患者の割合」で割り相対値としたものです。
- Fisherの直接確率：
- カイ二乗検定のような近似値ではなく、超幾何分布を用いてP値を直接求めた結果です。
- 四分点相関係数：
- ピアソンの積率相関係数を2行×2列のクロス集計表に適用したものです。2行×2列のクロス集計表では、ファイ係数とCramer's Vに等しくなります。
考察
カイ二乗検定の結果は近似値なのでFisherの直接確率を見ると、両側P値は0.0138であり、有意水準5%で肺癌と喫煙歴には関連があると言えます。
名義尺度間の関連の程度を表す指標を見ると、0.2を上回るものはなく、関連の程度は低めです。
オッズ比が2.0469なので、喫煙歴ありの人は喫煙歴なしの人に比べて肺癌であるリスクが約2倍であると言えます。
※ 掲載している画像は、エクセル統計による出力後に一部書式設定を行ったものです。
ダウンロード
この解析事例のExcel ファイルのダウンロードはこちらから → example_15.xlsx
このファイルは、エクセル統計の体験版に対応しています。
