統計検定2級CBT公式問題集の解説（データ収集の分野・確率の分野）

2023/07/21

カテゴリ：統計検定

※統計検定2級解説記事一覧はこちら※

下記のリンクからそれぞれの問題の解説に飛ぶことができます。

■データ収集の分野

問1：各標本抽出の性質に関する問題
問2：研究の形態に関する問題
問3：フィッシャーの3原則に関する問題
問4：非標本誤差に関する問題

■確率の分野

問1：積事象の確率に関する問題
問2：ベイズの定理に関する問題
問3：条件付き期待値に関する問題
問4：事象間の排反・独立に関する問題
問5：2段階実験確率変数の期待値に関する問題
問6：対戦順の説明の正誤に関する問題

問1（データ収集の分野）

I：
「当日のすべての搭乗客（＝母集団）」の中からランダムに調査対象者を選ぶ方法です。このような方法を「単純無作為抽出法」といいます。

II：
午前出発便と午後出発便という2つのグループそれぞれからランダムに調査対象者を選ぶ方法です。このような方法を「層化抽出法（層別抽出法）」といいます。

III：
小集団（この場合は、1台の飛行機における搭乗客）の中からいくつかの小集団を無作為抽出し、それぞれの小集団において全数調査を行う方法です。このような方法を「集落抽出法（クラスター抽出法）」といいます。

その他の標本の抽出方法については「16-3. 標本の抽出方法」をご覧ください。

問2（データ収集の分野）

実験研究とは、研究対象に対して何らかの介入（投薬や治療など）を行い、その効果を検証するための研究デザインのことです。一方、観察研究とは、研究対象に対して介入（投薬や治療など）を行わなずに、観察によってデータを集めて解析を行う研究デザインのことです。

A：
特に介入は行っていないので、この研究は「観察研究」です。

B：
新しい治療法、もしくは従来からの治療法を適用しており、これらは介入になります。したがって、この研究は「実験研究」です。

C：
特に介入は行っていないので、この研究は「観察研究」です。

研究デザインの詳細については「16-4. 研究デザイン」をご覧ください。

問3（データ収集の分野）

I：○
「無作為化」とは、実験の順序や場所などが複数ある場合に、比較したい処理群を無作為に割り付けることです。目的とする要因以外に結果に影響を与える要因がある場合に、無作為化によってその影響の偏りをできるだけ小さくすることができます。すなわち、系統誤差を偶然誤差に取り込むことができます。

II：×
「繰り返し」とは、複数の処理を比較する際にそれぞれの処理に対して2回以上の繰り返し実験（評価）を行うことです。同じ処理条件であれば、同一の被験者から繰り返しデータを取得しても複数の被験者からデータを取得しても、どちらも「繰り返し」になります。

III：×
「局所管理」とは、実験を行う時間や場所を区切ってブロックを作り、そのブロック内でのバックグラウンドができるだけ均一になるように管理することです。実験を監督・監視する人を各ブロックに無作為に割り付けるという意味ではありません。

フィッシャーの3原則の詳細については「31-1. フィッシャーの3原則」をご覧ください。

問4（データ収集の分野）

標本誤差とは、「母集団から抽出した標本を用いて、母集団における平均や比率などの数値を推定した場合に、母集団の統計量と標本から算出した推定値との差」のことです。標本調査をする限り、この標本誤差を0にすることはできません。与えられた例の中で標本誤差に該当するものは①になります。

一方の非標本誤差は、標本誤差以外の誤差のことで、標本自体の性質とは関係無い要因によって生じます。例えば、標本やデータの選び方、調査方法の欠陥、データの欠損（無回答）、データの測定の誤差などが非標本誤差に含まれます。

問1（確率の分野）

問題文で与えられた情報を元に確率を整理してみます。検定試験に合格する事象を $A$ 、検定試験の対策講座を受講する事象を $B$ とします。

対策講座を受講する確率 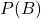$P(B)$ ：0.2
対策講座を受講しない確率 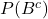$P(B^c)$ ：1-0.2=0.8
対策講座を受講して合格する確率 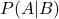$P(A | B)$ ：0.7
対策講座を受講して不合格となる確率 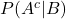$P(A^c | B)$ ：1-0.7=0.3
対策講座を受講せず合格する確率 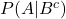$P(A | B^c)$ ：0.3
対策講座を受講せず不合格となる確率 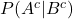$P(A^c | B^c)$ ：1-0.3=0.7

ある事象Bが起こるという条件のもとで事象 $A$ が起こる場合、この条件付き確率は $P(A|B)$ と表され、次の式により計算できます。

$P(A|B) = \displaystyle \frac{P(A \cap B)}{P(B)}$

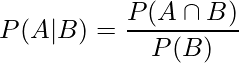
今知りたいのは、無作為に選んだ1人が検定試験の対策講座を受講し、かつ、検定試験に合格する確率なので $P(A \cap B)$ になります。したがって、

$0.7 = \displaystyle \frac{P(A \cap B)}{0.2}$

$P(A \cap B) = 0.2 \times 0.7 = 0.14$

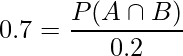
となります。

条件付き確率については「10-1. 条件付き確率とは」をご覧ください。

問2（確率の分野）

問題文で与えられた情報を元に確率を整理してみます。クッキーの箱にカモノハシの絵がプリントされている事象を $A$ 、クッキーの箱が工場A、Bで製造される事象をそれぞれ $B_a$ 、 $B_b$ とします。

クッキーの箱が工場Aで製造される確率 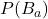$P(B_a)$ ：0.7
クッキーの箱が工場Bで製造される確率 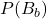$P(B_b)$ ：0.3
工場Aで製造されたクッキーの箱にカモノハシの絵がプリントされている確率 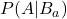$P(A | B_a)$ ：0.02
工場Bで製造されたクッキーの箱にカモノハシの絵がプリントされている確率 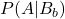$P(A | B_b)$ ：0.08

事象 $A$ が起こるという条件のもとで、 $k$ 種類の事象 $B \hspace{3mm}$ （ $B_1, B_2, \cdots , B_k$ ：ただしこれらは互いに排反とする）が起こるとします。このとき、事象 $A$ が起こるという条件のもとで事象 $B_i$ が起こる条件付き確率 $P(B_i|A)$ は、ベイズの定理を用いて次の式から求められます。

$\displaystyle P(B_i|A) =\frac{P(B_i)P(A|B_i)}{\sum_{j=1}^{k} P(B_{j})P(A|B_{j})}$

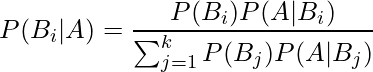
今知りたいのは、無作為に選んだクッキーの箱1個にカモノハシの絵がプリントされていたときに、そのクッキーの箱が工場Aで製造された確率なので $P(B_a|A)$ になります。したがって、

$\displaystyle P(B_a|A) =\frac{P(B_a)P(A|B_a)}{P(B_{a})P(A|B_{a}) + P(B_{b})P(A|B_{b})}$

$\displaystyle P(B_a|A) =\frac{0.7 \times 0.02}{0.7 \times 0.02 + 0.3 \times 0.08} = \frac{0.014}{0.014 + 0.024} = 0.368$

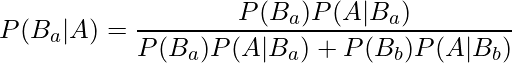
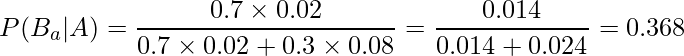
となります。

条件付き確率については「10-4. ベイズの定理」をご覧ください。

問3（確率の分野）

何回か試行を行う場合に成功するまでの試行回数に関する問題なので、幾何分布を使います。幾何分布とは、成功確率が $p$ である独立なベルヌーイ試行を繰り返す時、初めて成功するまでの試行回数 $X$ が従う確率分布のことです。確率変数 $X$ が幾何分布に従う場合、成功確率が $p$ の試行において、 $k$ 回目で初めて成功する確率（ $X=k$ となる確率）は次の式から計算できます。

$\begin{eqnarray*} P(X=k)=(1-p)^{k-1} p & (k=1,2,3,\cdots) \\ \end{eqnarray*}$

また、期待値は

$\displaystyle E(X) = \frac{1}{p}$

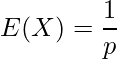
となります。これまで5回くじを引いて全て外れだったとしても、その結果は6回目以降には影響を与えません（各試行は独立なベルヌーイ試行のため）。したがって、5回のくじが終わった時点からあたりが出るまでにくじを引く回数の期待値は、

$\displaystyle E(X) = \frac{1}{\frac{1}{10}} = 10$

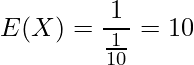
となります。

幾何分布については「13-5. 幾何分布」をご覧ください。

問4（確率の分野）

まずはじめに「独立」と「排反」の意味について確認します。

独立：2つの事象があるとき、それぞれの事象の結果が互いに影響しあうことがないとき、2つの事象は「独立である」と言います。
排反：複数の事象があるとき、それぞれの事象が同時に起こらないことです。

2つの事象が独立である場合、2つの積事象の確率は事象同士の確率の積で算出することができます。つまり、独立な事象 $A$ 、事象 $B$ を同時に満たす事象（＝積事象 $A \cap B$ ）の確率について次のような関係が成り立ちます。

$P(A \cap B) =P(A) \times P(B)$

この問題では、

$\begin{eqnarray*} \displaystyle P(A \cap B) &=& P(A) + P(B) - P(A \cup B) \\ &=& 0.4 + 0.35 - 0.61 \\ &=& 0.14 \\ &=& P(A) \times P(B) \end{eqnarray*}$

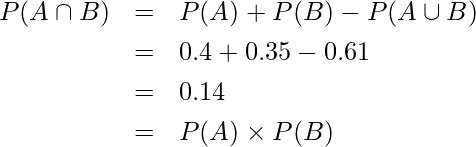
となることから、事象 $A$ と事象 $B$ は独立であるといえます。一方、

$\displaystyle P(A \cap B) = 0.14 \neq 0$

であることから、事象 $A$ と事象 $B$ は同時に起こりうる、すなわち排反ではないといえます。

問5（確率の分野）

袋Aには赤玉が2個、袋Bには赤玉が1個入っているので、袋Aもしくは袋Bから玉を2個取り出すとき、赤玉が取り出されうる回数は「0回、1回、2回」のいずれかになります。まず、それぞれの確率を計算します

＜赤玉が0回取り出される場合＞

サイコロが2以下の目→袋Aから白玉が2回取り出される

$\displaystyle P[X=0] = \frac{2}{6} \times \left( \frac{3}{5} \times \frac{3}{5} \right) = \frac{9}{75}$

サイコロが3以上の目→袋Bから白玉が2回取り出される

$\displaystyle P[X=0] = \frac{4}{6} \times \left( \frac{4}{5} \times \frac{4}{5} \right) = \frac{32}{75}$

＜赤玉が1回取り出される場合＞

サイコロが2以下の目→袋Aから白玉が1回、赤玉が1回取り出される

$\displaystyle P[X=1] = \frac{2}{6} \times \left( 2 \times \frac{3}{5} \times \frac{2}{5} \right) = \frac{12}{75}$

サイコロが3以上の目→白玉が1回、赤玉が1回取り出される

$\displaystyle P[X=1] = \frac{4}{6} \times \left( 2 \times \frac{4}{5} \times \frac{1}{5} \right) = \frac{16}{75}$

＜赤玉が2個回取り出される場合＞

サイコロが2以下の目→袋Aから赤玉が2回取り出される

$\displaystyle P[X=2] = \frac{2}{6} \times \left( \frac{2}{5} \times \frac{2}{5} \right) = \frac{4}{75}$

サイコロが3以上の目→赤玉が2回取り出される

$\displaystyle P[X=2] = \frac{4}{6} \times \left( \frac{1}{5} \times \frac{1}{5} \right) = \frac{2}{75}$

赤玉が0個取り出される確率は $\displaystyle \frac{9}{75} + \frac{32}{75} = \frac{41}{75}$ 、1個取り出される確率は $\displaystyle \frac{12}{75} + \frac{16}{75} = \frac{28}{75}$ 、2個取り出される確率は $\displaystyle \frac{4}{75} + \frac{2}{75} = \frac{6}{75}$ なので、赤玉が取り出される回数の期待値は