2021年6月統計検定2級の問題の解説(その1)
2021/07/31
カテゴリ:統計検定
タグ:2021年6月
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
- 問1:データの分布と歪度に関する問題
- 問2:幾何平均に関する問題
- 問3:パーシェ指数の算出に関する問題
- 問4:増加率/減少率に関する問題
- 問5:相関係数に関する問題
- 問6:相関係数の算出に関する問題
- 問7:標本抽出に関する問題
問1 [1]
ガタガタしていて少しわかりにくい分布ですが、ピークが左側にあることが分かります。このような分布は「右裾が長い」もしくは「右に歪んだ」もしくは「左に偏った」分布とよばれます。右裾が長い分布の場合、歪度は正の値を取ります。
歪度の計算の詳細についてはこちらをご覧ください。
問2 [2]
1950年から1951年における変化率は、![]() となります。
となります。
同様にして、1951年から1952年における変化率は![]() 、1952年から1953年における変化率は
、1952年から1953年における変化率は![]() 、1953年から1954年における変化率は
、1953年から1954年における変化率は![]() となります。
となります。
これら4つの値の幾何平均が1950年から1954年の年次変化率となります。したがって、
から、15.4%となります。一般的な電卓を使って計算する場合には、ルートの計算を2回繰り返します。
問3 [3]
パーシェ指数を実際に算出する問題です。公式を覚えていないと絶対に解けない問題です。今までは計算式を選ばせる問題が多かったような気がしますが。
パーシェ指数は「比較年の価格と比較年の購入数量をかけたものの和」を「基準年の価格と比較年の購入数量を書けたものの和」で割ることで算出できます。したがって、
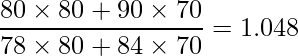
となります。パーシェ指数を含む様々な物価指数の詳細についてはこちらをご覧ください。
問4 [4]
1990年における東京都の新聞発行部数を100とすると、2019年は57であることがグラフから読み取れます。つまり、1990年の発行部数における「43/100」が減少してしまった発行部数となります。
したがって、減少した発行部数は
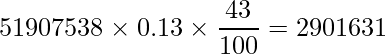
と計算できます。
問4 [5]
問題文で与えられた式から、出てくる値はだいたい±数%くらいであることが予想できます。このような問題では、適当な値を入れてみてどういう値が出そうかをまずは把握しておくのがポイントです。すると、縦軸の値から③と⑤は選択肢からはじくことができます。
次に、元のグラフをよく見てみます。元のグラフから分かることは、「2005年以降はどちらの都県も発行部数が単純減少である」ということです。つまり、2005年以降は前年比増加率のグラフは0%を超えないということです。
この条件を満たすグラフは①のみなので、①が正しい答えとなります。
問5 [6]
I:○ 飛距離点はだいたい20~80の範囲の値を、飛型点はだいたい46~56の範囲の値をとります。飛距離点のほうがばらつきの大きな値を取ることから、分散も大きくなります。
II:○ 2つの散布図から飛距離点と飛型点の直線的な相関関係(左側の図)のほうが強いことが分かります。
III:○ 飛距離点と飛型点の散布図に回帰直線を当てはめると(実際に線を引いてみて、ずずずっとy軸まで線を伸ばしてみると)、切片は42くらいになることが予想されます。
問5 [7]
飛距離が![]() mのとき、飛距離点は
mのとき、飛距離点は![]() であることから、
であることから、![]() に直接かかっている係数「2」についてのみ考えればOKです。というのも、同じ値を一律足したり引いたりしても、共分散・相関係数は変化しないためです。つまりこの問題をとてもシンプルに言い換えると、「
に直接かかっている係数「2」についてのみ考えればOKです。というのも、同じ値を一律足したり引いたりしても、共分散・相関係数は変化しないためです。つまりこの問題をとてもシンプルに言い換えると、「![]() と
と![]() の共分散・相関係数は
の共分散・相関係数は![]() と
と![]() の共分散・相関係数の何倍か」ということになります。
の共分散・相関係数の何倍か」ということになります。
共分散は次の式から算出できます(詳細はこちらをご覧ください)。![]() が2倍になると共分散は2倍になりますし、
が2倍になると共分散は2倍になりますし、![]() が1/2になると共分散は1/2になります。
が1/2になると共分散は1/2になります。
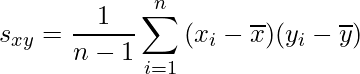
相関係数は次の式から算出できます(詳細はこちらをご覧ください)。![]() が2倍になっても1/2になっても相関係数は変わりません。
が2倍になっても1/2になっても相関係数は変わりません。
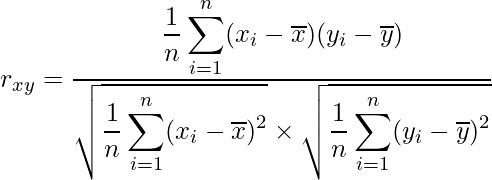
問6 [8]
[7]で示した式を使って相関係数を求めるためにまず、共分散(分子)を計算します。共分散を求めるにはこちらの![]() の式を使います。
の式を使います。
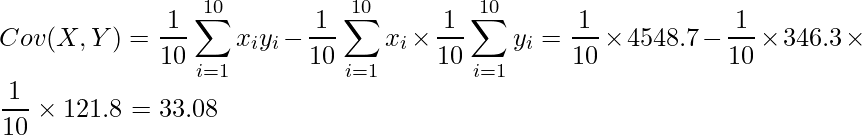
次に標準偏差(分母)を計算します。不偏分散の値が与えられているので、この値を使って、
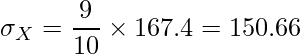
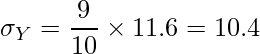
と計算できます。したがって、相関係数は次のように計算できます。
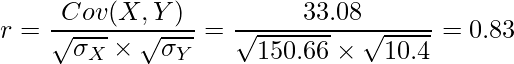
問7 [9]
部長の抽出にあたっては「事業部ごとに、いくつかの部を無作為に抽出」とあることから、事業部という「層」を使って「層」ごとに抽出を行っていることが分かります。したがって、この抽出方法は「層化抽出法」です。
次に、社員の抽出にあたっては、層化抽出された部の社員の中からさらに無作為抽出を行っていることから、この抽出方法は「層化二段抽出法」となります。








