統計検定2級CBT公式問題集の解説(推定の分野)
2023/11/01
カテゴリ:統計検定
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
- 問1:推定値と標準誤差に関する問題
- 問2:
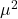 の不偏推定量に関する問題
の不偏推定量に関する問題 - 問3:
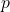 が未知の標本サイズに関する問題
が未知の標本サイズに関する問題 - 問4:捕獲再捕獲法信頼区間に関する問題
- 問5:非正規母集団に対する母平均の信頼区間に関する問題
- 問6:母比率の差の信頼区間と検定に関する問題
問1
北海道と沖縄県の全体(15歳以上の全人口)は
です。また、北海道と沖縄の野球の行動者数は
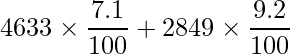
です。したがって、北海道と沖縄県の全体における野球の行動者の母比率の推定値 ![]() は
は
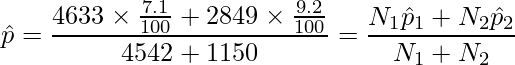
となります。![]() と
と ![]() は独立なので、
は独立なので、![]() の分散は
の分散は
![Rendered by QuickLaTeX.com \displaystyle V[\hat{p}] = \left(\frac{N_1}{N_1 + N_2}\right)^2V[\hat{p}_1] + \left(\frac{N_2}{N_1 + N_2}\right)^2V[\hat{p}_2]](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-4883752e583cc8e62728e3e141a99dc9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle V[\hat{p}] = \left(\frac{N_1}{N_1 + N_2}\right)^2\frac{\hat{p}_1(1-\hat{p}_1)}{n_1} + \left(\frac{N_2}{N_1 + N_2}\right)^2\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-9504e765f16f7458231ed2c6c423dd96_l3.png)
となるので、標準誤差は
![Rendered by QuickLaTeX.com \displaystyle SE = \sqrt{V[\hat{p}]} = \sqrt{\left(\frac{N_1}{N_1 + N_2}\right)^2\frac{\hat{p}_1(1-\hat{p}_1)}{n_1} + \left(\frac{N_2}{N_1 + N_2}\right)^2\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-666c6eb97909e85b8b5a9eeef062d65f_l3.png)
となります。
標本比率を用いた母比率の信頼区間算出の詳細については「21-1. 母比率の信頼区間の求め方1」をご覧ください。
問2
![]() の不偏推定量
の不偏推定量 ![]() は
は
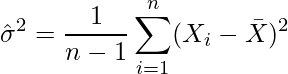
です。![]() を展開すると
を展開すると
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[\hat{\sigma}^2] &=& E\left[\frac{1}{n-1}\sum_{i=1}^{n} (X_i - \bar{X})^2 \right] \\ &=& E\left[\frac{1}{n-1}\sum_{i=1}^{n} (X_i - \mu + \mu - \bar{X})^2 \right] \\ &=& E\left[\frac{1}{n-1}\sum_{i=1}^{n} ((X_i - \mu) + (\mu - \bar{X}))^2 \right] \\ &=& E\left[\frac{1}{n-1}\sum_{i=1}^{n} ((X_i - \mu)^2 + 2(X_i - \mu)(\mu - \bar{X}) + (\mu - \bar{X})^2) \right] \\ &=& E\left[\frac{1}{n-1} \left(\sum_{i=1}^{n} (X_i - \mu)^2 + \sum_{i=1}^{n}2(X_i - \mu)(\mu - \bar{X}) + \sum_{i=1}^{n}(\mu - \bar{X})^2) \right] \\ &=& E\left[\frac{1}{n-1} \left(\sum_{i=1}^{n} (X_i - \mu)^2 + 2(\mu - \bar{X})\sum_{i=1}^{n}(X_i - \mu) + \sum_{i=1}^{n}(\mu - \bar{X})^2) \right] \\ &=& E\left[\frac{1}{n-1} \left(\sum_{i=1}^{n} (X_i - \mu)^2 + 2(\mu - \bar{X})n(\bar{X} - \mu) + n(\mu - \bar{X})^2) \right] \\ &=& E\left[\frac{1}{n-1} \left(\sum_{i=1}^{n} (X_i - \mu)^2 - 2n(\mu - \bar{X})^2 + n(\mu - \bar{X})^2) \right] \\ &=& E\left[\frac{1}{n-1} \left(\sum_{i=1}^{n} (X_i - \mu)^2 - n(\mu - \bar{X})^2 \right) \right] \\ &=& \frac{1}{n-1}E\left[\sum_{i=1}^{n} (X_i - \mu)^2 - n(\bar{X} - \mu)^2 \right] \\ &=& \frac{1}{n-1} \left(E\left[ \sum_{i=1}^{n} (X_i - \mu)^2 \right] - E\left[n(\bar{X} - \mu)^2 \right] \right) \\ &=& \frac{1}{n-1} \left(E\left[ \sum_{i=1}^{n} (X_i - \mu)^2 \right] - nE\left[ \left( \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu) \right)^2 \right] \right) \\ &=& \frac{1}{n-1} \left( n\sigma^2 - n\left( n \times \left(\frac{\sigma}{n} \right)^2 \right) \right) \\ &=& \frac{1}{n-1} \left( n\sigma^2 - \sigma^2 \right) \\ &=& \frac{1}{n-1} (n-1)\sigma^2 \\ &=& \sigma^2 \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-28106ab7bc42506291146b44ed57eec2_l3.png)
となることからも確認できます。一方、![]() の分散は期待値を用いて次の式から求められます。
の分散は期待値を用いて次の式から求められます。
この式を変形すると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle V[X] &=& E[X^2] - \mu^2 \\ \mu^2 &=& E[X^2] - V[X] \\ \mu^2 &=& {\bar{X}}^2 - \frac{\sigma^2}{n} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-59fb35447f1d96f11e0ff29e128037ce_l3.png)
となります。
不偏分散の詳細については「数学ノート 標本分散の一致性と不偏性」をご覧ください。
問3
サンプルサイズを ![]() 、標本比率を
、標本比率を ![]() とすると、次の式から母比率
とすると、次の式から母比率 ![]() の95%信頼区間を求めることができます。
の95%信頼区間を求めることができます。
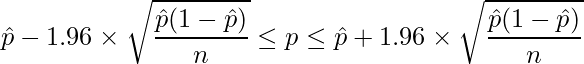
この式から、信頼区間の幅は
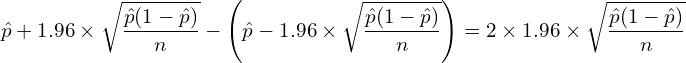
となります。問題文より
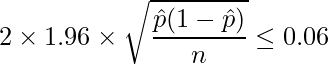
となる最小の ![]() を求めれば良いことがわかります。
を求めれば良いことがわかります。![]() について事前の情報が全くない場合には、
について事前の情報が全くない場合には、![]() を用いることで
を用いることで ![]() が最大となるので、上の式を用いて「最もサンプルサイズが必要な場合の最小のサンプルサイズ」を計算できます。したがって、
が最大となるので、上の式を用いて「最もサンプルサイズが必要な場合の最小のサンプルサイズ」を計算できます。したがって、
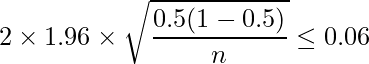
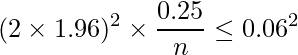
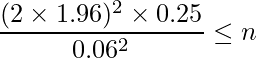
となります。
母比率の計算方法については「21-1. 母比率の信頼区間の求め方1」をご覧ください。
問4
サンプルサイズを ![]() 、標本比率を
、標本比率を ![]() とすると、次の式から母比率
とすると、次の式から母比率 ![]() の95%信頼区間を求めることができます。
の95%信頼区間を求めることができます。
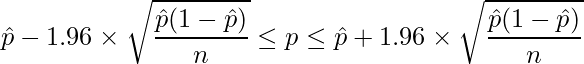
問題文より、![]() 、
、![]() であることから、
であることから、
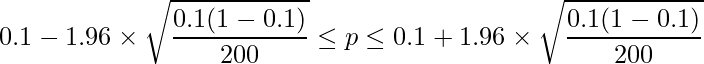
となります。
問5
①:×
標本の大きさ ![]() が十分に大きい場合には、
が十分に大きい場合には、![]() の分布は標準正規分布に従います。この場合、
の分布は標準正規分布に従います。この場合、![]() は自由度1のカイ二乗分布に従います。問題文では、「標本の大きさにかかわらず」となっているので誤りです。
は自由度1のカイ二乗分布に従います。問題文では、「標本の大きさにかかわらず」となっているので誤りです。
②:×
母集団が正規分布に従う場合には、その母集団から抽出された標本 ![]() は自由度
は自由度 ![]() のt分布に従います。問題文では、「母集団の年間所得金額分布は正規分布ではないと考えられる」となっているので誤りです。
のt分布に従います。問題文では、「母集団の年間所得金額分布は正規分布ではないと考えられる」となっているので誤りです。
③:◯
母集団がどのような分布であっても、その母集団から抽出された標本の大きさ ![]() が十分に大きい場合には
が十分に大きい場合には ![]() は標準正規分布に従います。これを中心極限定理といいます。
は標準正規分布に従います。これを中心極限定理といいます。
④:×
母集団がどのような分布であっても、その母集団から抽出された標本の大きさ ![]() が十分に大きい場合には
が十分に大きい場合には ![]() は標準正規分布に従います。問題文では、「標本の大きさ
は標準正規分布に従います。問題文では、「標本の大きさ ![]() にかかわらず」となっているので誤りです。
にかかわらず」となっているので誤りです。
⑤:×
標本の大きさ ![]() が十分小さいときに二項分布で近似できるかどうかは、母集団の分布によります。この問題の場合は二項分布での近似は適当ではないため誤りです。
が十分小さいときに二項分布で近似できるかどうかは、母集団の分布によります。この問題の場合は二項分布での近似は適当ではないため誤りです。
問6
2つのグループのサンプルサイズをそれぞれ ![]() と
と ![]() 、標本比率を
、標本比率を ![]() と
と ![]() とすると、次の式から母比率の差
とすると、次の式から母比率の差 ![]() の95%信頼区間を求めることができます。
の95%信頼区間を求めることができます。
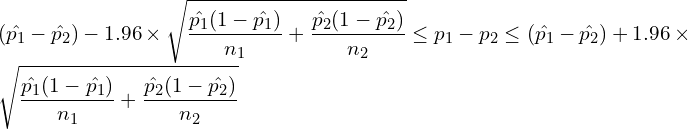
問題文より、母比率の差の95%信頼区間は

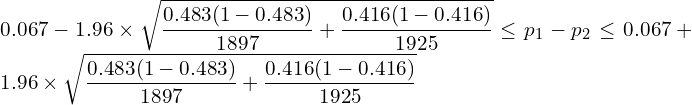
となります。この信頼区間は0をまたいでいないため、有意水準5%において帰無仮説を棄却し対立仮説を採択するという結果になります。つまり「非常に関心がある」とする者の割合が変化したと結論づけられます。
母比率の差の信頼区間については「21-6. 母比率の差の信頼区間」をご覧ください。








