- 数学ノート
- 数学的補足
標本分散の一致性と不偏性
母分散の推定量として標本分散を用いる場合に、標本分散が「一致性」及び「不偏性」を満たしているかどうかを確認してみます。
■不偏性について
標本分散 ![]() は次の式から求めることができます。
は次の式から求めることができます。
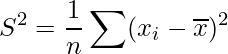
![]() は次のように展開できます。
は次のように展開できます。
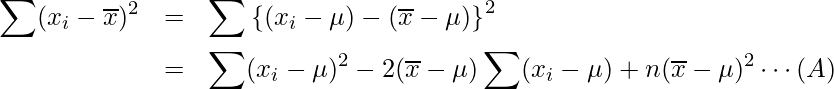
ここで、![]() の部分は次のように変形できるので、
の部分は次のように変形できるので、
(A)は次のようになります。
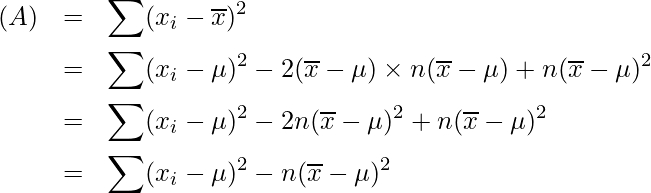
したがって、標本分散の期待値![]() は次のように展開できます。
は次のように展開できます。
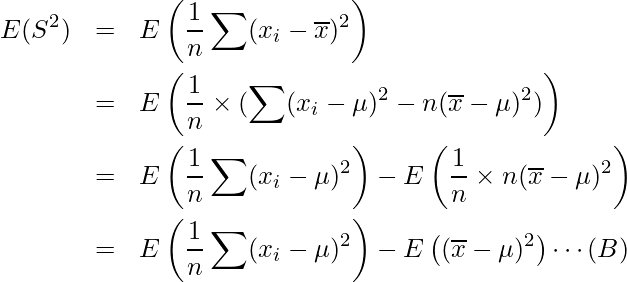
ここで、期待値の性質から![]() の部分は次のように変形ができます。
の部分は次のように変形ができます。
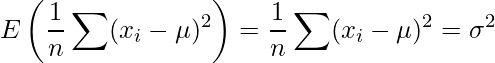
また、![]() の母分散が
の母分散が![]() のとき、標本平均の分散は
のとき、標本平均の分散は
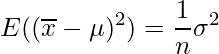
となることから、以上のことを用いて(B)は次のように展開できます。
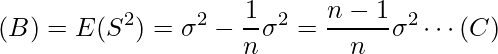
この結果から、標本分散の期待値は母分散のよりも![]() だけ小さくなることが分かります。すなわち次の式が成り立たないため、不偏性を持ちません。
だけ小さくなることが分かります。すなわち次の式が成り立たないため、不偏性を持ちません。
これは、標本分散の値を母分散の推定値として利用すると、常に母分散の値より少し小さい値となり、母分散を過小評価していることを意味します。そこで、標本分散の代わりに不偏分散を用いることで、
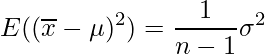
(B)の式は次のようになります。
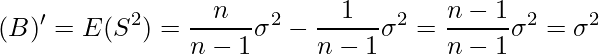
この式は、
を満たすため、不偏分散は不偏性を持つことが分かります。
■一致性について
一致性は、nが大きくなった時に推定値が真の値から外れることはほとんどないことを意味します。 直接的な証明ではありませんが、次の条件が成立すれば一致性を持つことが知られています。
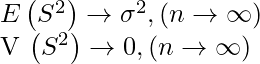
(C)の式から、![]() は次のようになります。
は次のようになります。
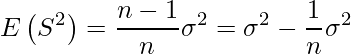
これはnが大きくなると、![]() は0に近づきます。
は0に近づきます。
次に![]() です。
少し難しいため計算過程は省きますが、実際に計算すると次のようになります。
です。
少し難しいため計算過程は省きますが、実際に計算すると次のようになります。
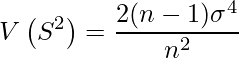
![]() は定数なので、これはnが大きくなると0に近づくことが分かります。
以上のことから、標本分散は一致性を持ちます。
は定数なので、これはnが大きくなると0に近づくことが分かります。
以上のことから、標本分散は一致性を持ちます。







