- 数学ノート
- 数学的補足
自由度
自由に値を取れるデータの数のことを自由度と言います。サンプルサイズnの標本の自由度はnであり、基本的にはサンプルサイズがそのまま自由度となります。推定量には一致性や不偏性という性質があるということは既に学びました。分散の不偏推定量は、データの標本平均からの偏差の二乗和をnで割るのではなくn-1で割ったものでした。
「n-1で割る理由」を、少し異なった観点から解説します。標本分散の計算式は
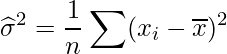
ですが、母平均![]() が分かっている場合の分散の計算式は
が分かっている場合の分散の計算式は
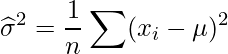
となります。真の母平均が分からないので、かわりに標本平均を母平均の代わりとして計算したものが標本分散です。標本平均![]() は、次の式で計算できます。
は、次の式で計算できます。
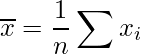
このとき、![]() は
は![]() の値で決まる推定量ですが、真の母平均でなく標本平均を代わりに使うことによって、データ1つ分のペナルティが発生してしまいます。これは、「実質的に自由に値を取れるデータ」の個数として1つ分の情報量を失ったことを意味します。
の値で決まる推定量ですが、真の母平均でなく標本平均を代わりに使うことによって、データ1つ分のペナルティが発生してしまいます。これは、「実質的に自由に値を取れるデータ」の個数として1つ分の情報量を失ったことを意味します。
例えば、サンプルサイズが3のデータから算出された標本平均が5であるとき、1つ目の値と2つ目の値は自由に取ることができます。例えば、4と6とします。すると、3つ目の値は標本平均が5となるようにしなくてはならないので、「5」しか取ることはできません。つまり、自由に値を取れるデータの個数が1つ分減ってしまった(1つ分の情報量を失った)ことになります。したがって、自由度は「3-1=2」となります。
別の見方をすると、「各データが![]() ずつの情報を出して、母平均の代わりに標本平均を計算したため、合計でデータ1個分の情報量を失っている」と考えることもできます。そのため、不偏分散の計算ではn-1で割っているのです。
ずつの情報を出して、母平均の代わりに標本平均を計算したため、合計でデータ1個分の情報量を失っている」と考えることもできます。そのため、不偏分散の計算ではn-1で割っているのです。







