統計検定2級CBT公式問題集の解説(1変数記述統計の分野)
2023/07/01
カテゴリ:統計検定
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
- 問1:相対度数の計算に関する問題
- 問2:中央値を含む階級に関する問題
- 問3:箱ひげ図と度数分布に関する問題
- 問4:幹葉図の読み取りに関する問題
- 問5:時系列の変動の性質に関する問題
- 問6:平均変化率の計算式に関する問題
- 問7:線形変換による平均・標準偏差に関する問題
- 問8:ローレンツ曲線・ジニ係数の説明に関する問題
- 問9:コレログラムの選択に関する問題
- 問10:ラスパイレス指数の計算式に関する問題
問1
相対度数分布表は、度数分布表の値をから「相対値(割合 or %)」を算出したものです。すなわち、縦の列の値をすべて足すと100%になります。
1985年の場合、85.1 +(ア)+ 0.0 + 0.0 + 0.0 + 2.1 + 0.0 = 100となることから、(ア)は100 - 85.1 - 2.1 = 12.8 (%)となります。
2017年の場合、76.6 + 17.0 +(イ)+ 0.0 + 0.0 + 0.0 + 2.1 = 100となることから、(イ)は100 - 76.6 - 17.0 - 2.1 = 4.3 (%)となります。
ちなみに、1952年から2017年にかけて、都道府県別大学数の「0校以上20校未満」の割合が減少し「20校以上40校未満」の割合が増加していることから、各都道府県において大学の数が増えてきていることが分かります。これは、最近大学が増えたなという実感とも一致するのではないでしょうか。
問2
相対度数が示されているので、累積相対度数を計算してみます。累積相対度数とは、その階級までの相対度数の全ての和(累積和)のことです。
| 階級 | 相対度数(%) | 累積相対度数(%) |
|---|---|---|
| (A)100万円未満 | 13.2 | 13.2 |
| (B)100万円以上200万円未満 | 7.2 | 20.4(13.2+7.2) |
| (C)200万円以上300万円未満 | 7.0 | 27.4(20.4+7.0) |
| (D)300万円以上400万円未満 | 6.1 | 33.5(27.4+6.1) |
| (E)400万円以上500万円未満 | 5.6 | 39.1(33.5+5.6) |
| (F)500万円以上600万円未満 | 5.5 | 44.6(39.1+5.5) |
| (G)600万円以上700万円未満 | 4.5 | 49.1(44.6+4.5) |
| (H)700万円以上800万円未満 | 4.2 | 53.3(49.1+4.2) |
| (I)800万円以上900万円未満 | 3.3 | 56.6(53.3+3.3) |
| (J)900万円以上1000万円未満 | 3.2 | 59.8(56.6+3.2) |
| (K)1000万円以上1200万円未満 | 6.0 | 65.8(59.8+6.0) |
| (L)1200万円以上1400万円未満 | 4.6 | 70.4(65.8+4.6) |
| ︙ | ︙ | ︙ |
この表から、「(G)600万円以上700万円未満」の累積相対度数は49.1%であることから、この階級以下に含まれる世帯の割合は49.1%であることが分かります。「(H)700万円以上800万円未満」の累積相対度数は53.3%であることから、この階級以下に含まれる世帯の割合は53.3%であることから、この階級以下に含まれる世帯の割合は53.3%であることが分かります。すなわち、この階級に中央値の世帯が含まれます。
問3
箱ひげ図の「東京」のデータを見てみると、次のことが読み取れます。
- 最小値は2℃以上4℃未満である
- 最大値は16℃以上18℃未満である
- 16℃以上18℃未満のデータが2つ含まれている
- 中央値は約8℃である
これらを踏まえて度数分布表を見てみます。「最小値は2℃以上4℃未満である」を満たすのは(A)(B)(C)の3つのみです。(D)は最小値が4℃以上6℃未満であり、(E)は最小値が0℃以上2℃未満であるため除外できます。
(A)(B)(C)のうち、「最大値は16℃以上18℃未満である」を満たすのは(A)(B)の2つです。(C)は最大値が18℃以上20℃未満であるため除外できます。
(A)(B)のうち、「16℃以上18℃未満のデータが2つ含まれている」を満たすのは(A)となります。
ちなみに、各データには31個の値が含まれています。小さい方から数えて(あるいは大きい方から数えて)16番目の値が中央値です。各データの中央値は(A)8℃以上10℃未満、(B)6℃以上8℃未満、(C)8℃以上10℃未満、(D)8℃以上10℃未満、(E)6℃以上8℃未満です。この結果を箱ひげ図の中央値の値と照らし合わせることもできます。
問4
1:× 最高得点は、十の位が「9」、一の位が「0」である「90点」です。
2:× 最低得点は、十の位が「4」、一の位が「0」である「40点」です。
3:○ 60点未満が不可である場合、十の位が「4」、すなわち40点台の学生と、十の位が「5」、すなわち50点台の学生が不可となります。これらに該当するのは40点台が1名(40点の1名)と50点台が6名(56点、58点、58点、58点、58点、58点の6名)の計7名になります。
4:× 上位5名の点数は、最高点である「90点」、以下「82点」、「80点」、「78点」、「78点」となります。したがって、成績Aの最低得点は「78点」となります。
5:× 最頻値とは、最も頻度が高い値(一番多く出現している値)のことです。十の位が「5」、一の位が「8」である「58点」が最も頻度が高い値であるため、最頻値となります。
問5
時系列データは一般的に「傾向変動」、「循環変動」、「季節変動」、「不規則変動」の4つの変動によって構成されている、すなわち、これら4つの変動要素に分解できると考えられています。
I:× 傾向変動は長期にわたる持続的な変化のことで、必ずしも直線で表されるわけではありません。
II:○ 季節変動は12ヶ月間(1年)で繰り返される変化のことです。時系列データから季節変動のみを抽出することで、1年の周期で値がどのように変動しているのかを知ることができます。
III:× 不規則変動は観測誤差など諸要因による変化のことです。時系列データから不規則変動と季節変動を除外することで、長期的な値の変動を捉えることができるようになります。
時系列データの詳細については「32-4. 時系列データにおける周期変動」をご覧ください。
問6
平均変化率がr(%)のとき、平成30年2月の賃金指数は次のように計算できます。
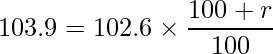
同様に、平成30年3月の賃金指数は次のように計算できます。
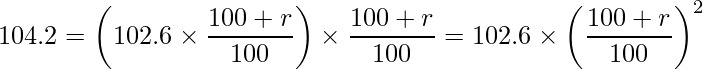
同様に、平成30年4月の賃金指数は次のように計算できます。
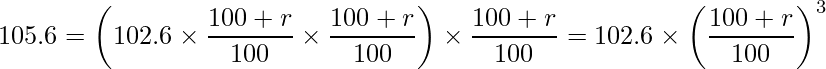
したがって、この式を整理すると
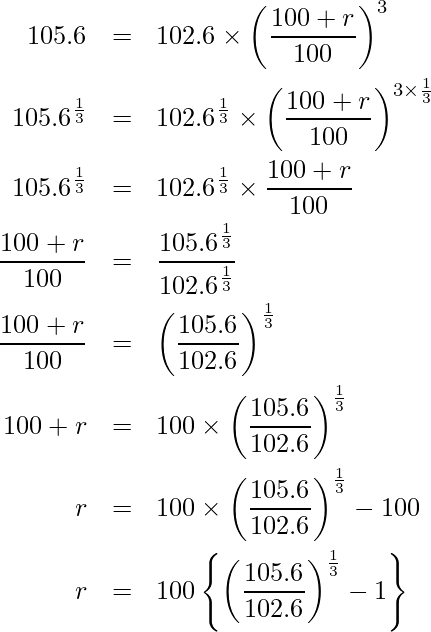
となります。
問7
華氏の値は摂氏の値を1.8倍し、32を足すことで計算されます。したがって、華氏の平均値についても摂氏の平均値を1.8倍し、32倍した値となります。
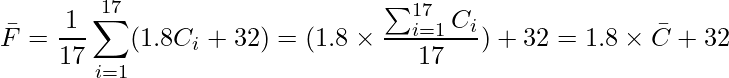
したがって、![]() となります。
となります。
華氏の標準偏差については次のように計算できます。
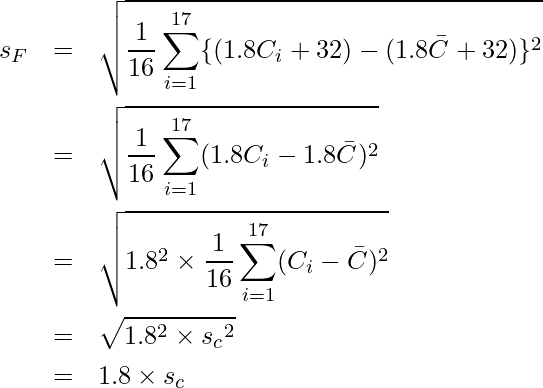
したがって、![]() となります。
となります。
問8
ローレンツ曲線とは、所得や人口の累積相対値を縦軸に、該当する世帯数や地域数の累積相対度数を横軸にとって折れ線グラフに示したものです。格差が全くないとき、ローレンツ曲線は完全平等線に沿った直線((0,0)と(1,1)を結ぶ対角線の直線)に重なります。
ジニ係数とは、ローレンツ曲線と完全平等線とで囲まれた面積を2倍した値です。ジニ係数は0から1までの値をとり、分配が平等であるほど0に近づき、不平等であるほど1に近づきます。
これらを踏まえて表の値を見てみます。
I:○ 完全平等線は第1五分位階級(20%)のとき20.0、第2五分位階級(40%)のとき40.0、第3五分位階級(60%)のとき60.0、第4五分位階級(80%)のとき80.0、第5五分位階級(100%)のとき100.0を通る直線です。表中の5カ国の五分位階級所得割合の値は、いずれも完全平等線に対して下側に凸となります。
II:× 日本、アメリカ、ドイツの五分位階級所得割合の値を見ると、アメリカの値が最も下側に凸になっている、すなわち、最も完全平等線から遠いことがわかります。したがって、アメリカが最もジニ係数が大きくなる(=不平等である)ことが予想されます。
III:○ スウェーデンと中国の五分位階級所得割合の値を見ると、中国の値がより下側に凸になっている、すなわち、より完全平等線から遠いことがわかります。したがって、中国の方がジニ係数が大きくなる(=不平等である)ことが予想されます。
ローレンツ曲線とジニ係数の詳細については「2-4. ローレンツ曲線」および「2-5. ジニ係数」をご覧ください。
問9
コレログラムとは、異なるラグについて自己相関係数を算出し、横軸にラグ、縦軸に相関係数をとったグラフのことです。自己相関係数とは、「元のデータ」と「元のデータから時間をずらしたデータ」との相関係数のことで、元データからずらした量のことをラグといいます。自己相関係数を算出することで、周期変動のあるデータに対してその周期を調べることができます。
与えられた図を見てみると、このデータは1年毎の周期があるように見えます。すなわち、ラグが12の倍数の場合の自己相関係数(元データと12、24、36…ヶ月分ずらしたデータとの相関係数)が最も高くなり、その間のラグが6、18、30…の場合の自己相関係数(元データと6、18、30…ヶ月分ずらしたデータとの相関係数)が最も低くなることが予想されます。これを満たすのは②のコレログラムになります。
コレログラムの詳細については「32-5. 自己相関」をご覧ください。
問10
基準年の購入量や取引量等を重みとして算出した価格指数のことを「ラスパイレス指数」といいます。価格と数量を次のように表すとき、ラスパイレス指数は次の式から算出できます。
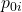 :基準年の価格
:基準年の価格 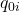 :基準年の数量
:基準年の数量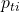 :比較年の価格
:比較年の価格 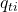 :比較年の数量
:比較年の数量
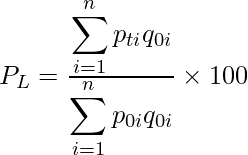
この式に表中の値を入れると次のようになります。
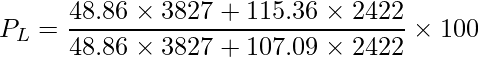
ちなみに、ラスパイレス指数とは基準時点に購入した量と同じ量を比較時点に購入した場合に、価格がどれだけ変化するかを見るための指標です。その他の指標については「32-6. さまざまな指数」をご覧ください。








