間違いやすいt検定の式
2018/02/28
カテゴリ:統計検定
統計検定2級でよく出題される母平均の検定(1標本のt検定)について、検定統計量を整理します。
1標本のt検定とは、次のような問題です。
「未知の平均![]() と、未知の分散
と、未知の分散![]() の正規母集団からn個のデータ
の正規母集団からn個のデータ![]() を抽出したとき、母平均について検定する。」
を抽出したとき、母平均について検定する。」
このとき、検定統計量![]() はどのような式となるでしょうか。
はどのような式となるでしょうか。
検定統計量のおさらい
何冊か書籍を確認したところ、多くは次のように記載されていました。(統計学の時間24-1章も同様)
(1) 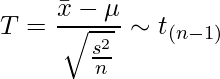
ここで、![]() は不偏分散を表します。一般に、母集団から抽出された標本を用いて母集団の推定を行う場合には不偏分散を使います(統計検定等の問題では「不偏分散」と明示されていない場合もあります)。
この式のTは帰無仮説のもとで自由度
は不偏分散を表します。一般に、母集団から抽出された標本を用いて母集団の推定を行う場合には不偏分散を使います(統計検定等の問題では「不偏分散」と明示されていない場合もあります)。
この式のTは帰無仮説のもとで自由度![]() のt分布に従うことから、t検定を行うことができます。
のt分布に従うことから、t検定を行うことができます。
検定統計量Tの式について、t分布の自由度や不偏分散をnで割っている部分がややこしくてわかりにくい、ということはないでしょうか。 もう一度Tとt分布の自由度の関係を眺めると、次の事がわかります。
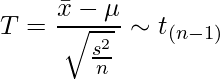
■1標本t検定のポイント
- 不偏分散を使う
- 不偏分散をnで割っている
- Tは、自由度がn-1のt分布に従う
よくある間違いとしては、次の2つが挙げられます。
- 間違い1:両方ともn-1を使ってしまう。
- 間違い2:両方ともnを使ってしまう
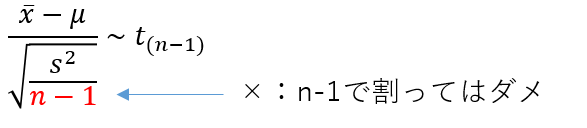

この2つはどちらも誤りです。間違えないように注意しましょう。
t検定の検定統計量は2種類ある
ここからは、ある程度t検定について整理できている人が読んでください。 いきなり読んでしまうと、t統計量を間違えて覚えてしまうかもしれませんので注意してください。
t検定の検定統計量は(1)式の表し方しかないのでしょうか。
実はそうではありません。書籍によっては、n-1で割る不偏分散![]() ではなく、nで割る標本分散
ではなく、nで割る標本分散![]() を使用することがあります。
その場合、検定統計量T'は次のようになります。
を使用することがあります。
その場合、検定統計量T'は次のようになります。
(2) 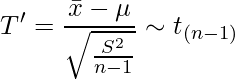
このT'も、帰無仮説のもとで自由度![]() のt分布に従います。
のt分布に従います。
TとT'を二つ並べ、見比べます。
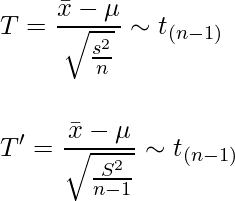
ここから、TとT'について次のようなことがわかります。
■1標本t検定のポイント(その2)
- 標本分散(nで割る分散)を使って検定統計量が定義されることもある
- 不偏分散を使用した場合はnで割るが、標本分散を使用した場合はn-1で割る
- どちらの場合でも、自由度がn-1のt分布に従う
書籍によってはどちらも載っている場合があります。定義の異なる複数の書籍を使いながら勉強する場合は、間違えないよう注意が必要です。
TとT'の関係
t検定の式には式(1)と式(2)の2通りの表し方があることがわかりました。
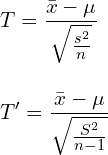
では、このTとT'は異なるものを表しているのでしょうか。
![]() と
と![]() にそれぞれの式を代入して確かめましょう。
にそれぞれの式を代入して確かめましょう。
まず、TもT'も分子は同じ![]() ですから、分母のみに注目すればよいことがわかります。
Tの分母
ですから、分母のみに注目すればよいことがわかります。
Tの分母![]() は次のようになります。
は次のようになります。
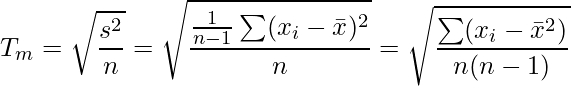
同様に、T'の分母![]() についても計算します。
についても計算します。
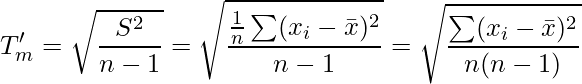
どちらも全く同じであることがわかります。 結局のところ、TもT'も同じ式について、まとめ方を変えただけのものです。
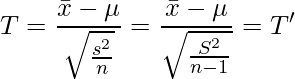
もっと勉強したい方へ
こちらの書籍がおすすめです。難しくない程度の数式を使って丁寧に説明されています。簡単すぎず難しすぎずちょうどよいレベル感です。








