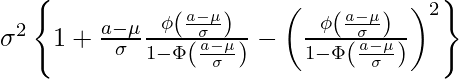切断正規分布の平均値と分散
2018/03/08
カテゴリ:数理統計
概要
平均![]() 、分散
、分散![]() をもつ正規分布
をもつ正規分布![]() について、ある点で切断したときの期待値と分散を計算します。
について、ある点で切断したときの期待値と分散を計算します。
必要な数学的知識
確率分布の基本的な性質、部分積分、置換積分
具体的な計算については、高校数学程度です。
切断正規分布の確率密度関数
正規分布![]() の確率密度関数は次の通りです
の確率密度関数は次の通りです
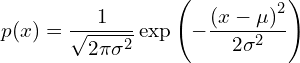
![]() の分布は次のような形状です。
の分布は次のような形状です。
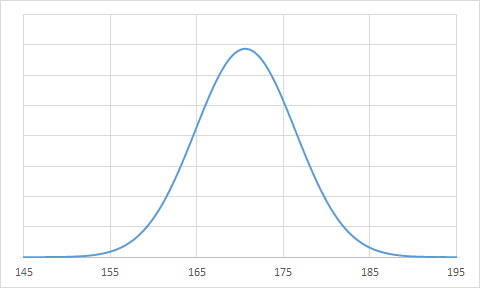
ここで![]() で分布を切断し、
で分布を切断し、![]() のみの部分からなる分布を考えます。
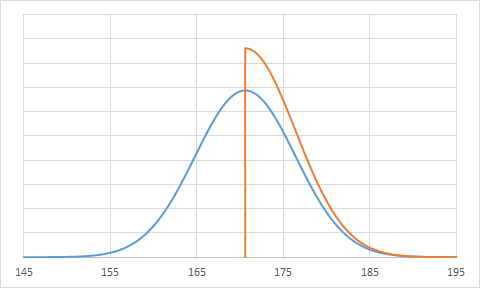
切断した分布は次のような形状です。
のみの部分からなる分布を考えます。
切断した分布は次のような形状です。
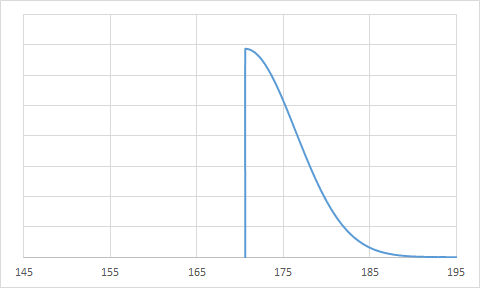
重ねて表示すると、切断した分布の確率密度の方が大きくなっています。
この分布の確率密度関数は、![]() の
の![]() での条件付き分布を計算することで求めることができます。
での条件付き分布を計算することで求めることができます。
1変数の確率分布の条件付き分布
1変数の確率分布p(x)について、![]() のような不等式の条件付き分布
のような不等式の条件付き分布![]() は次のように計算できます。
は次のように計算できます。
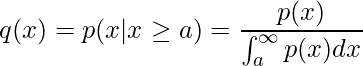
単純に、分布のa以上の部分![]() とならないことに注意しましょう。
とならないことに注意しましょう。
条件付き分布の計算方法を簡単に解説します。
![]() は確率分布であり、次の関係が成立します。
は確率分布であり、次の関係が成立します。
条件付き分布![]() も確率分布であるため、次の関係が成立している必要があります。
も確率分布であるため、次の関係が成立している必要があります。
ここで、![]() は
は![]() を
を![]() となる部分で切り取っています。
つまり
となる部分で切り取っています。
つまり![]() の定義域は
の定義域は![]() です。
このとき
です。
このとき![]() について、次のようになります。
について、次のようになります。![]() は
は![]() の累積分布関数です。
の累積分布関数です。
これは確率分布の性質「積分すると1になる」を満たさないことから、単に![]() とすることはできないことが分かります。つまり、ある定数倍して1になるように補正すればよく、その具体的な値が、
とすることはできないことが分かります。つまり、ある定数倍して1になるように補正すればよく、その具体的な値が、![]() です。
です。
これを利用して切断正規分布![]() を計算しましょう。分子は
を計算しましょう。分子は![]() そのままなので、分母を計算するだけです。
そのままなので、分母を計算するだけです。
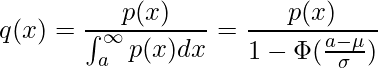
ここで、![]() は標準正規分布の累積分布関数です。
は標準正規分布の累積分布関数です。
切断正規分布の期待値
![]() が求められたので、期待値
が求められたので、期待値![]() を計算します。
を計算します。
![Rendered by QuickLaTeX.com \displaystyle E[X]=\int_a^{\infty} \frac{1}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)}\frac{x}{\sqrt{2\pi\sigma^2}}\exp \left( -\frac{\left( x - \mu \right)^2}{2\sigma^2} \right)](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-069a00c8ace1e976ddeafe21b3aa7017_l3.png)
![]() に変換します。
に変換します。
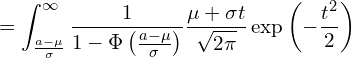
![]() の項についての積分は、分布関数を定義域で積分しているため
の項についての積分は、分布関数を定義域で積分しているため![]() となります。
となります。
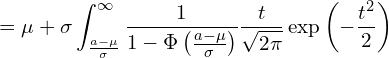
![]() であることを利用すると、積分できます。
であることを利用すると、積分できます。
![Rendered by QuickLaTeX.com \displaystyle =\mu + \sigma \left[ - \frac{1}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)}\frac{1}{\sqrt{2\pi}}\exp \left( -\frac{t^2}{2} \right) \right]_{\frac{a-\mu}{\sigma}}^{\infty}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-7b00ecbc1649ab8e37757ff53fc468ac_l3.png)
![]() であるため、
であるため、![]() の項が残ります。
の項が残ります。
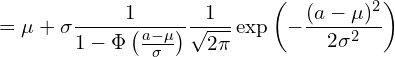
ここで、![]() の項には
の項には![]() における標準正規分布の確率密度です。
標準正規分布の確率密度関数を
における標準正規分布の確率密度です。
標準正規分布の確率密度関数を![]() と置くと、次のように書き換えることができます。
と置くと、次のように書き換えることができます。
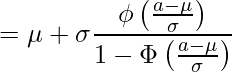
この![]() を逆ミルズ比と呼びます。
を逆ミルズ比と呼びます。
切断正規分布の分散
分散を計算します。
分散の公式![]() を使うため、
を使うため、![]() の値を求めます。
の値を求めます。
![Rendered by QuickLaTeX.com \displaystyle E[X^2]=\int_{a}^{\infty} \frac{1}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)}\frac{x^2}{\sqrt{2\pi\sigma^2}}\exp \left( -\frac{\left( x - \mu \right)^2}{2\sigma^2} \right)](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-040161eda117022c50aa5453af1fbb10_l3.png)
変数変換します。
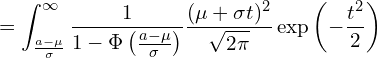
![]() を展開します
を展開します
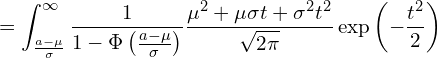
展開した項のtの次数で分割します。
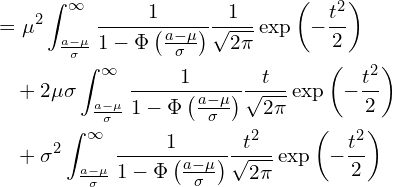
ここで第一項の積分は、確率分布の性質から1となります。
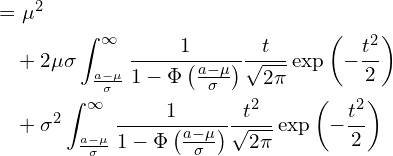
第2項は、![]() であるので、そのまま積分できます。
であるので、そのまま積分できます。
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle &=\mu^2 \\ &\quad +2\mu \sigma \left[ - \frac{1}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)}\frac{1}{\sqrt{2\pi}}\exp \left( -\frac{t^2}{2} \right) \right]_{\frac{a-\mu}{\sigma}}^{\infty} \\ &\quad +\sigma^2 \int_{\frac{a-\mu}{\sigma}}^{\infty} \frac{1}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)}\frac{t^2}{\sqrt{2\pi}}\exp \left( -\frac{t^2}{2} \right) \\ &=\mu^2 \\ &\quad +2\mu \sigma \frac{\phi \left( \frac{a-\mu}{\sigma} \right)}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)} \\ &\quad +\sigma^2 \int_{\frac{a-\mu}{\sigma}}^{\infty} \frac{1}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)}\frac{t^2}{\sqrt{2\pi}}\exp \left( -\frac{t^2}{2} \right) \\ \end{split} \end{equation*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-48e821c341477c8b7ebfce59d70afab9_l3.png)
最後の第3項です。部分積分の公式を用いて変形します。
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle &=\mu^2 \\ &\quad +2\mu \sigma \frac{\phi \left( \frac{a-\mu}{\sigma} \right)}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)} \\ &\quad +\sigma^2 \left[ - \frac{t}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)}\frac{1}{\sqrt{2\pi}}\exp \left( -\frac{t^2}{2} \right) \right]_{\frac{a-\mu}{\sigma}}^{\infty} \\ &\quad +\sigma^2 \int_{\frac{a-\mu}{\sigma}}^{\infty} \frac{1}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)}\frac{1}{\sqrt{2\pi}}\exp \left( -\frac{t^2}{2} \right) \\ &=\mu^2 \\ &\quad +2\mu \sigma \frac{\phi \left( \frac{a-\mu}{\sigma} \right)}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)} \\ &\quad +\sigma^2 \frac{a-\mu}{\sigma} \frac{\phi \left( \frac{a-\mu}{\sigma} \right)}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)} \\ &\quad +\sigma^2 \end{split} \end{equation*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-23152a919b70a0c6a9f379a012aeb23f_l3.png)
![]() が計算できたので、
が計算できたので、![]() を計算しましょう。
を計算しましょう。
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} V[X] &=\mu^2 +2\mu \sigma \frac{\phi \left( \frac{a-\mu}{\sigma} \right)}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)}+ \sigma^2 \frac{a-\mu}{\sigma} \frac{\phi \left( \frac{a-\mu}{\sigma} \right)}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)} +\sigma^2 \\ &\quad -\left( \mu + \sigma \frac{\phi \left( \frac{a-\mu}{\sigma} \right)}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)} \right)^2\\ &=\sigma^2 + \sigma^2 \frac{a-\mu}{\sigma} \frac{\phi \left( \frac{a-\mu}{\sigma} \right)}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)} - \sigma^2 \left( \frac{\phi \left( \frac{a-\mu}{\sigma} \right)}{1-\Phi \left( \frac{a-\mu}{\sigma} \right)} \right)^2 \end{split} \end{equation*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-edd36843fbc91b351c1a03d5d15bf132_l3.png)
これを整理すると、次の値になります。