一致性を簡単に判断するには？

2017/11/17

カテゴリ：数理統計

概要

この記事は、一致性を持つかどうか判断する簡単な方法を紹介します。以下では、弱一致性を単に一致性と呼びます。また、確率収束と $L_2$ 収束の関係にも簡単に触れています。

【目次】

一致性とは
一致性を証明する方法
一致性を判断する簡単な方法
使用例
解説
まとめ

一致性とは

推定量における一致性とは、何らかの母数 $\theta$ の推定量 $\hat{\theta}$ について、任意の小さな数 $\varepsilon$ で次の式が成立することです。

(1) $\begin{eqnarray*} \lefteqn{\displaystyle \lim_{n \to \infty} P \left( | \hat{\theta} - \theta | > \varepsilon \right) = 0} \end{eqnarray*}$

これは、大雑把に言って「nがとても大きい時、 $\hat{\theta}$ はほぼ間違いなく $\theta$ である。」という意味です。やや厳密性を欠いた表現ですが、大まかなイメージとしては問題ありません。

大数の法則もこの一致性と近い意味です。統計学の時間でも解説していますが、サイコロを果てしない回数投げ、出た目の平均を計算すると、真の平均である3.5以外になることはないと考えられます。

一致性を証明する方法

ある推定量が一致性を持つかは、どのように判断すればよいでしょうか。直観的には、分散が小さくなれば一致性を持ちそうに思えます。

正攻法で証明するならば、(1)式の通り $P(|\hat{\theta} - \theta|>\epsilon)$ が0になること、つまり $\hat{\theta}$ が真の値から少しでも外れる確率が0になることを示す必要があります。

一致性はチェビシェフの不等式を使って証明することが多いです。チェビシェフの不等式とは、次の不等式です。

$\displaystyle P \left( |X - E[X] | > k \right) \leq \frac{V[X]}{k^2}$

この不等式は分布によらず成立し、「分布の平均や分散」と、「平均からk以上離れる確率」の関係を記述するものです。これを使えば一致性を示すことができますが、慣れていないと少し難しく感じるかもしれませんし、時間がかかるかもしれません。

一致性を判断する簡単な方法

一致性を持つか判別するときに使える、手軽な方法を一つ紹介します。

次の二つの式が同時に成立すれば、 $\hat{\theta}$ は一致性を持つと考えられます。

(2) $\setcounter{equation}{0} \begin{eqnarray*} \displaystyle \lim_{n \to \infty} E[ \hat{\theta} ] &=& \theta \\ \end{eqnarray*}$

(3) $\begin{eqnarray*} \displaystyle \lim_{n \to \infty} V[\hat{\theta}] &=& 0 \end{eqnarray*}$

使用例

母平均 $\mu$ 、母分散 $\sigma$ の分布に従う確率変数 $X_1,X_2,\cdots,X_n$ の算術平均 $\bar{X}$ について、その平均と分散は次の通りです。 $\bar{X}$ が一致性を持つことを上で紹介した方法で確認してみましょう。

$\begin{eqnarray*} E[\bar{X}]&=&\mu \\ \displaystyle V[\bar{X}]&=&\frac{\sigma^2}{n} \end{eqnarray*}$

$E[\bar{X}]$ はnにかかわらず $\mu$ なので、式(2)の条件を満たします。また、nが大きくなると $V[\bar{X}]$ は0になり、式(3)の条件を満たします。したがって $\bar{X}$ は一致性をもつ（一致推定量である）と言えます。

解説

いくつかの難しい法則を使用しています、興味がある人は読んでください。

一般に、確率の分野で用いられる収束として次の4つがあります。

法則収束（分布）
確率収束（弱収束）
概収束（強収束）
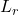$L_r$ 収束（r次の平均収束）

一致性は、推定量が確率収束するという意味です。それぞれの収束には強弱の関係があり、今回はそのうちの一つである次の関係を利用します。

ある確率変数が $L_r$ 収束するならば、確率収束する。…（A）

さらに、 $L_2$ 収束に関して、次の関係が成立します。

$\begin{eqnarray*} \left\{ \begin{array}{l} \vspace{3mm} \displaystyle \lim_{n \to \infty} E[X_n] = \mu \\ \displaystyle \lim_{n \to \infty} V[X_n] = 0 \\ \end{array} \right. \displaystyle \Leftrightarrow X_n \xrightarrow{L_2} \mu \hspace{3mm} \cdots (B) \end{eqnarray*}$

確率変数または推定量について、nが大きい時に期待値が真の値になり、分散が0になれば(B)より $L_2$ 収束します。次に（A）より、 $L_2$ 収束するなら確率収束するので、弱一致性を持つと言えます。

まとめ

チェビシェフの不等式を使わなくても、 $E[X_n]$ と $V[X_n]$ （または $E[\hat{\theta}]$ と $V[\hat{\theta}]$ ）さえ計算できれば一致性を持つかどうかが判断できることが分かります。また、分散が0に近づけば一致性を持ちそうだという直観は、実際に正しいということも分かります。

ブログ