お知らせ（2019年7月2日更新）

この記事は2017年に作成された記事です。2019年7月のアップデートで、エクセル統計に傾向スコアマッチングが搭載されました。実際に搭載された機能の詳細については、製品ページでご確認いただけます。

まえがき

エクセル統計のユーザーサポートに、「エクセル統計で傾向スコアマッチングができませんか？」というお問い合わせをいただくことがあります。 傾向スコアを用いたマッチングは観察研究データにおける処置効果の分析方法として、様々な書籍で紹介され論文にも使用されていることから、需要も増えてきているのだと思います。

残念ながら、現在のところエクセル統計には傾向スコアでマッチングを行う機能は搭載されていません。 しかし、もしもエクセル統計で傾向スコアマッチングができれば、どのような手順となるかを考えてみました。

注意

本記事は「仮に傾向スコアマッチングという機能があった場合」について考えた架空の記事です。ご注意ください。

使用するデータ

今回は、lalondeのデータを例とします。これは、1976年に実施された職業訓練プログラムと、その後の1978年における年収についてのデータです。詳細については以下の論文を参照してください。

The American Economic Review, Vol. 76, No. 4, Sept., 1986, In Orley Ashenfelter and Robert LaLonde (eds.) The Economics of Training, Vol. 2 (Cheltenham, UK:Elgar, 1996)

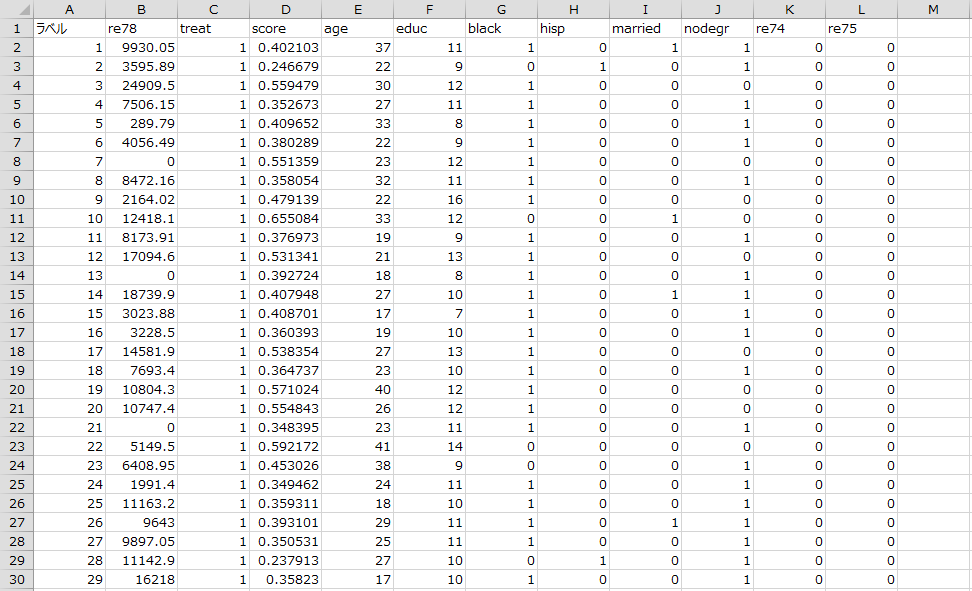
「re78」はその後の年収で、「treat」は「職業訓練プログラムの受講有無」を表す割り付け変数です。1なら処置（職業訓練プログラム）を受け、0なら処置を受けていません。「score」はロジスティック回帰分析などによって推定した傾向スコアです。「age」から「re75」は、傾向スコアを推定する際に使用した共変量です。傾向スコアマッチングにより、「treat」による「re78」の処置効果の分析を行ってみましょう。

本来であれば、傾向スコア推定のためのモデルを入念に吟味する必要があります。これは非常に大事なステップなのですが、今回はとりあえず全ての変数を用いたロジスティック回帰分析により傾向スコアを算出したという事にします。そのため、この後の分析結果で示す処置効果の推定値は真の推定値とは考えられないことに注意が必要です。変数選択の方法などモデルの吟味についてはここでは解説しませんが、例えば以下の書籍が参考になります。

『調査観察データの統計科学』（岩波書店）

分析をする

データを選択して、ダイアログから［傾向スコアマッチング］をクリックします。

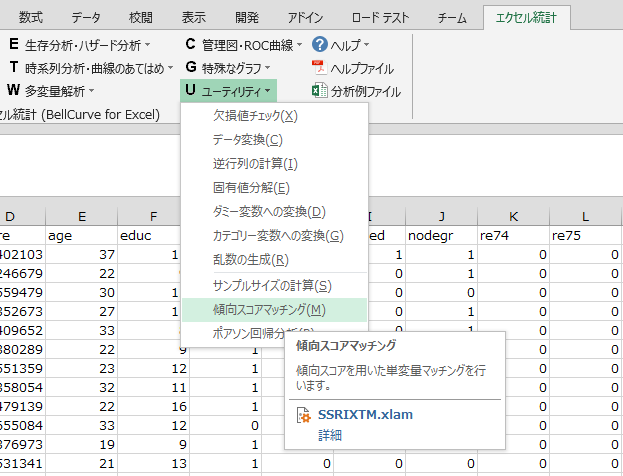
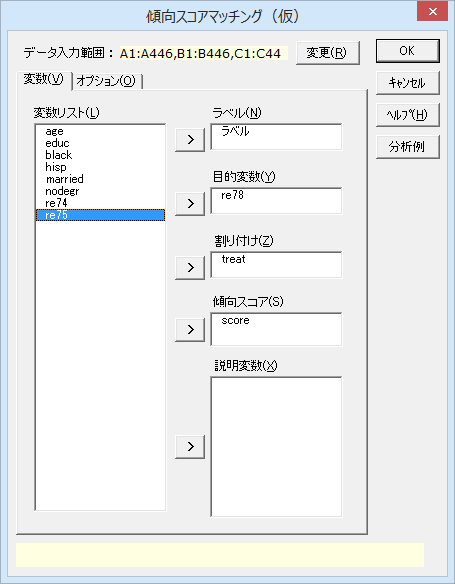
ダイアログが表示されるので、分析に必要な変数をダイアログ上で指定します。「共変量」には、傾向スコアを推定するモデルに用いた変数を指定します。

必要なオプションを指定したら、［OK］をクリックして分析を実行します。

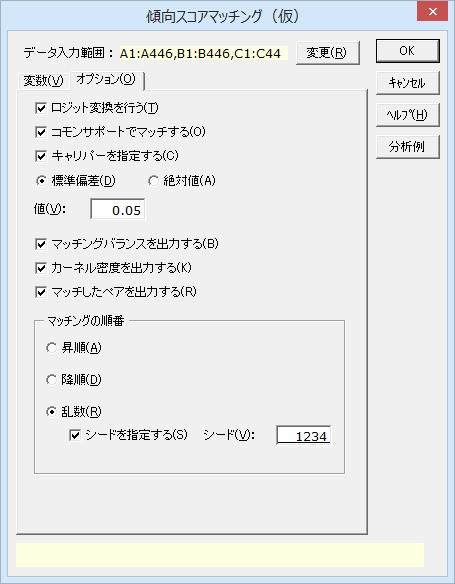
マッチング設定

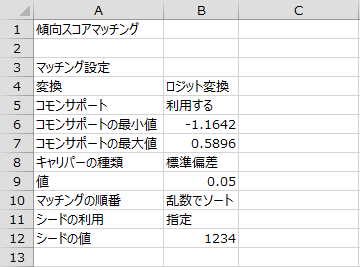
マッチングの設定が出力されます。傾向スコアをロジット変換したものをマッチングに使用しています。また、キャリパーの上限としてプールした標準偏差の0.05倍を指定しました。この値には0.25や0.1が使用されるようです。

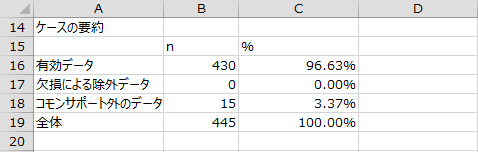
ケースの要約

分析に使用したデータの数や、分析から除外されたデータの数を確認できます。 全部で445人分のデータの中から、15人分のデータがコモンサポートの外にあるため分析対象から除外されました。

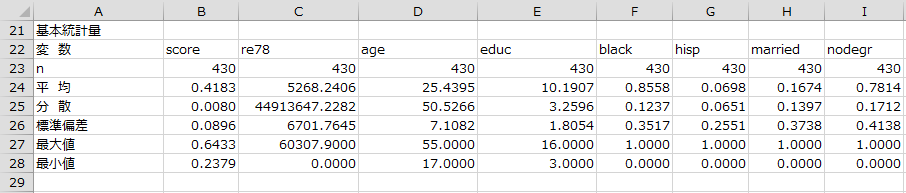
基本統計量

分析に使用した全ての変数の基本統計量が出力されます。（※出力が多いため、一部省略しています。）

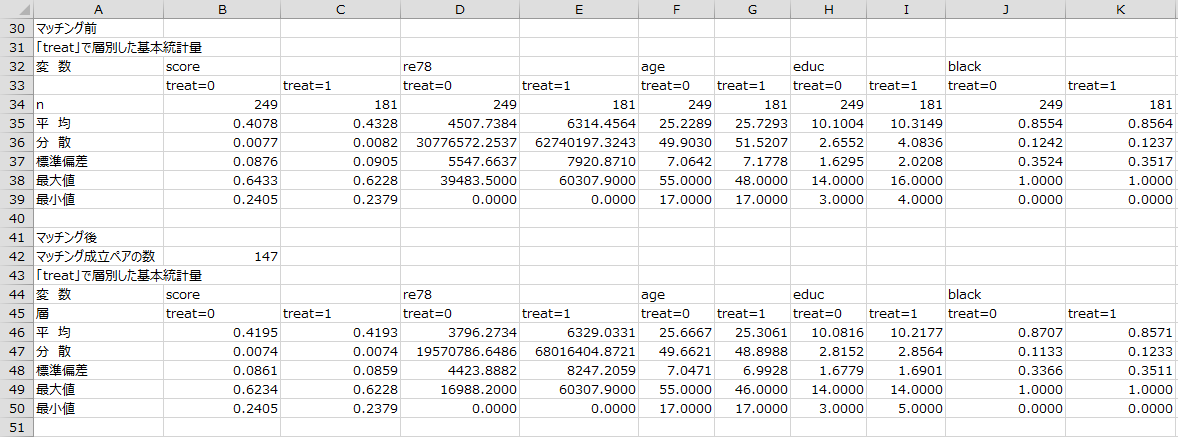
マッチング前後での層別の記述統計量

マッチング前とマッチング後において、「treat」が0と1で層別したそれぞれの基本統計量が出力されます。（※出力が多いため、一部省略しています。）今回はマッチングの実行結果として、147のペアが成立しました。 共変量については、マッチングが成立したペアでの平均や分散がマッチング前のものと比べて値が近くなっていることが分かります。例えば「educ」という共変量は、マッチング後に分散がどちらも2.8程度となり分布が似通っていると考えることができます。

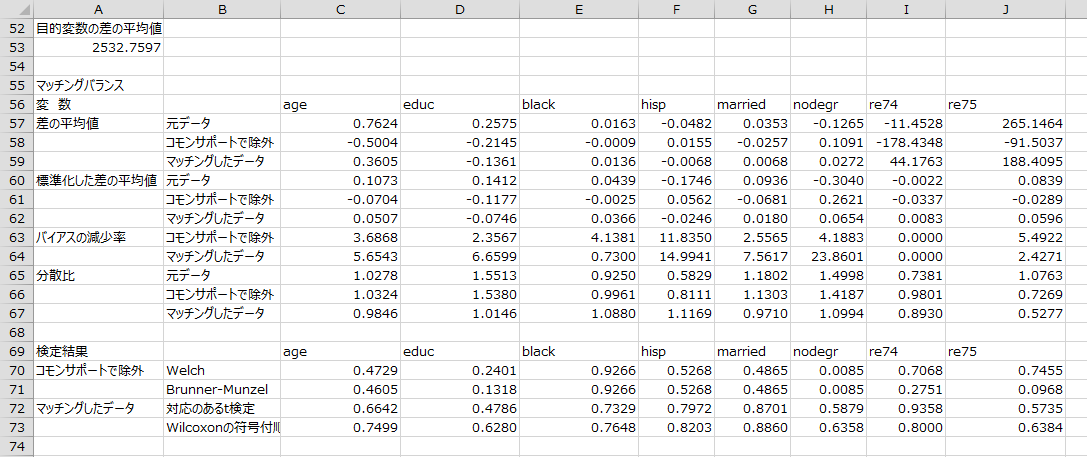
目的変数の差の平均値とマッチングバランス

目的変数の差の平均値と、マッチングバランスが出力されます。（出力が多いため、一部省略しています。）

目的変数の差の平均値が2532であることから、今回使用したモデルに基づいて調整した職業訓練プログラムの処置効果は2532と推定されます。

マッチングバランスは、割り当てで層別した各共変量差の平均値やそれを標準化したもの、そして分散がマッチングによってどの程度変化したかを表しています。差の平均値は0になるほどマッチングが上手くいっていると考えることができます。

検定結果は、マッチング前のデータについてはwelchのt検定とブルンナー=ムンツェル検定で分析した結果を、マッチング後のデータについては対応のあるt検定とウィルコクソンの符号付順位検定で分析した結果をそれぞれ出力しています。

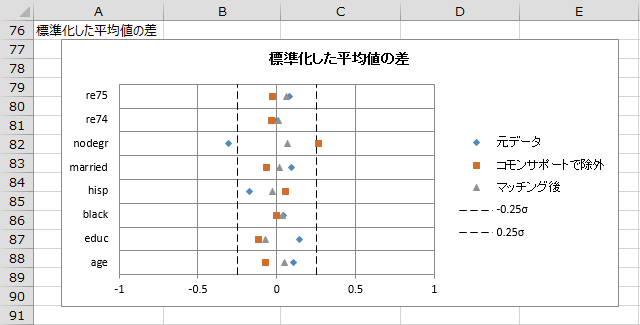
「標準化した平均値の差」グラフ

マッチングバランスで出力される「標準化した平均値の差」を、視覚的に確認するためにグラフで表したものです。 マッチング後において値が0に近づいていれば適切なモデルであると考えられますが、「re75」という変数はあまりマッチング前後で値が改善されていないようです。モデルを再検討する必要があるかもしれません。

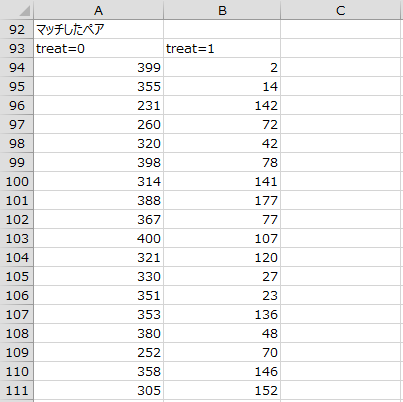
マッチングしたペア

マッチングしたペアの一覧が出力されます。どのサンプル同士がペアになったかを読み取ることができ、例えば399番の人と2番の人がペアになったことがわかります。

実際にこのような機能が搭載されるかはまだ分かりませんが、あれば便利かと思いました。他にどのようなオプションがあればより使いやすくなるか、等も考えています。例えば共変量のカーネル密度が表示されてもよさそうです。ご意見などありましたら「ご意見・ご要望」までお願いします。