因子分析─エクセル統計による解析事例

2017/04/19

カテゴリ：解析事例

※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。

分析データ

下図のデータは、自己肯定意識についての12の質問に対する200人の回答結果です。これらの質問が自己肯定意識のどのような側面をあらわしたものか、エクセル統計を用いて因子分析を行い共通因子を抽出します。

※ このデータは、実際のアンケートの結果ではなく架空のデータです。「自己肯定意識尺度（平石賢二、1990）」を参考に項目を構成しました。

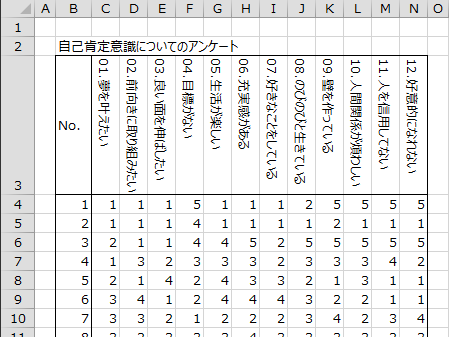
12の質問の詳細は以下の通りです。

01.自分の夢を叶えようと意欲に燃えている

02.前向きの姿勢で物事に取り組んでいる

03.自分の良い面を一生懸命伸ばそうとしている

04.自分には目標というものがない

05.生活がすごく楽しいと感じる

06.充実感がある

07.自分の好きなことがやれていると思える

08.自分はのびのびと生きていると感じる

09.他人との間に壁を作っている

10.人間関係を煩わしいと感じる

11.私は人を信用してない

12.他人に対して好意的になれない

ダイアログの設定

セル範囲「C3:N3」を選択後、メニューより［エクセル統計］→［多変量解析］→［因子分析］を選択します。

表全体のセル範囲「C3:N203」が自動で［データ入力範囲］に指定され、変数ラベルが［分析に用いる変数］に設定された状態でダイアログが表示されます。

［オプション］タブで［線形結合している変数を除いて分析する］、［因子得点を出力する］にチェックを入れます。

［因子の回転］タブで［斜交回転プロマックス法］をクリックし、［OK］をクリックします。

出力内容

出力内容の目次がハイパーリンク付きで出力されます。

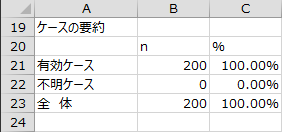
ケースの要約

欠損のない「有効ケース」と欠損のある「不明ケース」と「全体」の件数および割合が出力されます。「不明ケース」を除いた「有効ケース」が分析対象となります。このデータには「不明ケース」はありませんでした。

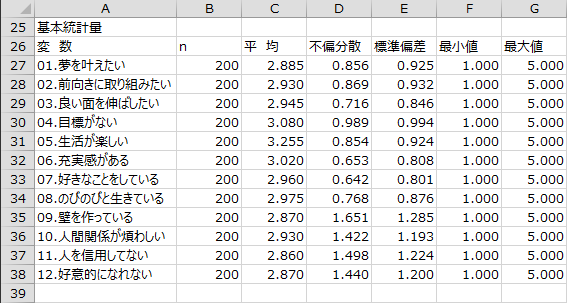
基本統計量

各変数のサンプルサイズ、平均、不偏分散、標準偏差、最小値、最大値が出力されます。

相関行列

各変数間の相関係数が行列形式で出力されます。

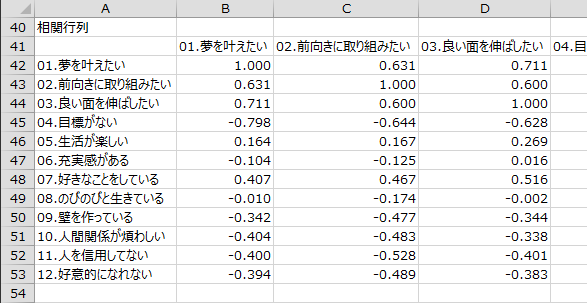
線形結合している変数・設定内容

変数間で線形結合している変数がある場合、その変数を除いて分析が行われます。このデータには線形結合している変数はありませんでした。

ダイアログで指定した設定内容と反復推定の結果が出力されます。このデータでは、最尤法による反復推定が反復回数6回で収束しました。

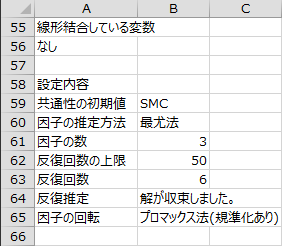
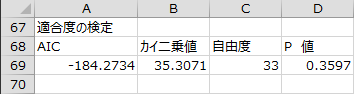
適合度の検定

因子の推定方法を［最尤法］とした場合のみ、適合度の検定の結果が出力されます。このデータの帰無仮説は「因子数3の因子分析モデルがデータに適合している」であり、もし有意水準を0.10としても帰無仮説は棄却されないので、因子数を3とする因子モデルがデータに適合していないとは言えません。

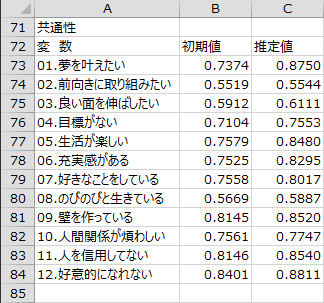
共通性

因子の共通性の初期値と推定値が出力されます。今回の場合、初期値はSMC（Squared Multiple Correlation/重相関係数の2乗）の値であり、推定値は最尤法により得られた値です。SMCは共通性の真の値の下限値を与えます。
値を見ると、初期値と推定値が近いことがわかります。また、共通性が小さい（独自性が大きい）変数もなさそうです。共通性が小さい変数がある場合、モデルを再考することがあります。

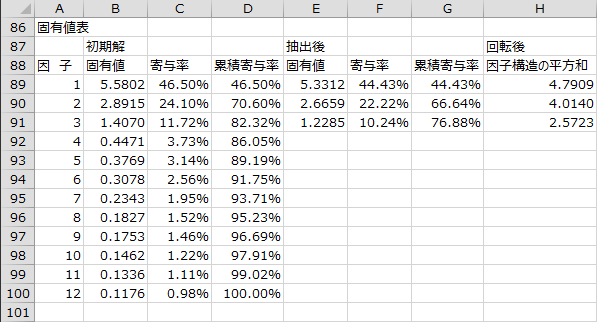
固有値表

初期解としての固有値と因子抽出後の固有値と回転後の因子構造の平方和が出力されます。
初期解は、相関行列の対角要素を共通性の初期値で置換した行列の固有値です。
抽出後の固有値は、最尤法により得られた各因子の因子負荷量の平方和です。
回転後の因子の因子構造の平方和は、あとで出力される因子構造の値を単純に平方和した値です。斜交回転を行うと因子間に相関が発生しますが、この平方和は他の因子の影響を無視した場合の寄与を表します。

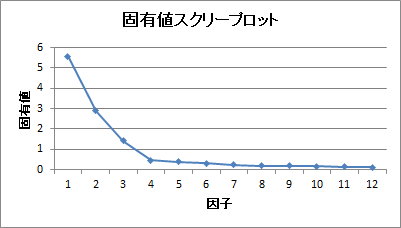
固有値スクリープロット

初期解の固有値を降順で並べた折れ線グラフが出力されます。
この折れ線で傾斜がゆるやかになっている部分のことをスクリーと言います。そして、このスクリーが始まる前までの固有値の数を因子数とすることをスクリー基準と言います。
今回の場合、「スクリー基準」と「固有値が1より大きいものの数」のいずれも因子数は3となります。

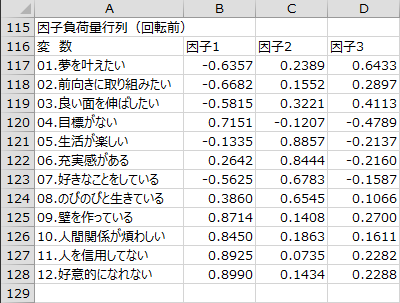
因子負荷量行列（回転前）

回転前の因子の因子負荷量が出力されます。因子負荷量は、因子が変数に与える重みを表します。この時点では因子間に相関はなく、直交しています。

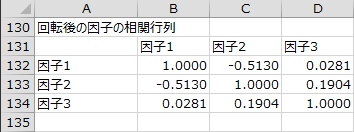
回転後の因子の相関行列

斜交回転を行った場合のみ、回転後の因子間の相関係数が行列形式で出力されます。

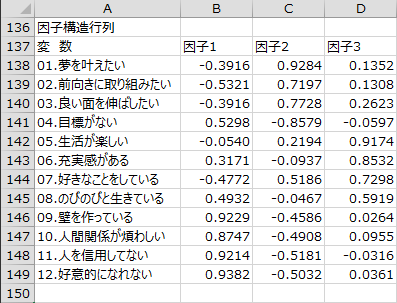
因子構造行列

斜交回転を行った場合のみ、因子構造行列が出力されます。因子構造行列は、質問項目と回転後の因子との相関係数を示したものです。相関係数なので－1から1までの値をとります。

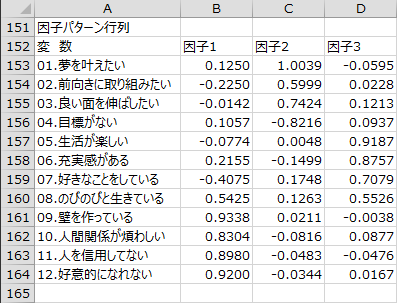
因子パターン行列

斜交回転を行った場合のみ、因子パターン行列が出力されます。エクセル統計のプロマックス法は因子パターン行列の単純化を目標に計算していますので、因子構造よりも因子パターンの方が単純化された値となります。因子の解釈には、より単純化されている因子パターンを参照します。なお、因子パターンは、－1より小さい値や1より大きい値をとることがあります。

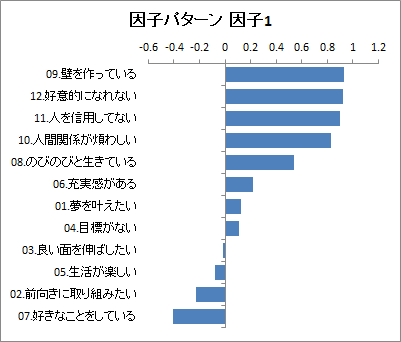
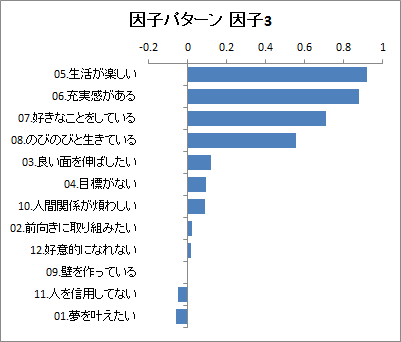
因子パターン行列のグラフ

各変数の因子パターンの値を降順で並べた横棒グラフが因子ごとに出力されます。

因子1のグラフを見ると、質問項目9?12で大きい値をとっているのがわかります。このことから因子1を「閉鎖性」と定義することにします。

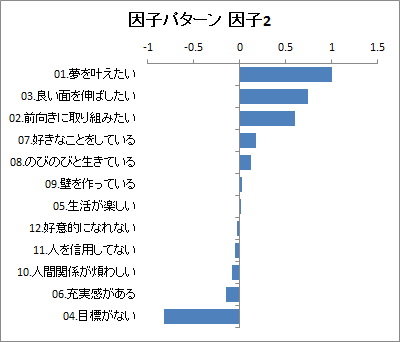
因子2のグラフを見ると、質問項目1?3で大きい値を、質問項目4で小さい値をとっているのがわかります。このことから因子2を「自己実現に対する態度」と定義することにします。

因子3のグラフを見ると、質問項目5?8で大きい値をとっているのがわかります。このことから因子3を「充実感」と定義することにします。

因子1 × 因子2の散布図

因子1と因子2の因子パターンの値をX軸とY軸にとった散布図が出力されます。質問項目が軸の付近に多く、単純構造の因子となっていることがわかります。

なお、エクセル統計では「因子1 × 因子2」の散布図しか出力されません。他の因子の組み合わせによる散布図を出力する場合は、エクセル統計のメニューから［特殊なグラフ］→［散布図 - ラベル付き・層別］をご利用ください。

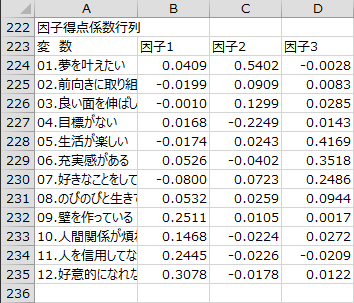
因子得点係数行列

因子ごとに因子得点係数が行列形式で出力されます。質問項目による観測値と、因子得点係数の値から因子得点が算出されます。

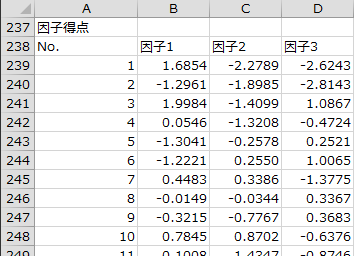
因子得点

最後に因子得点が出力されます。もともとの質問項目による観測値を、分析により推定した因子によって表した値が因子得点です。No.3の人の因子得点を見ると、因子1の値が大きく、因子2の値が小さく、因子3の値が大きいことから、「閉鎖的で自己実現に対する態度は前向きではないが充実感はある」と考えられます。

エクセル統計では、推定された因子得点と真の因子得点の誤差をできるだけ小さくすることを目的とした方法（回帰法）を用いて因子得点を推定しています。

考察

今回の場合、斜交する3つの因子が抽出され、順番に「閉鎖性」「自己実現に対する態度」「充実感」という解釈を付けることができました。
相関係数を見ると、因子1と因子2の相関係数は-0.5130、因子2と因子3との相関係数は0.1904なので、解釈に合致しています。因子1と因子3の相関係数は0.0281なので、ほぼ直交している関係にあります。
また、固有値表を見ると、他の因子の影響を無視した（各因子が直交していると想定した）値ではあるものの、因子1が4.7909、因子2が4.0140、因子3が2.5723という目安の寄与を得られます。

もし得られた因子の解釈が難しい場合、因子の推定方法や因子の数、回転の方法を変えて分析することで解釈しやすい結果が得られる可能性があります。
しかしながら、因子分析は重回帰分析のような目的変数（外的基準）はないので、どの結果が正しいとか最も優れているとかを客観的に判断することができません。変数や設定を変えて何度か試行錯誤し、その中から目的にあった結果を採択することになります。

※ 掲載している画像は、エクセル統計による出力後に一部書式設定を行ったものです。

ダウンロード

この解析事例のExcel ファイルのダウンロードはこちらから　→　example_23.xlsx

このファイルは、エクセル統計の体験版に対応しています。

ブログ