主成分分析─エクセル統計による解析事例

2017/04/19

※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。

分析データ

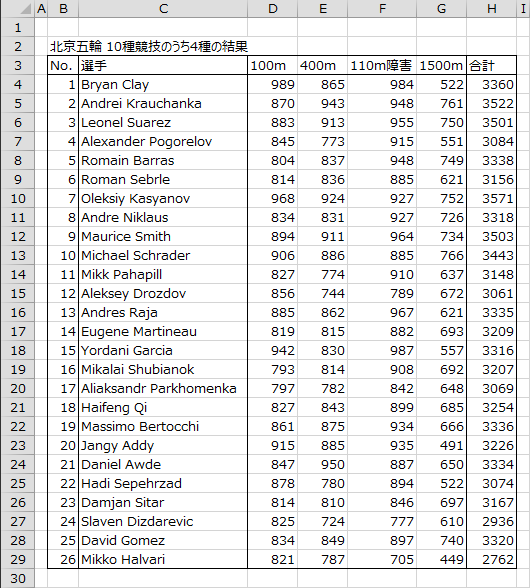
下図は、2008年8月に行われた北京五輪における陸上10種競技の結果から4種目だけ抜き出したものです。26選手について10種の競技（100m、走り幅跳び、砲丸投げ、走り高跳び、400m、110m障害、円盤投げ、棒高跳び、やり投げ、1500m）のデータが得られましたが、サンプルサイズに対して変数の数が多い場合は解析に注意が必要なため、100m、400m、110m障害、1500mの4種目のデータを抜き出しました。データは各選手の競技別の得点そのもので、10種目の合計得点の高い順に並べられています。

ダイアログの設定

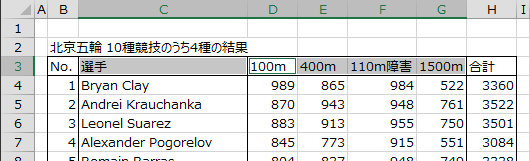
まず、データ範囲のラベルを選択します。データラベルのラベル「選手」（C3）を選択後、［Ctrl］キーを押しながら4種目のラベル「100m」「400m」「110m障害」「1500m」（D3:G3）を選択します。

メニューより［エクセル統計］→［多変量解析］→［主成分分析］を選択します。データラベルと分析に用いる変数が設定済みでダイアログが表示されます。

［オプション］タブで［線形結合している変数を除いて分析する］、［標準化したデータの分散共分散行列（相関行列）から計算する］、［主成分得点を出力する］をオンにします。［OK］ボタンをクリックして主成分分析を実行します。

出力内容

出力内容の目次がハイパーリンク付きで出力されます。

ケースの要約

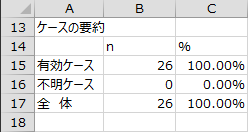
「有効ケース」、「不明ケース」、「全体」の件数および割合が出力されます。「有効ケース」が分析対象となります。

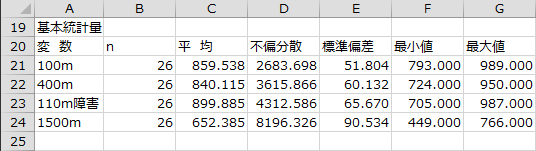
基本統計量

各変数のサンプルサイズ、平均、不偏分散、標準偏差、最小値、最大値が出力されます。

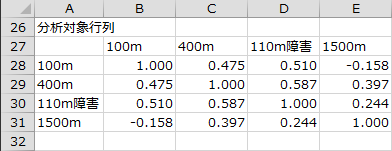
分析対象行列

ダイアログでチェックボックス［標準化したデータの分散共分散行列（相関行列）から計算する］がオンの場合、各変数間の相関係数が行列形式で出力されます。

線形結合している変数

線形結合している変数の有無が出力されます。

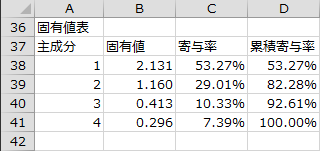
固有値表

各主成分の固有値、寄与率、累積寄与率が出力されます。

固有値：: 主成分（合成変量）の分散。; 値が1を下回る主成分は影響が少ないとみなして分析に利用しないことがあります。
寄与率：: 変数全体の分散のうち各主成分で説明される割合。; 値が 100 / 変数の個数を下回る主成分は影響が少ないとみなして分析に利用しないことがあります。
累積寄与率：: 寄与率の累計。; ここでは、主成分1と主成分2で変数全体の情報を80%以上説明できています。

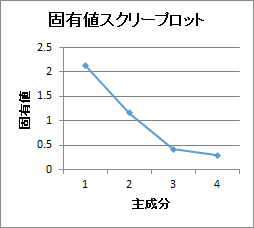
固有値スクリープロット

主成分の固有値の大きさを折れ線で示したグラフが出力されます。
この折れ線で傾斜がゆるやかになっている部分のことをスクリーと言います。そして、このスクリーが始まる前までの固有値の数を主成分数とすることをスクリー基準と言います。

固有ベクトル

各主成分の固有ベクトルが出力されます。

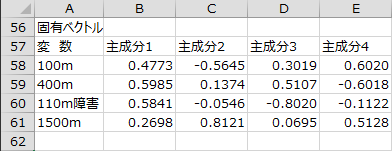
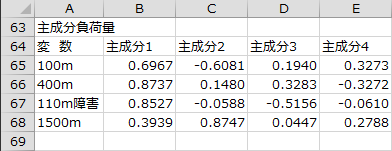
主成分負荷量

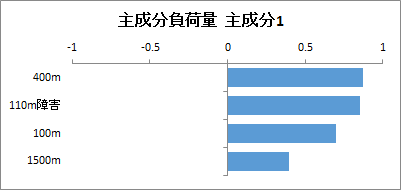
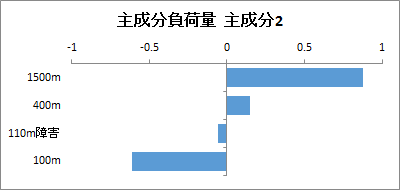
各主成分の主成分負荷量が出力されます。主成分1と主成分2については横棒グラフも出力されます。

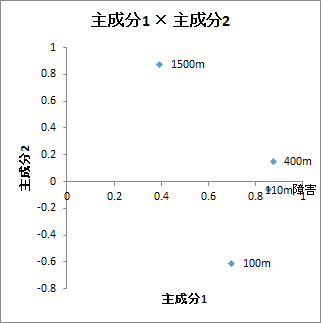
主成分1 × 主成分2の散布図

主成分1と主成分2の主成分成分負荷量による散布図が出力されます。

主成分得点

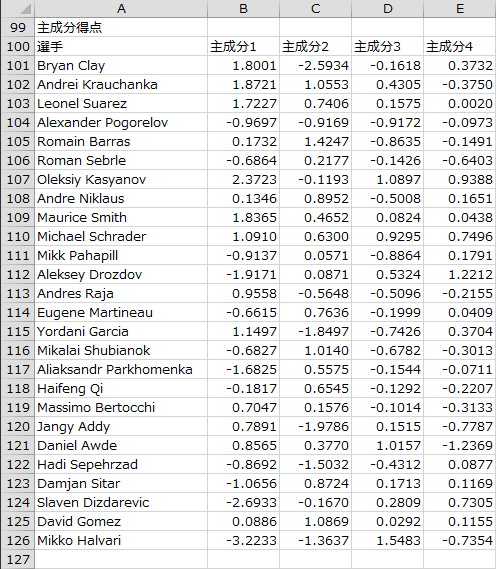
各個体について各主成分の主成分得点が出力されます。

考察

主成分1と主成分2で累積寄与率が80%を超えているので、主成分1と主成分2で今回のデータを十分説明できそうです。

主成分1の主成分負荷量を見ると、400m、110m障害、100mで大きい正の値をとっています。主成分得点を見ると、最終順位の上位選手の多くが正の値をとっています。このことから、主成分1は「総合力」という意味づけができそうです。

主成分2の主成分負荷量を見ると、1500mと400mで正の値をとり、100mで負の値となっているので、「持久力」という意味づけができそうです。

※ 掲載している画像は、エクセル統計による出力後に一部書式設定を行ったものです。

ダウンロード

この解析事例のExcel ファイルのダウンロードはこちらから　→　example_10.xlsx

このファイルは、エクセル統計の体験版に対応しています。

ブログ