※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。

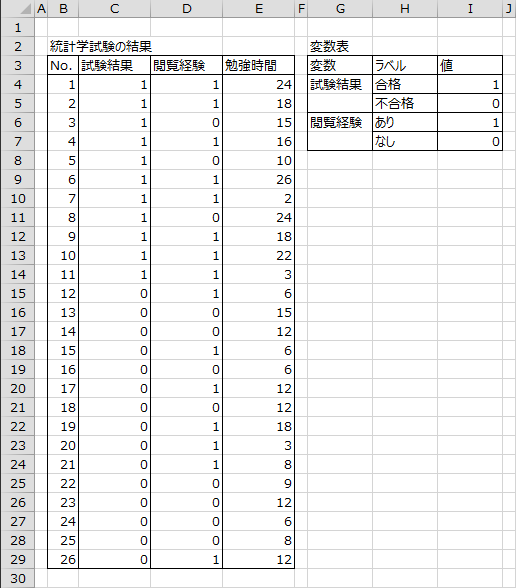
分析データ

下図のデータは、統計学の試験を26人に行った結果です。エクセル統計を用いて二項ロジスティック回帰分析を行い、統計WEBの閲覧経験と試験勉強に費やした時間が試験の合否に与える影響を調べます。

ダイアログの設定

まず、データ範囲のラベルを選択します。目的変数のラベル「試験結果」（C3）を選択後、［Ctrl］キーを押しながら説明変数のラベル「閲覧経験」「勉強時間」（D3:E3）を選択します。

続いて、メニューより［エクセル統計］→［多変量解析］→［二項ロジスティック回帰分析］を選択します。目的変数と説明変数が設定済みでダイアログが表示されます。

［変数選択］タブで「方法」を［増減法］に設定し、［変数選択の過程を出力する］をオンにします。

［オプション］タブで［線形結合している変数を除いて分析する］、［予測値を出力する］、［回帰診断の統計量を出力する］、［ROC曲線を出力する］、［ノモグラムを出力する］をオンにします。［OK］ボタンをクリックして二項ロジスティック回帰分析を実行します。

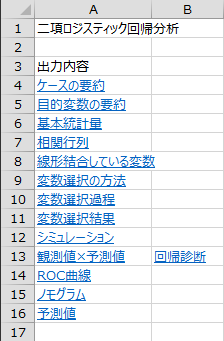
出力内容

出力内容の目次がハイパーリンク付きで出力されます。

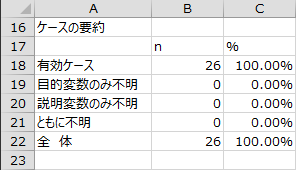
ケースの要約

「有効ケース」、「目的変数のみ不明」、「説明変数のみ不明」、「ともに不明」、「全体」の件数および割合が出力されます。「有効ケース」が分析対象となります。

目的変数の要約

目的変数が0と1の件数と割合が出力されます。

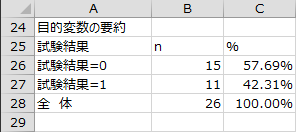
基本統計量

各説明変数の件数、平均、不偏分散、標準偏差、最小値、最大値が、目的変数の全体、0、1に分けて出力されます。

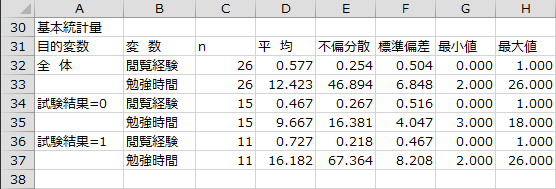
相関行列

目的変数の全体、0、1に分けて、各説明変数間の相関係数が行列形式で出力されます。

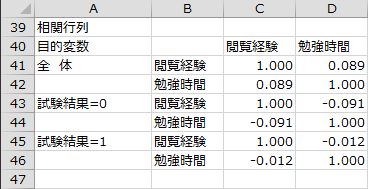
線形結合している変数・変数選択の方法

線形結合している変数の有無と変数選択の設定内容が出力されます。

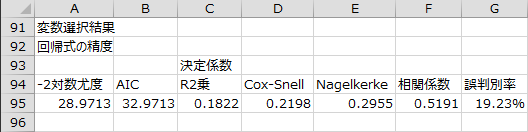
変数選択過程 - 回帰式の精度

変数選択の各ステップで回帰式の精度を表す指標が出力されます。また、変数選択の各ステップで投入または除去された説明変数のラベルも出力されます。

ステップ0で「勉強時間」が投入され、ステップ1では投入する変数がなく、ステップ1で変数選択過程が終了しました。

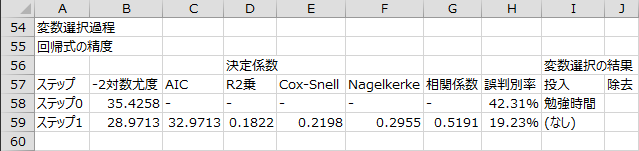
AIC（赤池情報量基準）：

複数のモデルに序列をつけるための指標。相対的に値が小さいほど精度が高いことを表す。

R2乗（寄与率）：

McFaddenのR2乗とも言う。0から1までの値をとり、1に近いほど精度が高い。式中のL(0)はスッテプ0の説明変数を含まない回帰式の対数尤度、L(β)は最終ステップの回帰式の対数尤度。

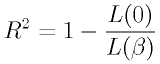
Cox-Snell R2乗：

McFaddenのR2乗は値が小さくなりすぎるため、この点を修正したもの。最大値は1にならない。nはサンプルサイズ。

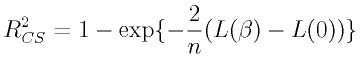
Nagelkerke R2乗：

Cox-Snell R2乗の最大値が1にならない点を修正したもの。

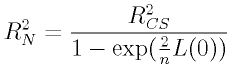
相関係数：

目的変数の観測値と予測値との相関係数。－1から1までの値をとり、1に近いほど精度が高いことを表す。

誤判別率：

有効サンプルサイズに占める、観測値と予測値が異なるケースの割合。目的変数の予測値については、0.5未満を0、0.5以上を1と分類して計算する。値が小さいほど精度が高いことを表す。

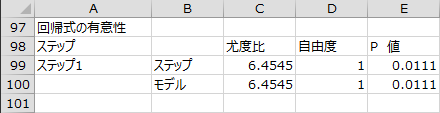
変数選択過程 - 回帰式の有意性

変数選択の各ステップで回帰式の有意性について尤度比検定を行った結果が出力されます。

ステップ1での尤度比検定の結果はP値が0.0111であり、有意水準5%で回帰式は有意であると言えます。

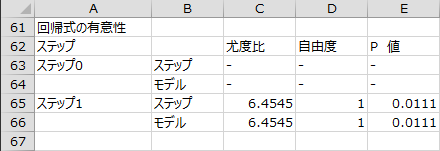
ステップ：

尤度比は前のステップとの－2大数尤度の差。前のステップからの変化の有意性を検定する。

モデル：

尤度比はステップ0との－2大数尤度の差。モデルに含まれる説明変数全体の有意性を検定する。帰無仮説は「すべての偏回帰係数は0である」。

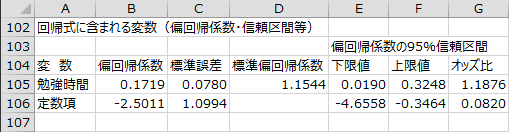
変数選択過程 - 回帰式に含まれる変数

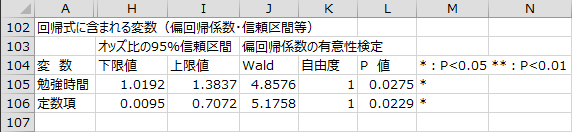
変数選択の各ステップで回帰式に含まれる説明変数の偏回帰係数や偏回帰係数の信頼区間などが出力されます。

ステップ1では、「勉強時間」のP値（0.0275）が除去の基準値（0.200）を下回ったので、「勉強時間」は回帰式から除去されませんでした。

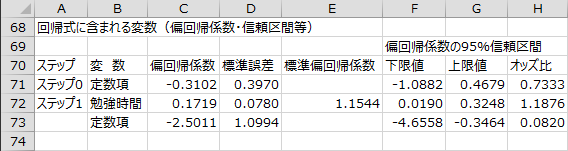
偏回帰係数：

回帰式における各説明変数の係数。

標準誤差：

偏回帰係数の推定誤差。

標準偏回帰係数：

データを標準化して分析を行った場合の偏回帰係数。各説明変数のデータの大きさの違いが考慮されないので、目的変数への影響度を比較するのに用いられる。

偏回帰係数の95%信頼区間：

偏回帰係数の95%信頼区間の下限値と上限値。信頼区間内に0を含む場合、有意性検定のP値は0.05より大きい。

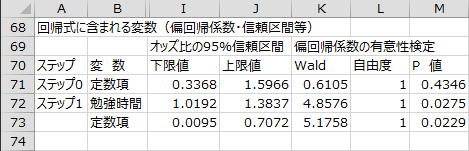
オッズ比：

偏回帰係数を指数変換（exp）した値。オッズ比が1より大きい場合、目的変数の事象が起こる確率を高め、1より小さい場合は確率を低める。

オッズ比の95%信頼区間：

オッズ比の95%信頼区間の下限値と上限値。信頼区間内に1を含む場合、有意性検定のP値は0.05より大きい。

偏回帰係数の有意性検定：

Wald統計量（カイ二乗値）を用いて、帰無仮説「偏回帰係数は0である」を検定した結果。

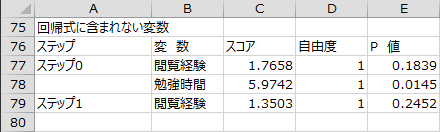
変数選択過程 - 回帰式に含まれない変数

変数選択の各ステップで、回帰式に含まれない変数を回帰式に投入した場合の有意性をスコア統計量（カイ二乗値）を用いて検定した結果が出力されます。

ステップ0では、「勉強時間」のP値（0.0145）が投入の基準値（0.200）を下回ったので、「勉強時間」が回帰式に投入されました。

ステップ1では、「閲覧経験」のP値（0.2452）が投入の基準値（0.200）を上回ったので、「閲覧経験」は回帰式に投入されませんでした。

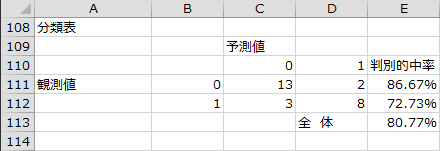
変数選択過程 - 分類表

変数選択の各ステップで、目的変数の観測値と予測値についてクロス集計を行った結果が出力されます。予測値は、0.5未満のケースを0、0.5以上のケースを1に分類しています。回帰式の精度に出力される誤判別率は、この分類表の全体の判別的中率を100%から引いた値です。

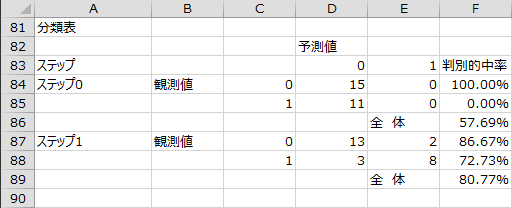
変数選択結果

変数選択の最後のステップにおける回帰式の精度と有意性、回帰式に含まれる変数、分類表が出力されます。

変数選択の結果、「勉強時間」は回帰式に投入されましたが、「閲覧経験」は回帰式に投入されませんでした。モデルの尤度比検定のP値が0.0111となり、回帰式の有意性が認められます。

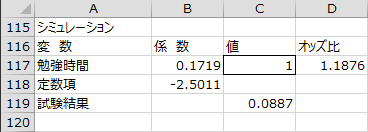
シミュレーション

「値」の欄に各説明変数の値を入力することで、求めた回帰式を用いてオッズ比と目的変数の予測値が計算されます。各セルにはExcel のワークシート関数が入力されています。

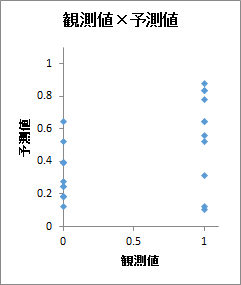
観測値×予測値・残差プロット

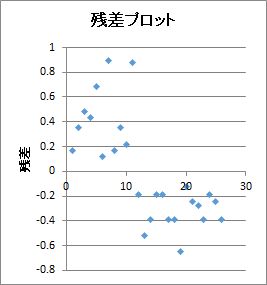
横軸に目的変数の観測値、縦軸に目的変数の予測値をとった散布図が出力されます。

また、残差プロットも出力され、縦軸が0の目盛線付近にプロットが集中していれば、モデルのあてはまりが良いと言えます。

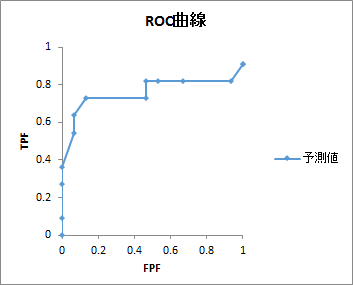
ROC曲線

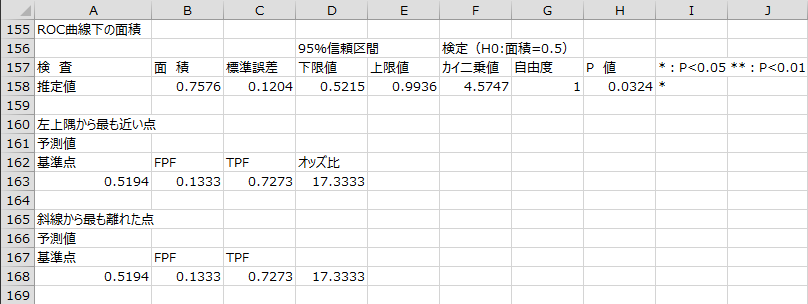
目的変数の実測値と予測値を使用したROC曲線が出力されます。曲線下の面積についての検定結果や、左上隅から最も近い点や斜線から最も離れた点についても出力されます。

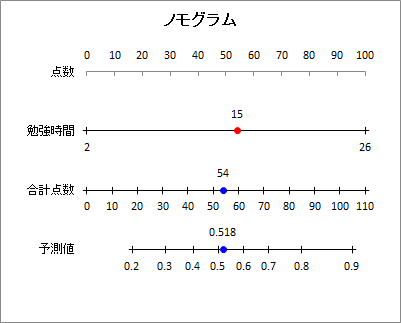
ノモグラム

ノモグラムを出力します。この値は「シミュレーション」で入力した数値と連動しています。「勉強時間」が15時間であった場合、合格する確率の予測値はおよそ52%であることがわかります。

予測値・回帰診断

目的変数の観測値と予測値、および回帰診断の値が出力されます。

回帰式の精度に出力される相関係数や分類表は、ここで出力される目的変数の観測値と予測値を用いて計算されます。

No.7と11のケースは、スチューデント化残差が2を超えており、Cookの距離も4/26=0.154を超えているので、外れ値の可能性があります。散布図ではプロットエリアで右下に位置しています。

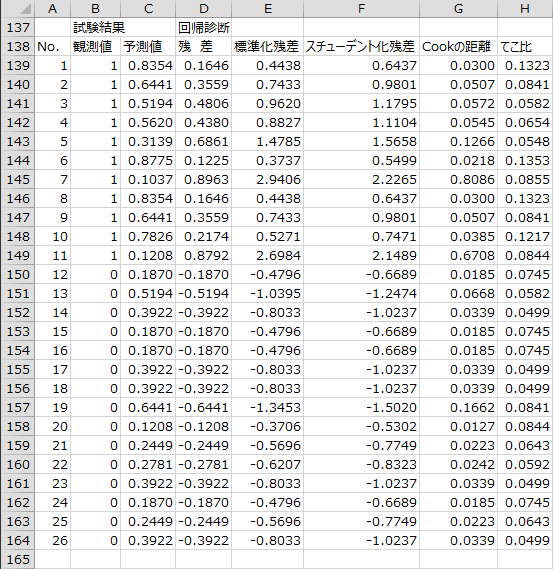
残差：

観測値から予測値を引いた値。残差プロットはこのデータを用いて作成しています。

標準化残差：

残差を標準偏差で割った値。

スチューデント化残差：

絶対値が2より大きいケースを外れ値とする場合がある。

Cookの距離：

Cookの距離が大きいとき、そのケースは結果に大きな影響を与えていることを示す。外れ値を検出する基準としては1や4/サンプルサイズなどが提案されている。標準化残差とてこ比の両方を考慮に入れた値。

てこ比：

0以上1以下の値をとり、てこ比の平均値は（説明変数の数 + 定数項の数）/サンプルサイズに等しい。外れ値を検出する基準として、てこ比の平均値の2倍や0.5などが提案されている。影響力が強いケースでも、予測値が0.1以下または0.9以上の場合は値が小さくなることがあるので注意が必要。

※ 掲載している画像は、エクセル統計による出力後に一部書式設定を行ったものです。

ダウンロード

この解析事例のExcel ファイルのダウンロードはこちらから　→　example_7.xlsx

このファイルは、エクセル統計の体験版に対応しています。

参考書籍

• 丹後 俊郎, 高木 晴良, 山岡 和枝, "ロジスティック回帰分析―SASを利用した統計解析の実際", 朝倉書店, 2013.
• 高橋 信, "すぐ読める生存時間解析―カプラン・マイヤー法/ロジスティック回帰分析/コックスの比例ハザードモデルが、よくわかる!", 東京図書, 2007.

関連リンク

• エクセル統計｜製品概要
• エクセル統計｜搭載機能一覧
• エクセル統計｜二項ロジスティック分析
• エクセル統計｜無料体験版ダウンロード