※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。

分析データ

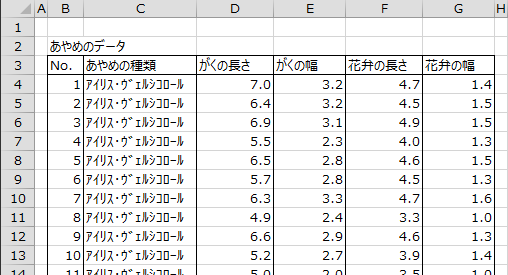
下図のデータは、あやめ科の2種類の植物、アイリス・ヴェルシコロールとアイリス・ヴィルジニカそれぞれ50個体について、がくの長さ、がくの幅、花弁の長さ、花弁の幅を測定した結果です（Fisher 1936）。

分析の目的

判別分析を用いて、2種類のあやめを判別するための判別関数を求めます。なお、エクセル統計の判別分析は正準判別分析を行います。

データラベルの選択

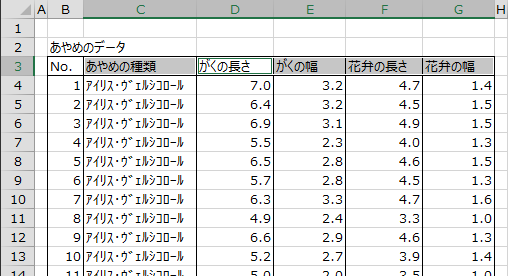
目的変数のラベル「C3」を選択後、［Ctrl］キーを押しながら説明変数のラベル「D3:G3」を選択します。

メニューの選択

メニューより［エクセル統計］→［多変量解析］→［判別分析］を選択します。目的変数と説明変数が設定された状態でダイアログが表示されます。

変数選択の設定

［変数選択］タブで「方法」を［増減法］に設定し、［変数選択の過程を出力する］をオンにします。

オプションの設定

［オプション］タブで［線形結合している変数を除いて分析する］、［BoxのM検定を出力する］、［判別得点を出力する］をオンにします。［OK］ボタンをクリックして判別分析を実行します。

出力内容

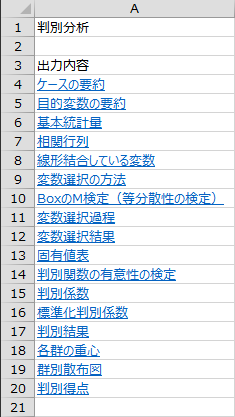
出力内容の目次がハイパーリンク付きで出力されます。

ケースの要約

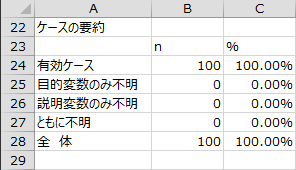
「有効ケース」、「目的変数のみ不明」、「説明変数のみ不明」、「ともに不明」、「全体」の件数および割合が出力されます。「有効ケース」が分析対象となります。

目的変数の要約

目的変数の各群の件数および割合が出力されます。

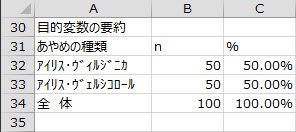
基本統計量

目的変数の群ごとに説明変数の件数、平均、不偏分散、標準偏差、最小値、最大値が出力されます。

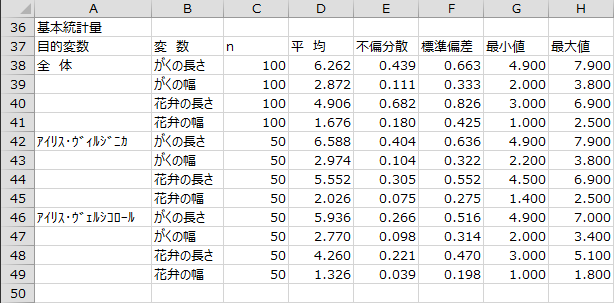
相関行列

目的変数の群ごとに説明変数間の相関係数が行列形式で出力されます。

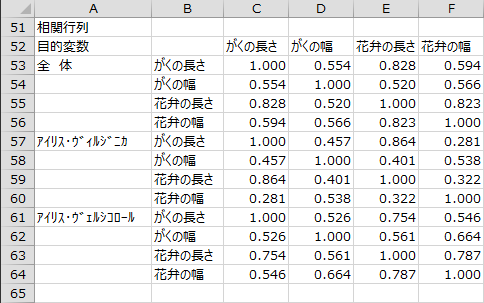
線形結合している変数・変数選択の方法

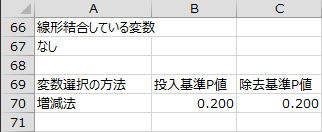
線形結合している変数の有無と変数選択の設定内容が出力されます。

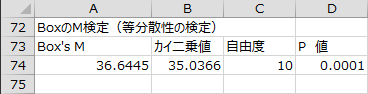
BoxのM検定（等分散性の検定）

BoxのM検定の結果が出力されます。帰無仮説は、「各群の分散共分散行列は等しい」です。

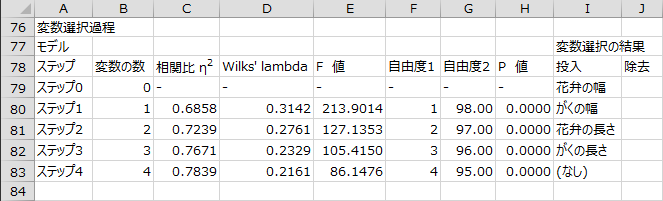
変数選択過程 - モデル

変数選択のステップごとに、変数の数、相関比、モデルの有意性検定の結果、変数選択により投入または除去された説明変数が出力されます。

相関比：

群間平方和積和行列の行列式を総平方和積和行列の行列式で割った値。0から1までの値をとり、値が大きいほど正準判別モデルのあてはまりが良いことを表します。

Wilks' lambda：

群内平方和積和行列の行列式を総平方和積和行列の行列式で割った値。0から1までの値をとり、値が小さいほど正準判別モデルのあてはまりが良いことを表します。

モデルの有意性検定：

F値の計算にはRaoのF近似を用いています。帰無仮説は「正準判別空間における3群の重心は等しい」です。

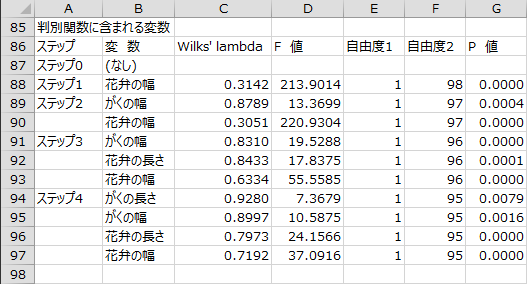
変数選択過程 - 判別関数に含まれる変数

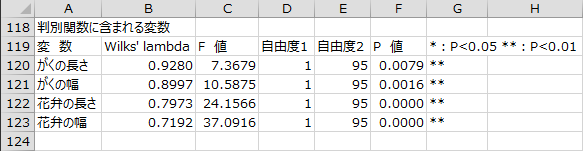
変数選択のステップごとに、判別関数に含まれる各説明変数について有意性検定を行った結果が出力されます。F値の計算にはRaoのF近似を用いています。P値が最大の説明変数のP値が「除去基準P値」（0.20）より大きい場合、その説明変数が判別関数から除去されます。

各説明変数のWilks' lambdaの積が、上述のモデルのWilks' lambdaとなります。

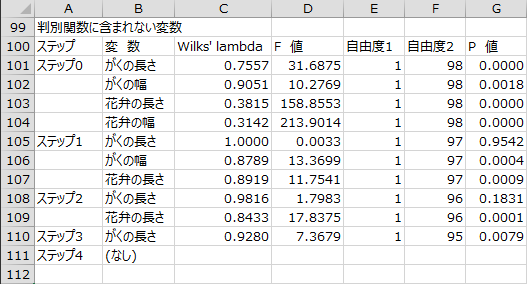
変数選択過程 - 判別関数に含まれない変数

変数選択のステップごとに、判別関数に含まれない説明変数を判別関数に投入した場合の有意性を検定した結果が出力されます。F値の計算にはRaoのF近似を用いています。P値が最小の説明変数のP値が「投入基準P値」（0.20）より小さい場合、その説明変数が判別関数に投入されます。

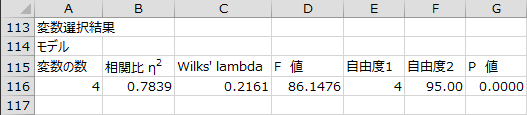
変数選択結果

変数選択の最後のステップにおけるモデル、判別関数に含まれる変数が出力されます。

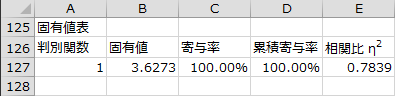
固有値表

各正準変量（各判別関数）の固有値、寄与率、累積寄与率、相関比η²が出力されます。群数－1と説明変数の数のうち、どちらか小さい方の数だけ正準変量が求められます。

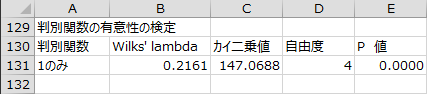
判別関数の有意性の検定

判別関数の有意性の検定を行った結果が出力されます。帰無仮説は「各群の母平均ベクトルは等しい」です。カイ二乗値の計算にはBartlettのカイ二乗近似を用いています。a+1番目以降の正準変量のP値が有意水準より大きい場合、a番目までが有効な正準変量と言えます。

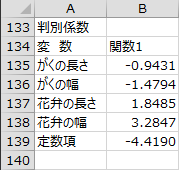
判別係数

各説明変数の判別係数が出力されます。

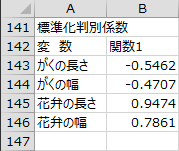
標準化判別係数

各説明変数の標準化判別係数が出力されます。標準化判別係数は、説明変数を標準化して判別分析を行った場合の判別係数で、正準変量への影響度を説明変数同士で比較するのに用いることができます。

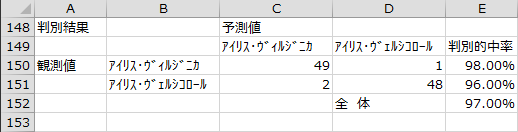
判別結果

目的変数の観測値を表側、予測値を表頭とするクロス集計表と判別的中率が出力されます。判別的中率は、正しく判別された個体数を全体の個体数で割った値です。

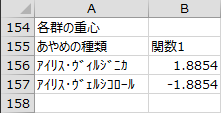
各群の重心

正準判別空間における各群の重心が出力されます。

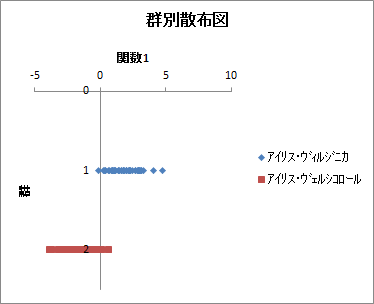
群別散布図

第1正準変量を横軸、群を縦軸にとり各個体の判別得点をプロットした散布図が出力されます。

判別得点

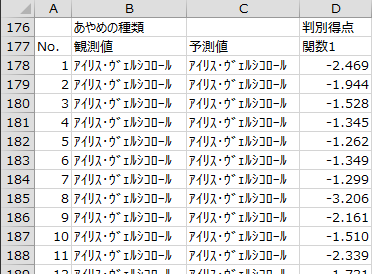
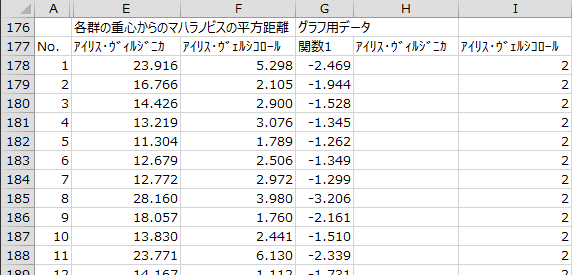
個体ごとに、目的変数の観測値と予測値、各判別関数の判別得点、各群の重心からのマハラノビスの平方距離、群別散布図作成用データが出力されます。

考察

BoxのM検定の結果、P値が0.0001なので帰無仮説が棄却されました。しかしながら、BoxのM検定はP値が小さくなりやすいので、この結果は参考値として留めておきます。

変数選択の結果、すべての説明変数が判別関数に投入されました。モデルの有意性検定のP値は0.0001未満なので、モデルのあてはまりが良いことがわかります。

判別関数の有意性の検定では、P値が0.0001未満なので帰無仮説が棄却されました。また、判別結果のクロス集計表を見ると、判別的中率が97.00%となっています。判別関数による目的変数の判別の精度が高いと言えます。

今回の判別分析で求められた判別関数は以下のようになります。

この判別関数を用いて群の判別を行う場合、判別得点が正のときは「アイリス・ヴィルジニカ」、負のときは「アイリス・ヴェルシコロール」に判別します。各群の重心とのマハラノビスの平方距離が小さい方の群に判別しても同じ結果が得られます。

※ 掲載している画像は、エクセル統計による出力後に一部書式設定を行ったものです。

ダウンロード

この解析事例のExcel ファイルのダウンロードはこちらから　→　example_8.xlsx

このファイルは、エクセル統計の体験版に対応しています。

参考書籍

• Fisher,R.A.:The Use of Multiple Measurements in Taxonomic Problems.
  Annals of Eugenics, 7: 179-188 (1936) Reproduced with permission of Cambridge University Press.
• 田中 豊, 垂水 共之, 脇本 和昌, "パソコン統計解析ハンドブック 2 多変量解析編", 共立出版, 1984.
• 柳井 晴夫, 高木 広文, "多変量解析ハンドブック", 現代数学社, 1986.

関連リンク

• エクセル統計｜製品概要
• エクセル統計｜搭載機能一覧
• エクセル統計｜判別分析
• エクセル統計｜無料体験版ダウンロード