2021年6月統計検定2級の問題の解説(その3)
2021/08/10
カテゴリ:統計検定
タグ:2021年6月
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
- 問15:母平均とサンプルサイズに関する問題
- 問16:単回帰分析に関する問題
- 問17:母比率の信頼区間と検定に関する問題
- 問18:正規分布・t分布・カイ二乗分布に関する問題
- 問19:カイ二乗検定に関する問題
- 問20:第1種の過誤の確率に関する問題
- 問21:分散分析に関する問題
- 問22:重回帰分析に関する問題
問15 [20]
母分散が既知の場合の母平均の95%信頼区間は次の式から求められます。
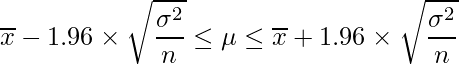
![]() は標本平均を、
は標本平均を、![]() は母分散を、
は母分散を、![]() はサンプルサイズを表します。問題文の値を用いて計算すると
はサンプルサイズを表します。問題文の値を用いて計算すると
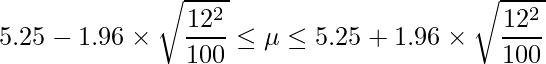
となります。
問15 [21]
[20]より母平均の95%信頼区間の幅は
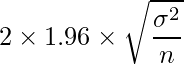
と表すことができます。問題文の条件を入れて
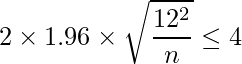
を解くと、サンプルサイズは![]() となります。
となります。
問16 [22]
最小二乗法を用いて回帰式![]() の
の![]() を定める場合、次の式を
を定める場合、次の式を![]() で偏微分した式を0とした式を使います。
で偏微分した式を0とした式を使います。
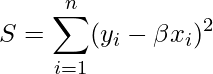
![]() で偏微分すると
で偏微分すると
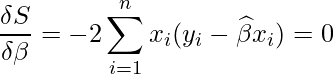
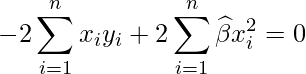
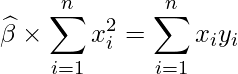
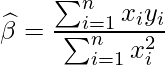
となります。偏微分を計算させるとは…。
問16 [23]
I:× 定数項を含まない単回帰モデルの場合、残差の和が0になる性質は成り立ちません。
II:○ [22]より
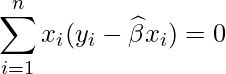
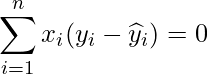
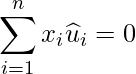
が成り立つので正しいです。
III:× Iが成り立たないので成り立ちません。
IV:× Iが成り立たないので成り立ちません。
問17 [24]
母比率の95%信頼区間は次の式から求められます。
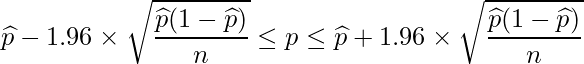
nはサンプルサイズを、![]() は標本比率を表します。問題文より標本比率は
は標本比率を表します。問題文より標本比率は![]() です。したがって、求める信頼区間は
です。したがって、求める信頼区間は

となります。
問17 [25]
(ア)![]() となる確率は次のように求められます。
となる確率は次のように求められます。
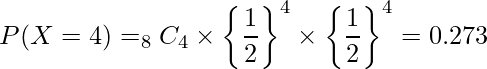
(イ)は片側検定になります。![]() となる確率(P値)は、
となる確率(P値)は、![]() となる確率と
となる確率と![]() となる確率を足したもの(7よりも極端な値が得られる確率)になります。したがって、
となる確率を足したもの(7よりも極端な値が得られる確率)になります。したがって、![]() となります。
となります。
(ウ)は両側検定になります。![]() となる確率は
となる確率は![]() となる確率と
となる確率と![]() となる確率を足したもの(7よりも極端な値が得られる確率)を2倍したものになります。したがって、
となる確率を足したもの(7よりも極端な値が得られる確率)を2倍したものになります。したがって、![]() となります。
となります。
問18 [26]
Aの式は母分散![]() を使った式であり、標準正規分布
を使った式であり、標準正規分布![]() に従います。Bの式は自由度
に従います。Bの式は自由度![]() の
の![]() に従います。
に従います。
※(イ)は正規分布の二乗和がカイ二乗分布に従うこと(詳細はこちら)から導くことができます。
正規分布、カイ二乗分布、t分布の間には次のような関係が成り立ちます。詳しくはこちらをご覧ください。
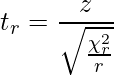
![]() は自由度
は自由度![]() のt分布に従う変数を、zは標準正規分布に従う変数を、
のt分布に従う変数を、zは標準正規分布に従う変数を、![]() は自由度
は自由度![]() のカイ二乗分布に従う変数を表します。したがって、
のカイ二乗分布に従う変数を表します。したがって、![]() 、
、![]() 、
、![]() の関係は
の関係は
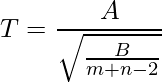
と表すことができます。
問19 [27]
まず、行と列のデータの理論値を算出します。「喫煙歴あり・心筋梗塞あり」の場合は
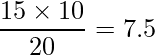
となります。同様に計算すると、「喫煙歴あり・心筋梗塞なし」の理論値は7.5、「喫煙歴なし・心筋梗塞あり」の理論値は2.5、「喫煙歴なし・心筋梗塞なし」の理論値は2.5となります。
これらの理論値と実測値を用いて![]() 値を次のように求めます。
値を次のように求めます。
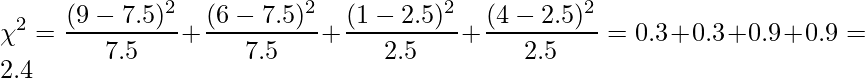
この![]() 値はm行n列のクロス集計表の場合、自由度
値はm行n列のクロス集計表の場合、自由度![]() のカイ二乗分布に従います。この問題では2行2列のクロス集計表なので、自由度1のカイ二乗分布を用いて
のカイ二乗分布に従います。この問題では2行2列のクロス集計表なので、自由度1のカイ二乗分布を用いて![]() 値の検定を行います。
値の検定を行います。
カイ二乗分布表を見ると、自由度1の場合「![]() のとき
のとき![]() 」、「
」、「![]() のとき
のとき![]() 」となっています。これら2つの値から、ものすごーくざっくりと「
」となっています。これら2つの値から、ものすごーくざっくりと「![]() が0.2くらい増加すると
が0.2くらい増加すると![]() が0.01くらい減少する」ということが分かるので、
が0.01くらい減少する」ということが分かるので、![]() になるのは
になるのは![]() を超えたあたりだと予想できます。カイ二乗検定の詳細についてはこちらをご覧ください。
を超えたあたりだと予想できます。カイ二乗検定の詳細についてはこちらをご覧ください。
問20 [28]
![]() および
および![]() はそれぞれ正規分布
はそれぞれ正規分布![]() 、
、![]() に従います。したがって、
に従います。したがって、![]() は
は![]() に従います。ここでは、帰無仮説を「
に従います。ここでは、帰無仮説を「![]() 」とするので、正規分布
」とするので、正規分布![]() を使って第1種過誤の確率を考えます。
を使って第1種過誤の確率を考えます。
まず、![]() の値を正規化すると
の値を正規化すると
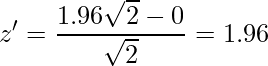
となります。標準正規分布表より![]() であることから、求める確率は0.05となります。
であることから、求める確率は0.05となります。
問20 [29]
右辺の各項が![]() となるときのzの値を求めます。[28]と逆の計算を行うわけです。
となるときのzの値を求めます。[28]と逆の計算を行うわけです。
![]() 、すなわち、
、すなわち、![]() となるときのzの値を考えます。
となるときのzの値を考えます。
標準正規分布表より![]() (※
(※![]() と
と![]() の真ん中と設定)であることから、
の真ん中と設定)であることから、
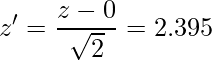
となります。
問21 [30]
ポイントは「ランダムに選んだパソコン」に対して「3種類の対策をランダムに」割り付け、さらに「測定もランダムに行う」ことです。
このようなランダムな処理が必要な理由は、系統誤差(処理の違いによる差)をなるべく小さくするためです。
問21 [31]
自由度![]() と
と![]() はそれぞれ要因(ここでは対策)の自由度と誤差の自由度を表します。詳細についてはこちらをご覧ください。
はそれぞれ要因(ここでは対策)の自由度と誤差の自由度を表します。詳細についてはこちらをご覧ください。
「要因の自由度」は因子の水準(対策の種類)の個数から1を引いたものです。したがって![]() になります。
になります。
「誤差の自由度」は「全体の自由度」から「要因の自由度」を引いたものです。「全体の自由度」は全てのデータの個数から1を引いたものなので、![]() です。したがって「誤差の自由度」は
です。したがって「誤差の自由度」は![]() になります。
になります。
問21 [32]
分散分析における信頼区間は次の式から求められます。これも統計検定2級の範囲だったとは…。
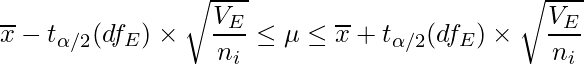
![]() は標本平均を、
は標本平均を、![]() は誤差の自由度を、
は誤差の自由度を、![]() は誤差の平均平方を、
は誤差の平均平方を、![]() はi番目の条件におけるサンプルサイズを表します。
はi番目の条件におけるサンプルサイズを表します。
[31]で求めた値を用いて誤差の平均平方を求めると![]() になります。したがって、求める信頼区間は
になります。したがって、求める信頼区間は
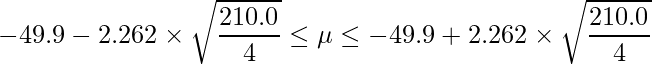
となります。
問22 [33]
偏回帰係数の有意性の検定で用いるt値は、偏回帰係数(Estimate)を標準誤差(Std. Error)で割った値です。したがって、求める値は
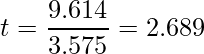
となります。
問22 [34]
1:× P値の大小は説明力の大小を表すものではありません。P値は「帰無仮説が正しいという前提において、それ以上、偏った検定統計量(この場合はt値)が得られる確率」のことです。
2:○
政令指定都市ダミーの偏回帰係数(Estimate)が「![]() 」なので、政令指定都市であれば、1人当たり社会体育施設数は0.8をかけた数(すなわち2割減)となります。
」なので、政令指定都市であれば、1人当たり社会体育施設数は0.8をかけた数(すなわち2割減)となります。
3:× 15歳未満人口の割合のP値は0.333なので、有意水準10%では棄却されません。
4:× log(1 人当たり所得)の偏回帰係数は0.519(0より大きい)なので、1人当たりの所得が高いほど1人当たり社会体育施設数が多い傾向があります。
5:× 重回帰係数は説明変数と目的変数間の相関関係(直線関係)を見るためのものであり、因果関係を見るためのものではありません。
問22 [35]
I:× モデルAにおいて「log(1 人当たり所得)」のP値は0.084です。
II:○ 自由度調整済み決定係数(Adjusted R-squared)は高いほど当てはまりの良いモデルであることを表します。モデルAは0.8362、モデルBは0.8394なので、モデルBのほうが良いモデルであるといえます。
III:○ 「回帰式の有意性の検定(F-statistic)」は、データから算出された回帰式が統計的に意味のあるものか(説明変数が目的変数を説明しているか)を検定した結果です。帰無仮説は「回帰変動は0である(偏回帰係数はすべて0である)」です。モデルAはP=4.494e–16、モデルBはP=2.2e–16であることから、両モデルにおいて説明変数にかかるすべての係数がゼロであるという帰無仮説は棄却されます。








