2標本t検定と分散分析
2019/03/14
カテゴリ:数理統計
概要
対応のない2標本t検定と分散分析の検定統計量の関係を整理します。
今回考える問題
2つの正規母集団A群とB群があり、どちらも母分散が等しく独立であるとします。この2群から、それぞれ大きさが![]() と
と![]() の標本を抽出します。
の標本を抽出します。
得られたデータより、この2群の母平均について、帰無仮説「![]() 」について統計的仮説検定を行います。
」について統計的仮説検定を行います。
検定を行う方法は2つあり、2標本t検定と一元配置の分散分析が考えられます。この二つの手法で検定統計量がどのような関係となるかを式変形により考えます。
使用する記号
A群のサンプルサイズ:![]()
B群のサンプルサイズ:![]()
A群の標本平均:![]()
B群の標本平均:![]()
A群の不偏分散:![]()
B群の不偏分散:![]()
2群全体での標本平均:![]()
i番目の個体:![]()
2標本t検定における検定統計量
まず、対応のない2標本t検定で帰無仮説「![]() 」を検定します。
このとき、検定統計量Tは次のようになります。
」を検定します。
このとき、検定統計量Tは次のようになります。
(1) 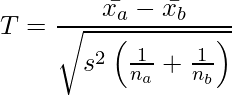
ただし、![]() はプールした分散で次のように計算されます。
はプールした分散で次のように計算されます。
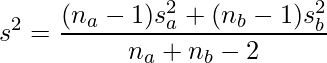
分散分析における検定統計量
次に、2群の分散分析で「![]() 」を検定します。
分散分析表を作るため、要因の平方和、誤差の平方和、全体の平方和を求めます。
」を検定します。
分散分析表を作るため、要因の平方和、誤差の平方和、全体の平方和を求めます。
要因の平方和は次の通りです。
(2) ![]()
誤差の平方和は次の通りです。
(3) 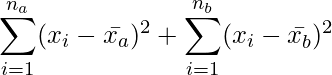
今回は用いることはありませんが、全体の平方和は次の通りです。
(4) 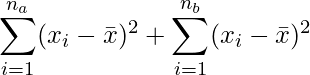
自由度はそれぞれ![]() です。
です。
続けて、平均平方を求めます。
モデルの自由度は1ですから、要因の平均平方![]() は要因の平方和と同じです。
は要因の平方和と同じです。
(5) ![]()
誤差の自由度は![]() ですから、誤差の平均平方
ですから、誤差の平均平方![]() は次のようになります。
は次のようになります。
(6) 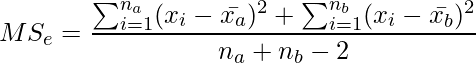
(7) 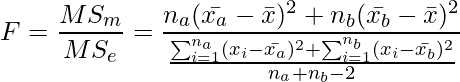
なお、最終的に分散分析表は次のようになります。カッコのついた数字が上で計算した式番号に対応し、タップすることで該当の数式にジャンプします。
TとFの関係
ここからは、先程求めたTとFの関係について考えます。
ただし、各群の偏差平方和![]() が複雑な形をしており見にくいので、それぞれ
が複雑な形をしており見にくいので、それぞれ![]() 、
、![]() とおきます。
とおきます。
なお、各群の不偏分散![]() 、
、![]() と
と![]() 、
、![]() は定義から次の関係が成立します。
は定義から次の関係が成立します。
これを用いて、T統計量を書き直します。
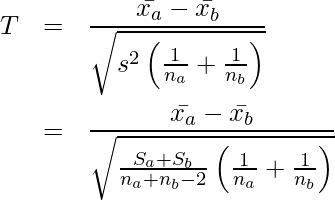
Tを二乗します。Tの変形はこれで終了です。
(8) 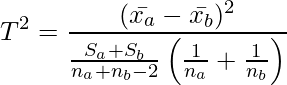
次にF統計量を変形するのですが、まず分母の![]() を書き直します。
を書き直します。
(9) 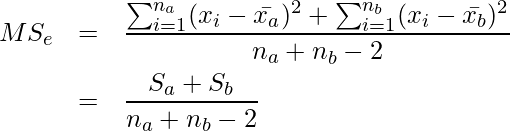
続けて分子の![]() を書き直します。全体平均
を書き直します。全体平均 ![]() と
と![]() 、
、![]() には次の関係があります。
には次の関係があります。
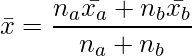
これを用いると、![]() は次のようになります。
は次のようになります。
(10) ![]()
(10)式の右辺第一項は次のように変形できます。
(11) 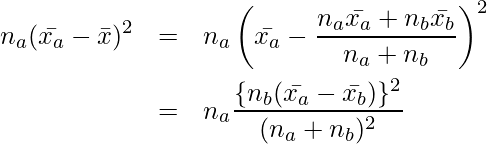
同様に、(10)式の右辺第二項も変形できます。
(12) 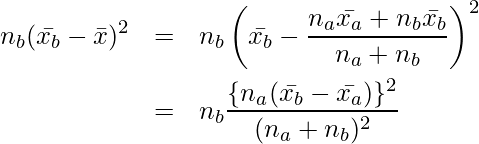
(11)と(12)の結果を用いると、![]() は次のように整理できます。
は次のように整理できます。
(13) 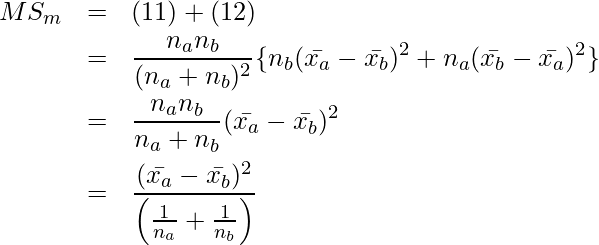
最後の変形には、次の関係を用いました。
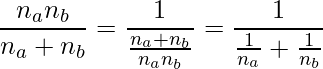
(9)と(13)の結果を用いて、F統計量は次のように書き直すことができました。
(14) 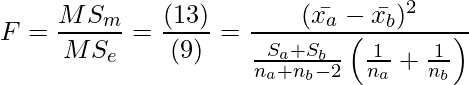
(8)式で求めた![]() と見比べると一致しており、
と見比べると一致しており、![]() であることが分かります。
つまり、2標本t検定での検定統計量を2乗すると、同じデータで分散分析を行った場合のF統計量になることが分かります。
であることが分かります。
つまり、2標本t検定での検定統計量を2乗すると、同じデータで分散分析を行った場合のF統計量になることが分かります。
補足:統計量の定義を確認する
そもそも、t分布がどのような確率変数であったかを思い出しましょう。 定義では、それぞれ独立な標準正規分布に従う確率変数Xと、自由度nのカイ二乗分布に従う確率変数Yを用いて次のような確率変数Tを作ると、Tは自由度tのt分布に従います。
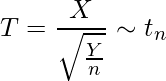
これを2乗すると、次のようになります。
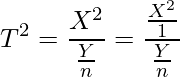
ところで、標準正規分布に従う確率変数を二乗すると、自由度1のカイ二乗分布に従います。
![]() は分子が自由度1のカイ二乗分布で分母が自由度nのカイ二乗分布ですから、F分布の定義より自由度(1,n)のF分布に従うことが分かります。
上で確かめた内容は、偶然の一致ではないということです。
は分子が自由度1のカイ二乗分布で分母が自由度nのカイ二乗分布ですから、F分布の定義より自由度(1,n)のF分布に従うことが分かります。
上で確かめた内容は、偶然の一致ではないということです。
使用例
残念ながら、この結果を用いて何か特別便利な計算ができるわけではありません。
しかし、2018年6月統計検定2級試験の大問12において、2群のデータについて対応のないt検定と分散分析の検定統計量を答える問題が出題されました。
正攻法で解くと計算に時間がかかるかもしれませんが、本記事の内容を使用して解くと次のようになります。
まず、問12(回答番号[24])は通常の通り解きます。このとき、t=1.82と答えが出てきます。次に、問12(回答番号[25])は、先に求めたt値を二乗し、![]() と計算できます。
と計算できます。








