※コラム「統計備忘録」の記事一覧はこちら※

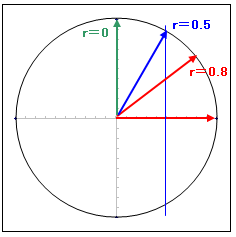
相関係数を視覚的に理解しておくと、統計学を勉強するときにとても役に立ちます。コンパスと三角定規があれば簡単にできますから、みなさんも試してみてください。

それでは、相関係数（r）が 0.8 の状態を絵にしてみます。まず、最初に半径 10cm の円を1つ描いて、円の中心から縁に向かって1本の矢印を引きます。

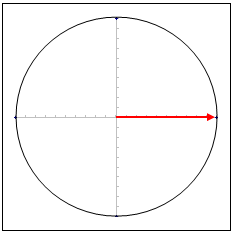
続いて、矢印の先に向かって8cmのところに、直角に交わる1本の線を引きます。

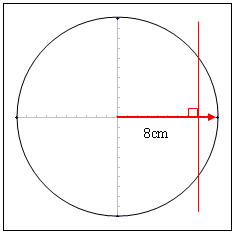
最後に、引いた線と円が交わるところに向かって、円の中心から、もう1本の矢印を引きます。

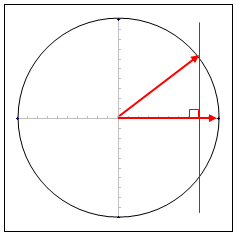
この2本の矢印の交わる角度が相関係数を表します。r=0.8 の角度は 36.8699度です。

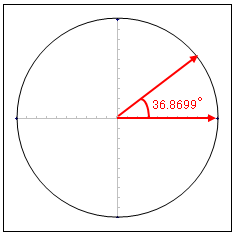
次のExcelの関数を使っても相関係数の角度を簡単に求められます。

　=DEGREES(ACOS(0.8))

2本の矢印は相関をなす2つの変数をベクトルとして表現したものです。片方の矢印の先端から、もう片方の矢印に対して垂直に交わるように線を引き、この交わったところまでの長さを射影と言います。この図では射影は8cmですね。矢印全体は 10cm ですから、8cmはベクトル全体の 8/10 (= 0.8)ということになります。2本の矢印の長さ（ベクトルの大きさ）を一緒にして射影を求めた場合、矢印の長さに対する射影の比が相関係数と一致します。

したがって、ある角度が相関係数にすると幾つになるかは、三角関数のコサイン（cosine）で求められます。60度の相関係数を知りたければExcelに次のように入力してください。

　=COS(RADIANS(60))

相関係数が 0(ゼロ) ということは角度にすると 90度、直角に交わります。統計学を勉強していると直交という言葉が良く出てきますが、直交とは r=0 のこと、無相関ということです。