母平均の差の検定（対応あり）─エクセル統計による解析事例
2017/04/19
カテゴリ：解析事例
タグ：
※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。
分析データ
下図のデータは、ある病院の眼科患者8名の眼部水晶体の厚さ（mm）を2種類の方法で測定した結果です。（出典；「医学への統計学［第3版］」朝倉書店）
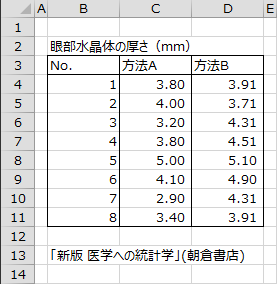
分析の目的
2種類の測定法に違いがあるかどうかを調べます。有意水準5%で両側検定を行います。
帰無仮説 H0：方法Aと方法Bの母平均は等しい
対立仮説 H1：方法Aと方法Bの母平均は異なる
データラベルの選択
セル「C3」を選択後、［Ctrl］キーを押しながらセル「D3」を選択します。
メニューの選択
メニューより［エクセル統計］→［2標本の比較］→［母平均の差の検定（対応あり）］を選択します。方法Aのデータ範囲が「検定に用いる変数1」に、方法Bのデータ範囲が「検定に用いる変数2」に指定された状態でダイアログが表示されます。
［パラメトリック検定］タブをクリックします。［母平均の差の検定（対応あり）］、［t分布］、［両側検定］にチェックを入れ、［OK］をクリックします。
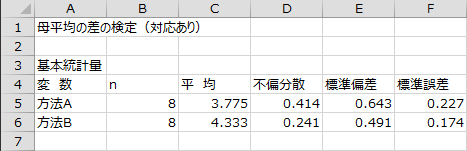
基本統計量
サンプル対の数、各群の平均、不偏分散、標準偏差、標準誤差が出力されます。
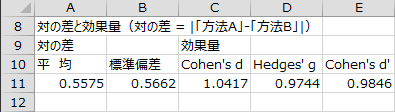
対の差と効果量
2標本の対の差の平均と標準偏差、3種類の効果量が出力されます。 Cohen's d と Hedges' g は各群の平均と標準偏差から計算した効果量です。Cohen's d' は2標本の対の差の平均と標準偏差から計算した効果量です。
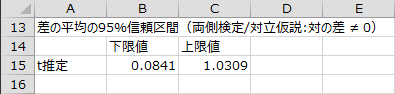
差の平均の95%信頼区間
t分布を用いて差の平均の区間推定を行った結果が出力されます。平均値の差の95%信頼区間は有意水準5%の検定結果と対応しており、検定結果が有意なら「0」を含まない信頼区間となります。
差の平均の検定
t分布を用いて2標本の差の平均を検定した結果が出力されます。
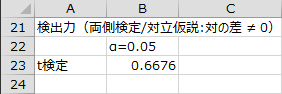
検出力
有意水準5%で両側検定を行った場合の検出力も出力されます。検定と併せて求めた検出力（事後的な検出力）は、標本平均と標準偏差が、母集団の平均と標準偏差に等しいという仮定のもとに計算しています。事後的な検出力は、追試の実験計画を立てる際の参考になります。
考察
検定の両側P値は0.0271なので、有意水準5%で帰無仮説は棄却され、2つの測定法には有意差があると言えます。ただし、このときの検出力は0.6676です。2つの測定法の差が現実にこの程度と考えられるなら、追試ではサンプルサイズを増やす必要があります。
※ 掲載している画像は、エクセル統計による出力後に一部書式設定を行ったものです。
ダウンロード
この解析事例のExcel ファイルのダウンロードはこちらから → example_4.xlsx
このファイルは、エクセル統計の体験版に対応しています。
