不偏分散の平方根は標準偏差の不偏推定量か
2017/08/04
カテゴリ:数理統計
不偏分散は母分散の不偏推定量であることが知られています。では、不偏分散の正の平方根は母標準偏差の不偏推定量、つまり「不偏標準偏差」であると言えるでしょうか。結論から言うと、「不偏推定量ではない」が答えです。以下では、正規分布の場合を例にしてそれを確認します。
最初に、不偏分散![]() の式について確認しましょう。不偏分散は次のような推定量です。
の式について確認しましょう。不偏分散は次のような推定量です。
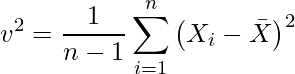
その平方根![]() は次のようになります。単純にルートを取っているだけです。
は次のようになります。単純にルートを取っているだけです。
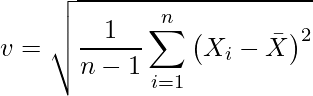
以下では、![]() 個の確率変数
個の確率変数![]() は独立に同一の正規分布
は独立に同一の正規分布![]() に従うとします。これらから、
に従うとします。これらから、![]() の母標準偏差
の母標準偏差![]() を推定することについて考えます。不偏性の定義より
を推定することについて考えます。不偏性の定義より![]() が成立すれば、
が成立すれば、![]() は標準偏差の不偏推定量であると言えます。では、
は標準偏差の不偏推定量であると言えます。では、![]() の値を具体的に計算してみましょう。
の値を具体的に計算してみましょう。
まず、カイ二乗分布の定義から、![]() を次のように変形した
を次のように変形した![]() は、自由度
は、自由度![]() のカイ二乗分布に従うことが分かっています。
のカイ二乗分布に従うことが分かっています。![]() も確率変数であると考えることができます。
も確率変数であると考えることができます。
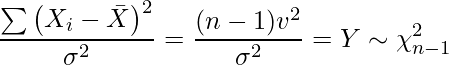
![]() と
と![]() の間には、次のような関係が成立します。
の間には、次のような関係が成立します。
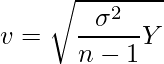
つまり、![]() を求めるためにはカイ二乗分布に従う確率変数
を求めるためにはカイ二乗分布に従う確率変数![]() について、
について、![]() の期待値を計算すればよいことが分かります。
の期待値を計算すればよいことが分かります。
自由度n-1のカイ二乗分布の確率密度関数は次の通りです。
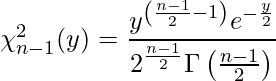
これを用いると、![]() は具体的に次のようになります。あとはこれを計算するだけです。統計検定1級や準1級を目指して勉強している方は自分でもチャレンジしてみてください。
は具体的に次のようになります。あとはこれを計算するだけです。統計検定1級や準1級を目指して勉強している方は自分でもチャレンジしてみてください。
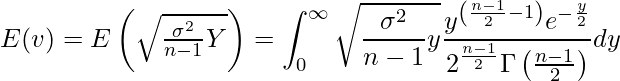
この計算は一見難しそうに見えますが、実はとても簡単に答えを求めることができます。まずは、定数![]() を積分記号の外に出してしまいましょう。
を積分記号の外に出してしまいましょう。
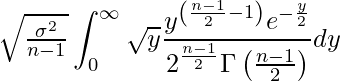
次に、![]() であることを利用して、
であることを利用して、![]() をまとめます。
をまとめます。
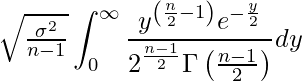
ここで、![]() の中身に注目してみます。自由度
の中身に注目してみます。自由度![]() のカイ二乗分布の確率密度関数は次の式で表されます。
のカイ二乗分布の確率密度関数は次の式で表されます。
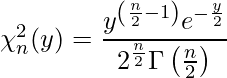
これを先程の![]() の中身とよく見比べると、分子の部分については全く同じ形をしていることが分かります。分母は
の中身とよく見比べると、分子の部分については全く同じ形をしていることが分かります。分母は![]() について定数であることを利用して、積分記号の中身を自由度nのカイ二乗分布の確率密度関数と同じ形に変形してみましょう。まず、
について定数であることを利用して、積分記号の中身を自由度nのカイ二乗分布の確率密度関数と同じ形に変形してみましょう。まず、![]() の中の分母を外に出してしまいます。
の中の分母を外に出してしまいます。
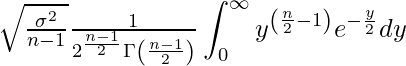
次に、![]() の分母
の分母![]() の項に等しい項だけでできた分数
の項に等しい項だけでできた分数![]() を作ります。
を作ります。
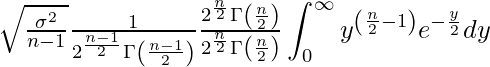
この分母だけを![]() の中に入れます。分子については他の定数項とまとめます。
の中に入れます。分子については他の定数項とまとめます。
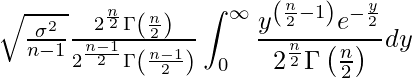
定数項部分にある2の指数乗の部分を整理します。これは![]() になります。
になります。
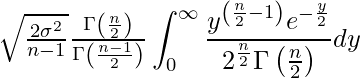
![]() の中身が自由度nのカイ二乗分布の確率密度関数と全く同じになったので、確率分布についての性質「定義域全体で積分すると1になる」を利用できます。つまり積分については無視でき、定数項が
の中身が自由度nのカイ二乗分布の確率密度関数と全く同じになったので、確率分布についての性質「定義域全体で積分すると1になる」を利用できます。つまり積分については無視でき、定数項が![]() となります。
となります。
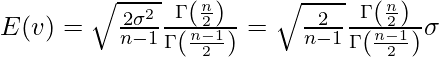
![]() の期待値は母標準偏差
の期待値は母標準偏差![]() の
の![]() 倍になることがわかります。この値は1ではないので、
倍になることがわかります。この値は1ではないので、![]() は
は![]() の不偏推定量にはなりません。
の不偏推定量にはなりません。
一般に、不偏標準偏差は不偏分散のように分布によらず成立する式として定義することはできません。








