2017年6月統計検定2級の一部問題の解説
2017/06/20
カテゴリ:統計検定
タグ:2017年6月
※統計検定2級 解説記事一覧はこちら※
2017年6月に実施された統計検定2級の問題の解説をしています。
この記事では、次の問題の解説をしています。下のリストからクリック、またはタップした問題の解説部分へジャンプします。
問9(回答番号9,10)
この問題では確率変数の定数倍の分散と、和の分散の関係式を使用します。それぞれ次のような式です。
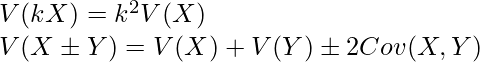
なお、問題文にXとYは独立であると書いてあるため、共分散![]() は0であることに注意しましょう。
は0であることに注意しましょう。
■回答番号9
まず、UとVの従う分布を求めます。正規分布の再生性より、UとVはそれぞれ次のような正規分布に従います。
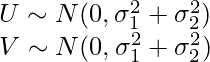
特に明記していませんが、問題文中の![]() を用いています。この時点で、UとVは同じ分布になる事がわかります。次に、UとVの相関係数を求めます。これをrとすると、相関係数の定義より次のようになります。
を用いています。この時点で、UとVは同じ分布になる事がわかります。次に、UとVの相関係数を求めます。これをrとすると、相関係数の定義より次のようになります。
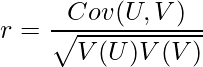
つまり![]() 、
、![]() 、
、![]() の3つが分かれば、相関係数を求めることができます。
の3つが分かれば、相関係数を求めることができます。![]() 、
、![]() については先程の結果より、次の通りです。
については先程の結果より、次の通りです。
次に![]() を求めます。UとVの和の分散について、確率変数の和の分散の関係式から次のようになります。
を求めます。UとVの和の分散について、確率変数の和の分散の関係式から次のようになります。
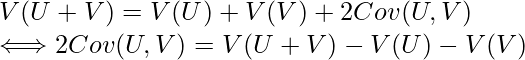
右辺の![]() と
と![]() は
は![]() であることが分かっているので、それぞれ代入します。
であることが分かっているので、それぞれ代入します。
ここで![]() 、
、![]() であることを利用します。右辺の
であることを利用します。右辺の![]() の部分に注目すると、
の部分に注目すると、![]() は次のように変形できます。
は次のように変形できます。
これを![]() 式に代入します。
式に代入します。
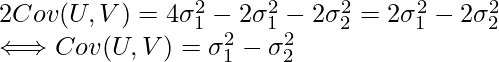
以上の事からUとVの相関係数rは次のように求められます。
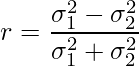
難しいように見えますが、基本的な変形のみで計算できました。
■回答番号10
各記述の正誤は次の通りです。
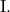 正:
正: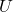 と
と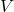 は、ともに平均0の正規分布に従います。
は、ともに平均0の正規分布に従います。 正:
正: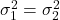 のとき、前問より
のとき、前問より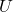 と
と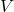 の共分散
の共分散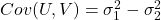 は0となるため、
は0となるため、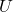 と
と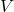 は互いに独立になります。
は互いに独立になります。 正:前問の途中でも触れましたが、
正:前問の途中でも触れましたが、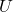 と
と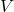 はともに
はともに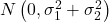 に従うことが分かっています。また、明らかに
に従うことが分かっています。また、明らかに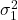 や
や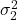 がどのような値でも成立します。
がどのような値でも成立します。








