※コラム「統計備忘録」の記事一覧はこちら※

エクセル統計には重回帰分析の出力にトレランスとVIFが含まれています。この2つの数値は多重共線性をチェックするために用います。

多重共線性には正確多重共線性と準多重共線性があります。正確多重共線性とは、相関行列の逆行列が求められないことを言います。逆行列を計算できない原因は、変数の個数がデータの数より多いか、変数間に1次結合があるかのどちらかです。逆行列を求められないので重回帰分析は途中で打ち切られます。

さて、本来、変数間には1次結合があるはずなのに、測定誤差などによる僅かな誤差があって1次結合が崩れ、逆行列が求まることがあります。これが準多重共線性の起こっている状況です。重回帰分析の結果もでてきますが、結果の信頼性は低く、データが少しでも増えたり減ったりする度に、偏回帰係数が大きく変化してしまう可能性があります。

通常、トレランスが 0.1以下の場合に準多重共線性があると考えます。トレランスの計算方法は統計用語集に難しそうに書いてありますが、単純にすると次の通りです。

　トレランス＝1－決定係数
　
この決定係数は、重回帰分析に用いようとした説明変数の中から、変数1個を目的変数にし、残りの変数を説明変数にして重回帰分析を行うと得られます。決定係数が 0.9（重相関係数に直すと約 0.95）以上と変数間が強い相関を示すとき、トレランスは 0.1 以下になります。

VIFの訳語は分散拡大係数です。トレランスが分かれば VIF の計算は簡単です。VIF が 10 以上なら、準多重共線性を疑うということになります。

　VIF＝1／トレランス

エクセル統計には、多重共線性に対しもう1つ機能があります。重回帰分析のダイアログに「線形結合をしている変数を除いて分析する」というオプションがあり、これをチェックしていると、1次結合による正確多重共線性がある場合、1次結合している変数の片方をプログラムが勝手に除いて重回帰分析を行います。

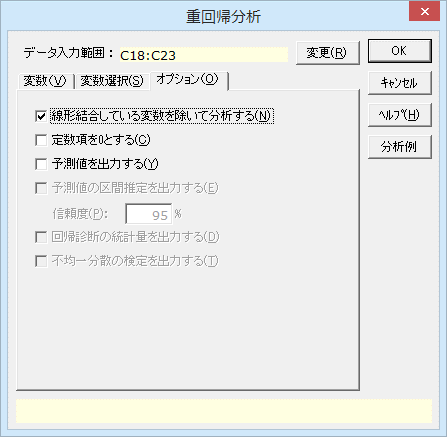
このオプションをチェックしておけば、「逆行列が求められません」というメッセージは表示されません。