※コラム「統計備忘録」の記事一覧はこちら※

今回は、フィッシャーの3原則の最後、局所管理について書きます。

局所管理 local control
1919年、フィッシャーは、ピアソンからゴールトン生物測定研究室の主任統計学者としての採用の申し出を受けましたが、ピアソンに反発していたフィッシャーは申し出を断り、ロンドン郊外にあるロザムステッド農事試験場の研究員になりました。1933年にピアソンの後任としてロンドン大学の優生学の教授になるまで、この農事試験場で研究を続け、その研究成果が「実験計画法」としてまとめられて1935年に出版されました。

さて、フィッシャーが着任するまで、ロザムステッド農事試験場では、肥料の効果を調べるために、広い農地いっぱいに1つの肥料を撒いて小麦やジャガイモなどの収量を測っていました。肥料の種類の数だけ農地を必要としていました。そこで、フィッシャーは農地を小区画（これをブロックと呼びます）に分けて、区画内では列ごとに異なる肥料を与えるよう実験方法を改めます。ブロック内のどの列にどの肥料を与えるかはランダムに割り付けます。こうすることで、1つの農地から、複数の肥料について反復のあるデータが得られるようになり、実験の効率も精度も上がりました。この実験方法は「乱塊法」と名づけられています。

＜乱塊法による3肥料・3ブロックの割り付け例＞

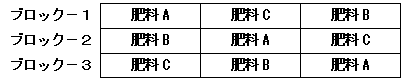
乱塊法によって、データの反復を得ることに成功しましたが、もう1つ問題が残っています。広い農地のことですから、ブロックによって土壌や空気の流れが異なり、収量に影響するかもしれません。ブロックによる誤差（収量のばらつき）が大きくなってしまうと、一元配置分散分析では肥料間の差を検出できなくなる可能性があります。そこでフィッシャーはブロックも分散分析の要因に加えることで、ブロックによる誤差を全体の誤差から分離し、分析の精度を上げることにしました。この分析手順を追ってみましょう。

まず、肥料ごとに1列にまとまるように収量のデータを次のように整理します。

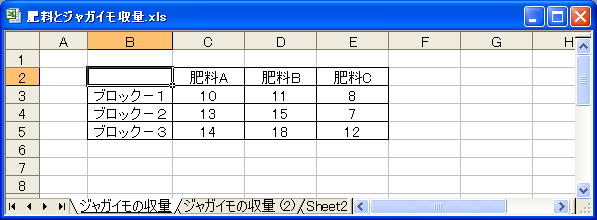
このデータを肥料の違いだけを要因とした一元配置分散分析にかけてしまうと、結果は次の通りです。

Excelの分析ツールによる一元配置分散分析の結果

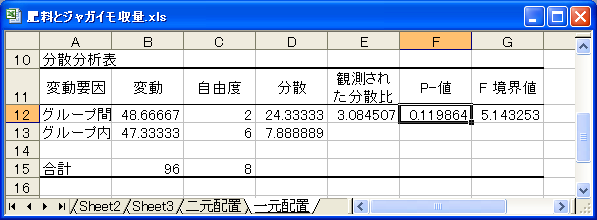
「グループ間（肥料の違い）」の行の「Ｐ-値」は「0.119864」で5%の有意水準で判断すると、肥料間の収量の差は有意ではないという結論になってしましいます。グループ内（普通の統計ソフトなら、ここは誤差と表示されます）の変動にブロックによる収量のばらつきが含まれ、誤差変動が大きくなってしまっているからです。

それでは、同じデータを「繰り返しのない二元配置分散分析」にかけてみます。分析結果は次の通りです。

Excelの分析ツールによる繰り返しのない二元配置分散分析の結果

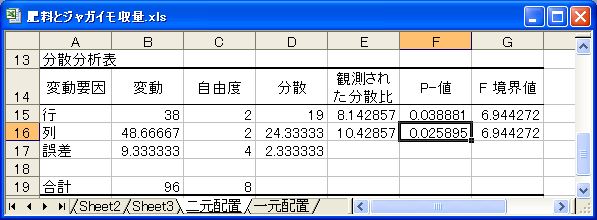
変動要因の「列」が肥料の違いになります。変動要因の分散を誤差の分散で割った分散比（F値）の「P-値」は「0.025895」ですから、５％の有意水準で「肥料により収量が異なった」と判定できます。一元配置分散分析とは異なる結論です。

なぜ、結論が変わったかというと、一元配置分散分析のときの誤差の変動からブロック（「行」のところです）による変動が取り除かれたことで（47.33333 - 38＝9.33333）、誤差の分散が小さくなったからです。肥料の分散は一元配置分散分析と同じで、誤差の分散だけ小さくなったため、分散比としては二元配置分散分析の方が大きくなり有意判定が変わったのです。

話が長くなりましたが、局所管理とは「データのブロック化とブロックを要因に加えた分散分析」のことです。例えば、人間を対象にした実験であれば、実験要因の違いよりも、被験者の個人差の方が大きくなることがままあります。このような場合は、被験者をブロックとして実験計画を組み、分散分析で被験者も要因に加えて分析すればよいのです。