※コラム「統計備忘録」の記事一覧はこちら※

実験計画法や分散分析の本を読むと、必ずといってよいほど「フィッシャーの3原則」について書かれています。実験の精度を高めるために、どのように実験計画を組むべきかを説いたものです。実験系以外の人も覚えておいて損はないので簡単に触れておきます。

第1の原則 ： 反復　replication
第2の原則 ： 無作為化　randomization
第3の原則 ： 局所管理　local control

なお、今回のコラムには確率誤差と系統誤差という2つの誤差が出てきます。2つの誤差の意味が分からない方は、「誤差の問題」の記事に書いていますので事前にお読みください。

反復　replication
1つ目は反復の原則です。1つの処理（分散分析の「水準」のこと）について2つ以上の測定を行うことです。それぞれの処理において1回の測定では、測定値に違いがあっても、系統誤差（処理の違いによる差）なのか、それとも確率誤差なのかは判断できません。そこで各処理ごとに複数回測定をして確率誤差のばらつきを調べます。確率誤差のばらつきが分かれば真の平均のとりうる範囲を推測でき、この範囲よりも系統誤差が大きければ、処理によって違いがあるという判断をくだせます。反復の原則とは確率誤差を知るためのものです。

この反復のことを分散分析では「繰り返し」と言います。1つの処理について測定を繰り返した回数を「繰り返し数」と言います。

Excelの分析ツールには「分散分析：繰り返しのない二元配置」と「分散分析：繰り返しのある二元配置」があります。例えば3品種の稲と2種類の肥料という2要因による収量の比較実験を行う場合、6通りの水準の組み合わせがあります。この6通りの組み合わせについて1つずつしか測定しないときは、「分散分析：繰り返しのない二元配置」を使用します。各品種については繰り返し数が2（肥料の種類）、各肥料については繰り返し数が3（稲の品種）になるので、それぞれの要因効果（主効果）を検出できます。しかし、品種と肥料の組み合わせから生じる効果（交互作用）は検出できません。

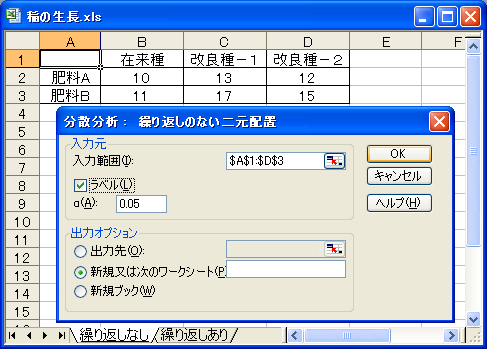
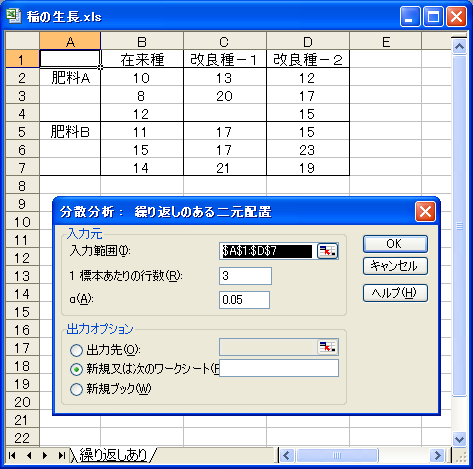
すべての組み合わせで繰り返し数が2以上であれば「分散分析：繰り返しのある二元配置」を利用できます。交互作用も検出できます。このとき気をつけることは、すべての繰り返し数を揃えることです。繰り返し数（分析ツールでは1標本あたりの行数）が不揃いになると要因間に相関が生じ（これを直交性が失われると言います）、実験の結果がどちらの要因の影響によるものか判断ができなくなります。統計ソフトの多くは繰り返し数が不揃いな場合に対応した計算方法を備えていますが、Excelの分析ツールでは繰り返し数の不揃いは不可です。

ちなみに「繰り返しのない二元配置分散分析」を英語にすると two-way factorial ANOVA without replication 、もしくは、two-way ANOVA without replicationとなります。「繰り返しのある二元配置分散分析」は without 以下を外します。紛らわしいことに「反復測定（重複測定） repeated measurement」による分散分析というのもありますが、この場合の反復は別の意味です。ご注意ください。

さて、次回は無作為化の原則について書く予定です。