※コラム「統計備忘録」の記事一覧はこちら※

単回帰分析と重回帰分析を別々のものと思い込んでいる人もいますが、Excelの分析ツールでは両者を「回帰分析」と一纏めにしているように、説明変数1個だけの重回帰分析が単回帰分析ということになります。しかし、単回帰分析で求めた重相関係数と（単）相関係数は必ずしも一致しません。

重相関係数は、実際に観測された目的変数の値と、重回帰式をあてはめて計算した推定値（理論値）との相関係数です。重相関係数の二乗を決定係数、もしくは、寄与率と言います。Excelの分析ツールでは「重決定　R2」と出力されますが、「重決定係数」はExcelだけの用語表現じゃないでしょうか。一般的ではないので論文に使わないようにしましょう。

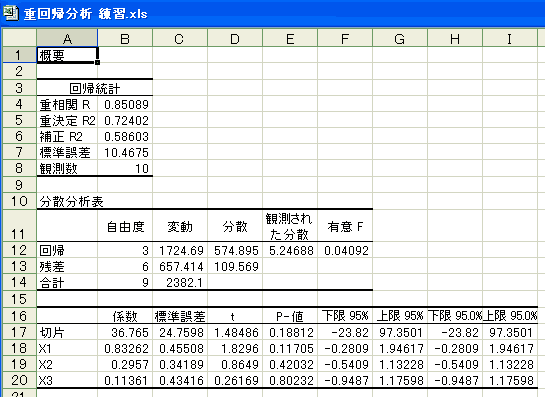
決定係数は、重回帰分析を行うとセットで出力される分散分析表からも、簡単に計算できます。分散分析表の一番下の行に「合計の変動」の欄がありますが、この値が示すものは、目的変数の平均値と観測された値との差の二乗の和（偏差平方和）です。目的変数のデータ全体のばらつきの大きさを示していて、総変動（St）という言い方もします。

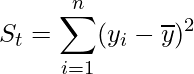
合計の一つ上の行の変動を誤差変動（Se）と言います。誤差変動は観測値と重回帰式による推定値の差（残差）の二乗の和です。回帰式で説明できなかった目的変数の変動（ばらつき）の大きさを示しています。

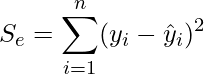
この総変動（St）と誤差変動（Se）を次の式にあてはめると決定係数（R²）が求められます。

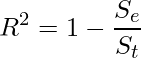
決定係数の意味するところは、目的変数の総変動のうち、重回帰式で説明できる変動の割合です。

決定係数（R²）は重相関係数（R）の二乗なので、逆に、決定係数を計算しておいて、そのルート（二乗根）を求めると重相関係数ということになります。

単相関係数と違って、重相関係数は二乗根で求めた値なので、マイナスになることはありません。そのため、説明変数が1個の回帰分析の場合、回帰係数の符号がマイナスの時は重相関係数に-1を掛けて単相関係数を求めます。