2019年11月統計検定2級の問題の解説(その2)
2019/11/30
カテゴリ:統計検定
タグ:2019年11月
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
- 問7:標準誤差に関する問題
- 問8:条件付き確率に関する問題
- 問9:確率と期待値に関する問題
- 問10:分布関数と確率密度関数に関する問題
- 問11:歪度に関する問題
- 問12:不偏推定量と一致推定量に関する問題
問7 [11]
標本平均の標準誤差SEは、不偏分散を![]() 、サンプルサイズをnとすると次の式から求められます。
、サンプルサイズをnとすると次の式から求められます。
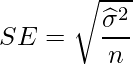
したがって、
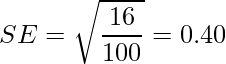
と計算できます。
問8 [12]
対策講座を受講する確率は20%であり、対策講座を受講した場合の合格率は70%であることから、無作為に選んだ1人が対策講座を受講した合格者である確率は次のように計算できます。
問8 [13]
全体の合格確率を求めます。合格確率を求めるには、①「対策講座を受講した受験者の合格確率」と②「対策講座を受講していない受験者の合格確率」を求める必要があります。①「対策講座を受講した受講者の合格確率」は[12]で求めたとおり0.14です。一方の②「対策講座を受講していない受験者の合格確率」は次のように計算できます。
これらをあわせた確率0.14+0.24が全体の合格確率です。この「全体の合格確率」に占める「対策講座の受講生の合格確率」が求める確率です。したがって、
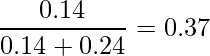
と計算できます。
問9 [14]
「全事象が起こる確率は1である」であることから、
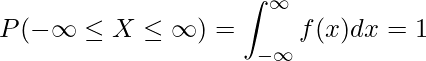
問題文より、次のような式を立てることができます。
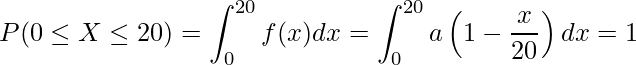
この式を整理すると、
![Rendered by QuickLaTeX.com \displaystyle \left[ax - \frac{ax^2}{40} \right]_{0}^{20} = 20a - 10a = 10a = 1](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-c3d780d35160c3b0267f9c3b082e8e40_l3.png)
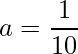
となります。
問9 [15]
確率密度関数f(x)の期待値は次の式から求められます。
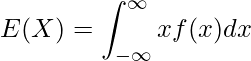
したがって、1ヶ月の水道使用量の期待値は次のように計算できます。
![Rendered by QuickLaTeX.com \displaystyle E(X) &=& \int_{0}^{20} \frac{x}{10}\left(1-\frac{x}{20}\right)dx \\ &=& \int_{0}^{20} \left(\frac{x}{10}-\frac{x^2}{200}\right)dx \\ &=& \left[\frac{x^2}{20} - \frac{x^3}{600} \right]_{0}^{20} \\ &=& \frac{400}{20} - \frac{8000}{400} \\ &=& \frac{20}{3}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-3cc0c4ee903a0874ae16b70989214c11_l3.png)
問9 [16]
まず、水道使用料金が1000円である![]() となる確率を求めます。
となる確率を求めます。
![Rendered by QuickLaTeX.com \displaystyle P(0 \leq x < 10) &=& \int_{0}^{10} \frac{1}{10}\left(1-\frac{x}{20}\right)dx \\ &=& \int_{0}^{10} \left(\frac{1}{10}-\frac{x}{200}\right)dx \\ &=& \left[\frac{x}{10} - \frac{x^2}{400} \right]_{0}^{10} \\ &=& 1 - \frac{100}{400} \\ &=& \frac{3}{4}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-7a22fbfea120a604d3f1406ec09dbea4_l3.png)
同様にして、水道使用料金が1120円である![]() となる確率を求めると、
となる確率を求めると、
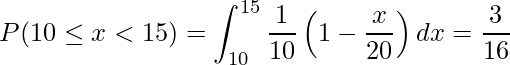
となり、水道使用料金が1280円である![]() となる確率を求めると、
となる確率を求めると、
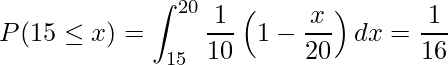
となります。これらの結果から1ヶ月の水道使用料金の期待値を求めると次のようになります。
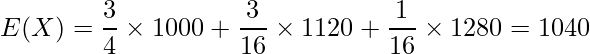
※このようにガリガリ計算をすると答えを得ることができますが、この問題は実のところここまで計算する必要はありません。水道使用料金は3パターン(1000円、1120円、1280円)しかないので、期待値は1000円~1280円の間の値であることが分かります。また、水道使用料金が1000円となる確率が3/4と算出できた時点で、期待値は1000円に近い値であると推測できます。したがってこの時点で期待値は②であるということが分かります。
問10 [17]
Zは正値確率変数であり、![]() のときにはZを、
のときにはZを、![]() のときには0であることから、
のときには0であることから、![]() の範囲のみを考えればよいことが分かります。すなわち、
の範囲のみを考えればよいことが分かります。すなわち、
となります。![]() なので、次の式が成り立ちます。
なので、次の式が成り立ちます。
問10 [18]
[17]より、
となることから、下側95%点は5となります。
問10 [19]
確率変数が連続型である場合、累積分布関数は確率密度関数を積分することで求められます。逆に、確率密度関数は累積分布関数を微分することで求められます。確率密度関数f(x)の期待値を求めるには、次の式を使います。
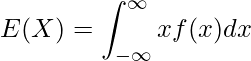
[17]で求めた![]() の両辺をxで微分すると
の両辺をxで微分すると![]() となります。したがって、確率変数Xの期待値は次の式から求められます。
となります。したがって、確率変数Xの期待値は次の式から求められます。
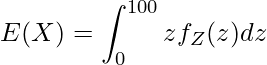
問11 [20]
I:× 歪度は分布の平均値とは関係がありません。正規分布からどのくらい歪んでいるかを表すための指標です。
II:× 歪度は、「右裾が長い」もしくは「右に歪んだ」もしくは「左に偏った」分布のときには正の値を、「左裾が長い」もしくは「左に歪んだ」もしくは「右に偏った」分布のときには負の値をとります。
III:× 歪度が0となるのは、左右対称の分布(例えば正規分布)の場合です。
問12 [21]
I:○
![]() の期待値は母平均に等しくなるため、不偏推定量であるといえます。
の期待値は母平均に等しくなるため、不偏推定量であるといえます。
II:×
一致推定量は、nが大きくなるにつれて真の母平均に近づく性質のことです。![]() の式では、nを大きくしたところで真の母平均には近づきません。
の式では、nを大きくしたところで真の母平均には近づきません。
III:○
![]() の期待値は母平均に等しくなるため、不偏推定量であるといえます。
の期待値は母平均に等しくなるため、不偏推定量であるといえます。
IV:○
![]() の式の場合、nが大きくなるにつれ真の母平均に近づきます。
の式の場合、nが大きくなるにつれ真の母平均に近づきます。








