母比率の区間推定における必要なサンプルサイズの計算フォーム
2017/12/19
カテゴリ:Tips
無限母集団から抽出したサンプルに含まれる、ある条件を満たす対象の比率(サンプル比率)が 母集団のそれと近い値であって欲しい場合、サンプル比率がある程度の誤差範囲内で 収まるために必要なサンプルサイズを、誤差、信頼度、母比率を指定することで求めることができます。
入力には半角数字を用いて、それぞれの範囲内の百分率で指定してください。
誤差(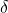 :デルタ)
:デルタ)
サンプル比率が母比率に対して上下何%の範囲内に収まって欲しいかを表します。
信頼度(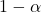 )
)
例えば、誤差を5%、信頼度を90%としたとき、これは100回中90回は サンプル比率と母比率との差が±5%の範囲内に収まることを意味します。
母比率(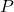 )
)
母集団に含まれる、ある条件を満たす対象の比率です。母比率の予測が困難な場合は50%とすると最も安全なサンプルサイズを求めることができます。
サンプルサイズ
母比率の区間推定は以下の式で行われます。
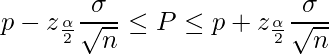
このとき、![]() は母比率、
は母比率、![]() はサンプル比率、
はサンプル比率、![]() はサンプルサイズ、
はサンプルサイズ、![]() は標準正規分布の上側100x%点、
は標準正規分布の上側100x%点、![]() (シグマ)は母比率の標準偏差です。
(シグマ)は母比率の標準偏差です。
このとき区間幅は、
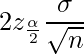
であり、これが一定値![]() 以下となるようにサンプルサイズを設計します。
以下となるようにサンプルサイズを設計します。
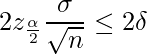
すなわち、
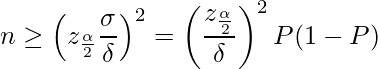
を満たす最小の![]() が最低限必要なサンプルサイズとなります。
ここで、
が最低限必要なサンプルサイズとなります。
ここで、![]() 、
、![]() 、
、![]() は小数値を用いています。
は小数値を用いています。
誤差を変化させたときのサンプルサイズの変化

信頼度と母比率の値を固定して誤差の値を変化させてみると、 上のグラフのように誤差を小さくするほど必要なサンプルサイズが増えることが見て取れます。
信頼度を変化させたときのサンプルサイズの変化

誤差と母比率の値を固定して信頼度の値を変化させてみると、 上のグラフのように信頼度を高くするほど必要なサンプルサイズが増えることが見て取れます。
母比率を変化させたときのサンプルサイズの変化

誤差と信頼度の値を固定して母比率の値を変化させてみると、 上のグラフのように母比率50%のところでサンプルサイズは最大値を取り、左右対称な曲線を描くことが見て取れます。
これは、母比率がわからないときは母比率を50%とするのが最も安全であるということを裏付けています。
ダウンロード
この統計TipのExcelファイルのダウンロードはこちらから → tips_13.xlsx
参考文献
関連記事
- Tips|母平均の区間推定における必要なサンプルサイズの計算フォーム
- Tips|2標本の母平均の差の区間推定における必要なサンプルサイズの計算フォーム
- コラム「統計備忘録」|幾つデータが必要か?―平均値の差の検定
- コラム「統計備忘録」|幾つデータが必要か?―比率の差の検定
- コラム「統計備忘録」|幾つデータが必要か?―相関係数の有意性検定
- コラム「統計備忘録」|幾つデータが必要か?―測定の信頼性による補正
- コラム「統計備忘録」|2群の比率の差の検定
- コラム「統計備忘録」|割合と比率
- コラム「統計備忘録」|割合、率、比
- コラム「統計備忘録」|比率が0%のときの信頼区間(3の法則)









