令和元年 公認会計士試験論文式試験(統計学)第8問 問題1
2021/06/21
カテゴリ:公認会計士(統計学)
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
問1
【ア】母集団から「完全に」・「ランダムに」標本を抽出することを「単純無作為抽出」といいます。
【イ】これは中心極限定理に関する問題です。中心極限定理は、平均![]() 、分散
、分散![]() に従う母集団からサンプルサイズnの標本を抽出する場合、その平均値の分布はnが大きくなるにつれて正規分布
に従う母集団からサンプルサイズnの標本を抽出する場合、その平均値の分布はnが大きくなるにつれて正規分布![]() に近づくというものです。したがって、標本平均
に近づくというものです。したがって、標本平均![]() の期待値は
の期待値は![]() となります。
となります。
【ウ】【エ】こちらも中心極限定理から、標本平均![]() の分散は
の分散は![]() となります。ただし、有限母集団から標本を抽出する場合、標本を抽出するたびに母集団のデータがどんどん減ってしまうために推定値に偏りが出てしまう可能性があります。そこで
となります。ただし、有限母集団から標本を抽出する場合、標本を抽出するたびに母集団のデータがどんどん減ってしまうために推定値に偏りが出てしまう可能性があります。そこで![]() をかけて「有限母集団修正」を行います。
をかけて「有限母集団修正」を行います。
【オ】母集団をあらかじめいくつかの層(グループ)に分けておき、各層の中から必要な数の調査対象を無作為に抽出する方法を「層化抽出法」もしくは「層別抽出法」といいます。
【カ】iグループのj番目のサンプルの値を![]() とおきます。問題文より
とおきます。問題文より
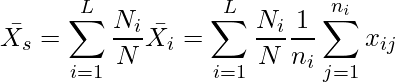
ここで、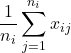 の期待値は
の期待値は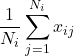 となるので、
となるので、
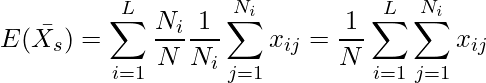
となります。この式より、![]() は次のようになります。
は次のようになります。
【キ】【ク】![]() は互いに独立なので、
は互いに独立なので、
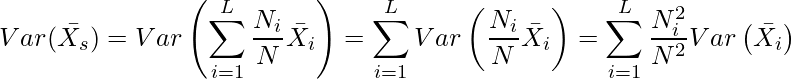
問題文の上の方で![]() の式が算出されているのでこの式を使うと、
の式が算出されているのでこの式を使うと、
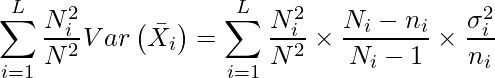
となります。
問2
「1~9人」の場合
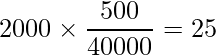
「10~99人」の場合
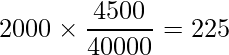
「100~999人」の場合
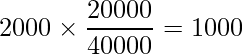
「1000人以上」の場合
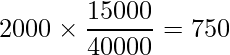
問1より![]() の分散
の分散![]() は
は
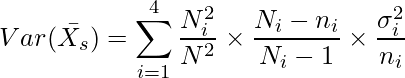
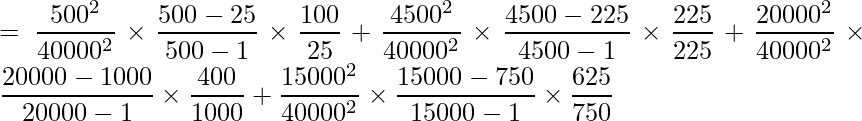
となります。この値の平方根を取ることで標準誤差となります。
問3
問1より
であることから、![]() は不偏推定値です。したがって、求める値は、
は不偏推定値です。したがって、求める値は、
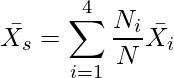
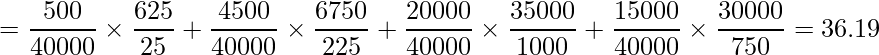
となります。








