2014年6月統計検定2級の一部問題の解説

2017/05/30

タグ：2014年6月

※統計検定2級解説記事一覧はこちら※

問8：連続型確率変数の確率密度関数から期待値と分散を求める問題
問9：偏差値に関する問題
問11：2標本の検定関する問題
問12：条件付き確率の問題
問13：さいころの出る目についての検定問題
問14：統計用語の問題
問15：t検定の問題
問16：調査方法に関する問題
問17：クロス集計表の検定に関する問題
問18：回帰分析に関する問題

問8（回答番号11,12）

■回答番号11

$\displaystyle E[X]=\int_{0}^{2} xf(x) = \int_{0}^{2} 0.5x^2 = \left[\frac{1}{6}x^3\right]_{0}^{2}=\frac{8}{6}=\frac{4}{3}$

■回答番号11

$\displaystyle E[X^2]=\int_{0}^{2} x^2f(x) = \int_{0}^{2} 0.5x^3 = \left[\frac{1}{8}x^4\right]_{0}^{2}=\frac{16}{8}=2$

$\displaystyle V[X]=E[X^2]-E[X]^2=2-\left(\frac{4}{3}\right)^2=\frac{2}{9}$

問9（回答番号13,14）

■回答番号13

A君の偏差値

$\displaystyle \frac{75-60}{15} \times 10 + 50 = 60$

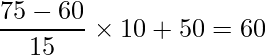
B君の偏差値

$\displaystyle \frac{70-60}{15} \times 10 + 50 = 56.7$

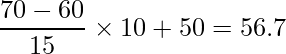
■回答番号14

A君の得点を標準化すると1なので、標準正規分布表より、A君の得点より低い人は全体の約84.1%である。B君の得点を標準化すると2/3≒0.67なので、標準正規分布表より、B君の得点より低い人は全体の約74.9%である。

よって、求める値は、500×（0.841-0.749）≒46人

問11（回答番号16,17）

■回答番号16

母分散未知で2つの分散が等しい場合はt検定を行う。t検定における合成した分散は以下の式で求められる。

$\displaystyle s^2=\frac{199s_{A}^2+199s_{B}^2}{398}=\frac{s_{A}^2+s_{B}^2}{2}$

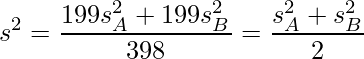
■回答番号17

母分散未知で2つの分散が等しい場合はt検定を行う。

問12（回答番号18,19）

■回答番号18

不良品が含まれている確率をP(X)、A社のボールペンが選ばれる確率をP(A)、B社のボールペンが選ばれる確率をP(B)とします。

求めたい確率はP(X|A)＋P(X|B)です。

したがって、P(X|A)＋P(X|B)=0.6×0.01＋0.4×0.05=0.026となります。

■回答番号19

求めたい確率はP(X|B)を全体の不良率｛P(X|A)＋P(X|B)｝で割ったものです。

P(X|B)=0.4×0.05=0.02なので、0.02/0.026=0.77となります。

問13（回答番号20,21,22）

■回答番号20

落ち着いて考えれば簡単なはず！

■回答番号21

3の目が4回出たことに基づいて検定を行います。つまり、4回出たことが偶然なのか、偶然ではなくさいころがおかしいからなのかを検定するわけです。

「3の目が4回出る」という事象の中には、「3の目が4回だけ出る」「3の目が5回だけ出る」「3の目が6回だけ出る」「3の目が7回だけ出る」という4つのパターンが含まれます。したがって、これら4パターンの確率全てを足した値を用いて検定を行う必要があります。

◯正しい。
×「4回だけ」の確率を扱うというのは誤り。
×これについて検定を行うのであって・・・
×「4回未満」の確率を扱うというのは誤り。
×「4回前後」の確率を扱うというのは誤り。

■回答番号22

3が4回出る確率を6倍すれば良いので、0.015629×6=0.094

問14（回答番号23）

■回答番号23

落ち着いて考えればきっと分かるはず！

問15（回答番号24,25,26,27）

■回答番号24

支店長の店（支店A）のアンパンが基準よりどうか、ということが問題になっている。
「105ｇで作ることになっている」のだから、（アンパンの母平均が）「105g」かどうかを検討すればよい。
統計的な仮説検定では、「帰無仮説に具体的な値が設定できる」ことが必要なので帰無仮説は「●●である」系になる。

■回答番号25

1標本のt検定で検定統計量（t統計量）をどうやって作るかは、残念ながら覚えるしかない。

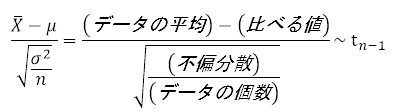
「●~▲」みたいなのは「●は▲分布に従う」の意味。あとは問題文中の数値を代入するだけだが、与えられた数値が分散なのか標準偏差なのかは注意すること。値を代入して計算すると「だいたい2.55」。

■回答番号26

母分散が分かっていないのでt検定になる（問題文にも書いてあるが）
参照するt分布の自由度はデータの数26よりも1少ない「25」であること
「アンパン105gより重いか」なので重かったらダメ、つまり片側検定
片側検定では、有意水準の値の半分のパーセント点を参照する
このタイプの片側検定では「検定統計量>「分布表から読み取った値」」なら有意

■回答番号27

1標本の母平均の信頼区間も残念ながら覚えるしかない。信頼係数αの信頼区間の式は↓のようになる。後は数値を代入するだけ。実はtの具体的な値は、前問で読み取った値ではなく、2.5%点である「t=2.060」を使う。あとは全部値を突っ込めば答えが出る。

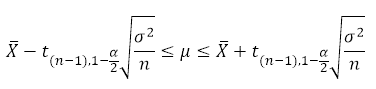
具体的に値を出すと「105.19～106.8」。信頼区間も105を含んでいないことに注目。

問16（回答番号28,29）

■回答番号28

取ってきたデータの男女比が～という問題なので、これを比較するには比率か度数で検定を行えばよい。具体的にはカイ二乗検定かZ検定になる。分散を検定しても意味がない。

■回答番号29

やや悪問。怪しい選択肢がいくつかあるが、「最も適切なもの」を選ぶ。方向性としては、「性別で満足度に違いがあるかどうか」→「男女で満足度の回答傾向は同じか（関連はあるか）」→「回答傾向は独立であると考えられるか」

×平均と中央値比べてどうするのか謎。実際何かできそうだが回りくどい。
×四分位範囲比べても無意味。
◯これが正解。
×分散を検定しても無意味。2と同じ理由で不適。
×そもそも男女比違う(6:4)から人数差比べる意味がない。

問17（回答番号30,31）

■回答番号30

クロス集計表で周辺度数から理論度数を計算するだけ。

	項目3	項目4	合計
項目1	A	B	A+D
項目2	C	D	C+D
合計	A+C	B+D	A+B+C+D

「独立である」とは、「どの列」「どの行」を切り取っても、「周辺度数の比と同じ」である状態。上の例では、項目3の列で縦に切ってみると、「A:C=(A+D):(C+D)」の比の関係になるし、項目2の行で横に切ってみると、「C:D=(A+C):(B+D)」になる、という感じ。そうなるような度数が独立性の検定での理論度数になる。

具体的にはセルごとに「（そのセルの行和）×（そのセルの列和）÷（総和）」で計算できる。したがって、200×240÷400=120

■回答番号31

悪問に見える。選択肢の文章が変。クロス表に関わるカイ二乗検定のポイントは↓の3つ。

カイ二乗統計量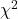（ $\chi^2$ 値）は、「セルごと計算して」、「全部足す」
自由度は、集計表の「（列の数-1）×（行の数-1）」になる。2×2集計表なら自由度は1
分布表の上側の（有意水準）％点から比較し、カイ二乗値がそれより大きければ有意

自由度1のカイ二乗分布の上側5％点は「3.84」。検定統計量の方が大きいので有意。以下は各選択肢のポイント。

×「有意水準」と比べるのは「P値」。「検定統計量」と比べるのは「分布表から読み取った値（棄却限界値という）」。混同しないよう注意。
×自由度がおかしい、しかも検定の解釈の方法がおかしい。
×自由度がおかしい、しかも検定の解釈の方法がおかしい。
×カイ二乗値の計算方法がおかしい。割ってはダメ。
◯これが正解。

問18（回答番号32,33）

落ち着いて考えれば難しくない問題です。ただし、この問題を解くために十分な時間を残しておくことが必要です（統計検定2級の試験時間は90分）。

■回答番号32

「降水量の予測値=59.7858+4.8617×平均気温」の式に入れてみて考えます。

■回答番号33

I：×決定係数には差があります。B君のほうが良いです。

II：◯対数をとる前は、平均気温が高くなるほど降水量の分散が大きくなる傾向が見られていました。対数をとることによって、そのような傾向が解消されて、平均気温ごとの降水量の分散が均一化されたことが読み取れます。

III：×二人とも単回帰分析を行っており、説明変数の数に差はありません。したがって、わざわざ自由度調整済み決定係数を使って比較する必要はありません。

ブログ