2016年6月統計検定2級の一部問題の解説(詳細版)
2016/06/21
カテゴリ:統計検定
タグ:2016年6月
※統計検定2級 解説記事一覧はこちら※
2016年6月19日に統計検定が実施されました。今回の2級で出題された問題の中で、難しいと思われる問題をいくつかピックアップし、より詳細に解説をします。
この記事では、次の4問の解説をしています。下のリストからクリック、またはタップした問題の解説部分へジャンプします。
問7(回答番号16,17,18)
大学入試の二次試験で出てくるような問題でした。
回答番号18については、一切のヒントがない状態で解く場合にはかなり難易度が高いのですが、ヒントが与えられているので、16・17の誘導に乗れば難しくありません。
■回答番号16
このゲームにおいて、何戦目であっても、一回のゲームでどちらかが勝つ確率は変化しません。 つまり、各ゲームは独立であるので、「AがBに勝ち、Cに負け、その後優勝する」確率はそれぞれの確率の積で表せることが分かります。
勝負の流れを図で表すと、下のようになります。3戦目以降については、「Aが負けて、最終的に優勝する」までの流れは条件付き確率![]() で表せることから、具体的に誰と対戦して勝ったかについては省略できることから、このように表しています。
で表せることから、具体的に誰と対戦して勝ったかについては省略できることから、このように表しています。

これより、答えは次のように計算できます。
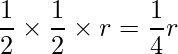
■回答番号17
問題文から、Aが勝つ確率は、「AがBに勝ち、Cに負け、その後優勝する」または、「Aが2連勝する」または、「Bに負け、その後優勝する」の3パターンがあることが分かります。この3つのパターンでAが優勝する確率をそれぞれ計算してみましょう。
- 「AがBに勝ち、Cに負け、その後優勝する」パターン
- 「Aが2連勝する」パターン
- 「Bに負け、その後優勝する」パターン
これは回答番号16で解いた通り、Aが優勝する確率は![]() です。
です。
このパターンを図で表すと、次のようになります。

このとき、Aが優勝する確率は![]() です。
です。
このパターンを図で表すと、次のようになります。

このとき、Aが優勝する確率は![]() です。
です。
これらの確率は排反であるので、このいずれかのパターンでAが優勝する確率は、この3つの確率の和となります。
つまり、Aが優勝する確率![]() は、以下のように計算できます。
は、以下のように計算できます。
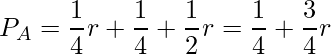
■回答番号18
回答番号17まで解けていれば、![]() は求められています。
は求められています。![]() と
と![]() も計算してみましょう。
も計算してみましょう。
【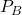 について】
について】
Bが優勝するパターンについても、Aと同様に3つのパターンに分けられます。
- 「BがAに勝ち、Cに負け、その後優勝する」パターン
- 「Bが2連勝する」パターン
- 「Aに負け、その後優勝する」パターン
このパターンを図で表すと、次のようになります。

このとき、Bが優勝する確率は![]() です。
です。
このパターンを図で表すと、次のようになります。

このとき、Bが優勝する確率は![]() です。
です。
このパターンを図で表すと、次のようになります。

このとき、Bが優勝する確率は![]() です。
です。
![]() と同様にこれらの確率は排反であるので、このいずれかのパターンでBが優勝する確率は、この3つの確率の和となります。
と同様にこれらの確率は排反であるので、このいずれかのパターンでBが優勝する確率は、この3つの確率の和となります。
つまり、Bが優勝する確率![]() は、以下のように計算できます。
は、以下のように計算できます。
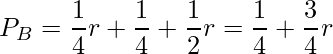
この結果、![]() であることがわかります。
であることがわかります。
【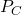 について】
について】
![]() についても、
についても、![]() や
や![]() と同様に3つのパターンで考えてみましょう。
と同様に3つのパターンで考えてみましょう。
これまでのパターンを一般化することができ、そうして解くと楽なのですが、今回は全てのパターンを列挙して解きます。
- 「AがBに勝ち、AとCが対戦してCが勝ち、BとCが対戦してCが負けるが、その後優勝する」パターン
- 「BがAに勝ち、BとCが対戦してCが勝ち、AとCが対戦してCが負けるが、その後優勝する」パターン
- 「AがBに勝ち、その後Cが2連勝する」パターン
- 「BがAに勝ち、その後Cが2連勝する」パターン
- 「AがBに勝ち、CがAに負けるがその後優勝する」パターン
- 「BがAに勝ち、CがBに負けるがその後優勝する」パターン
このパターンを図で表すと、次のようになります。

このとき、Cが優勝する確率は![]() です。
です。
このパターンを図で表すと、次のようになります。

このとき、Cが優勝する確率は![]() です。
です。
このパターンを図で表すと、次のようになります。

このとき、Cが優勝する確率は![]() です。
です。
このパターンを図で表すと、次のようになります。

このとき、Cが優勝する確率は![]() です。
です。
最初の対戦で負けるパターンです。![]() や
や![]() では考えたパターンですが、よく考えるとこれは成り立ちません。図で表してみましょう。
では考えたパターンですが、よく考えるとこれは成り立ちません。図で表してみましょう。


どちらの場合においてもCにとっては最初の対戦ですが、既にAとBが戦っているのでどちらかが1勝しており、Cが負けるとその時点でC以外の優勝が決定してしまいます。
つまり、Cは最初の勝負で負けることはできません。
以上のことから、Cが優勝する確率![]() は、以下のように計算できます。
は、以下のように計算できます。![]() 、
、![]() と同様にこれらの確率は排反であるので、それぞれの確率の和を取れば計算できます。
と同様にこれらの確率は排反であるので、それぞれの確率の和を取れば計算できます。
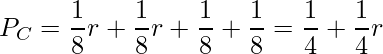
以上より、全ての確率が計算できました。rは0より大きいので、![]() となります。
となります。
問8(回答番号19,20)
統計検定2級において、積分を実際に計算する問題は2011年以降出題されていませんでした。
現役の大学生や高校生にとっては恐らく難しくないと思われますが、このタイプの問題は出ないと油断していた社会人の受験者の中には、意表を突かれた方もいらっしゃるのではないでしょうか。
■回答番号19
数理統計学的に厳密な定義ではありませんが、連続型確率変数Xについて、累積分布関数が![]() 、確率密度関数が
、確率密度関数が![]() で表される場合、中央値mは次のようにして定義できます。
で表される場合、中央値mは次のようにして定義できます。
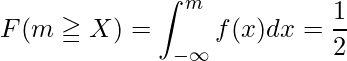
この問題では累積分布関数が与えられているので、次のように中央値を計算できます。
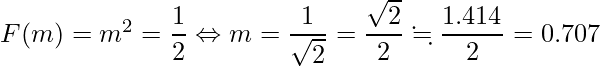
■回答番号20
連続型確率分布における分散Vは次の式によって計算できます。
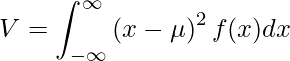
ここで、![]() は分布の平均値です。
は分布の平均値です。![]() は次の式によって計算できます。
は次の式によって計算できます。
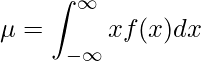
与えられた分布は、![]() 以外の範囲では
以外の範囲では![]() であるため、積分区間は0から1までを考えればよいことが分かります。
であるため、積分区間は0から1までを考えればよいことが分かります。
また、確率密度関数![]() は、次の計算により
は、次の計算により![]() であることがわかります。
であることがわかります。
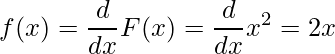
これを用いて、まず![]() を計算します。
を計算します。
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \mu&=\displaystyle\int_{-\infty}^{\infty} x f(x) dx \\ &=\displaystyle\int_{-\infty}^{0} x \cdot 0 dx + \displaystyle\int_{0}^{1} x f(x) dx \\ &\quad + \displaystyle\int_{1}^{\infty} x \cdot 0 dx \\ &=\displaystyle\int_{0}^{1} x \cdot 2x dx \\ &= \left[ \displaystyle \frac{2x^3}{3} \right]^1_0=\displaystyle \frac{2}{3} \end{split} \end{equation*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-0755e9932526553d2b02c0f6fe62f0d5_l3.png)
次に、![]() を用いてVを計算します。
を用いてVを計算します。
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} V&=\displaystyle\int_{-\infty}^{\infty} \left( x- \displaystyle \frac{2}{3} \right)^2 f(x) dx \\ &=\displaystyle\int_{-\infty}^{0} \left( x- \displaystyle \frac{2}{3} \right)^2 \cdot 0 dx + \displaystyle\int_{0}^{1} \left( x- \displaystyle \frac{2}{3} \right)^2 f(x) dx \\ &\quad + \displaystyle\int_{1}^{\infty} \left( x- \displaystyle \frac{2}{3} \right)^2 \cdot 0 dx \\ &=\displaystyle\int_{0}^{1} \left( x- \displaystyle \frac{2}{3} \right)^2 \cdot 2x dx \\ &=\displaystyle\int_{0}^{1} \left( 2x^3 - \displaystyle \frac{8}{3}x^2+ \displaystyle \frac{8}{9}x \right) dx \\ &= \left[ \displaystyle \frac{x^4}{2} - \displaystyle \frac{8x^3}{9} +\displaystyle \frac{4x^2}{9} \right]^1_0 \\ &=\displaystyle \frac{1}{2} - \displaystyle \frac{8}{9} + \displaystyle \frac{4}{9} \\ &=\displaystyle \frac{1}{18}=0.0555\cdots =0.056 \end{split} \end{equation*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-f79e7fe7e78d1eebe1742358d4f82906_l3.png)
よって、求める分散は0.056です。
なお、この問題は分散の別の計算式![]() を用いて計算することもでき、こちらの方が計算が簡単です。
を用いて計算することもでき、こちらの方が計算が簡単です。
この場合、次のようにVを計算できます。
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} V&=\displaystyle\int_{0}^{1} x^2 f(x) dx - \displaystyle\int_{0}^{1} x f(x) dx \\ &=\displaystyle\int_{0}^{1} 2x^3 dx - \mu^2 \\ &=\left[ \displaystyle \frac{x^4}{2} \right]^1_0 - \left( \displaystyle \frac{2}{3} \right)^2 \\ &=\displaystyle \frac{1}{2} - \displaystyle \frac{4}{9}=\displaystyle \frac{1}{18} \end{split} \end{equation*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-28ac36e736226d1f4e8263b7570eb0e8_l3.png)
問9(回答番号21,22)
推定量、という単語に驚くかもしれませんが、標本平均値の従う平均と分散についてと、変動係数について理解していれば解けます。
■回答番号21
母集団の平均が![]() 、分散が
、分散が![]() であるとき、大きさnの標本の平均値
であるとき、大きさnの標本の平均値![]() は次のように計算できます。
は次のように計算できます。
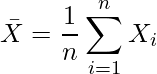
この![]() は、母平均
は、母平均![]() の推定量となっています。
の推定量となっています。
![]() の期待値(平均値)は
の期待値(平均値)は![]() で、分散は
で、分散は![]() です。
です。
変動係数は、![]() で計算することができるので、推定量の変動係数
で計算することができるので、推定量の変動係数![]() は次のようになります。
は次のようになります。
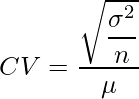
■回答番号22
回答番号21で求めた変動係数が0.05以下となればよいことから、次の不等式を考えます。
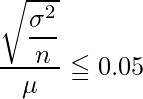
問題文から、母集団の変動係数が0.8以下であることが分かっているので、母集団における変動係数![]() が出てくるように変形します。
が出てくるように変形します。
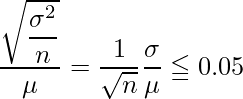
ここで、母集団における変動係数を![]() と置き換えると、次のように変形できます。
と置き換えると、次のように変形できます。
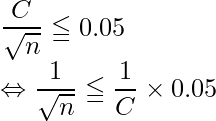
今回の場合、Cもnも負の値とはならないので、次のように変形できます
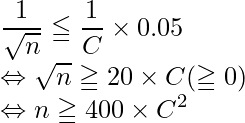
問題文より![]() であるので、
であるので、![]() のときに、問題の条件を満たす最小の
のときに、問題の条件を満たす最小の![]() が計算できます。
が計算できます。
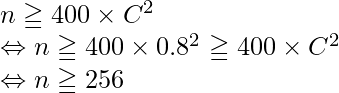
問12(回答番号29)
統計検定2級において、検出力を具体的に計算する問題が出題されるのは初めてなので、戸惑った方もいるのではないでしょうか。
この問題は、3つのステップに分けて解くと分かりやすいです。
- 棄却限界における
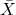 の値を求める。
の値を求める。 - 対立仮説の下で
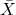 が従う分布を求める。
が従う分布を求める。 - 対立仮説の下で、
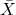 が1で求めた棄却限界を上回る確率を計算する。
が1で求めた棄却限界を上回る確率を計算する。
では、実際に解いていきましょう。
- 棄却限界における
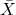 の値を求める。
の値を求める。 - 対立仮説の下で
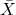 が従う分布を求める。
が従う分布を求める。 - 対立仮説の下で、
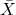 が1で求めた棄却限界を上回る確率を計算する。
が1で求めた棄却限界を上回る確率を計算する。
問題文から、棄却域は次のように設定されます。
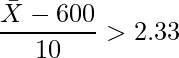
この式を変形し、具体的に![]() がどの値なら棄却されるかを計算します。
がどの値なら棄却されるかを計算します。
これは![]() が623.3を境界として、それより大きければ
が623.3を境界として、それより大きければ![]() が棄却されることを示しています。逆に、623.3以下なら棄却されません。
が棄却されることを示しています。逆に、623.3以下なら棄却されません。
対立仮説の下でラットの体重Xが従う分布は、平均630、標準偏差50の正規分布です。
正規分布の再生性から、![]() の従う分布は平均630,標準偏差
の従う分布は平均630,標準偏差![]() 10の正規分布であることが分かります。
10の正規分布であることが分かります。
1.で求めた棄却限界と、帰無仮説・対立仮説のもとで![]() が従う分布を図示すると、次のようになります。
が従う分布を図示すると、次のようになります。
青いほうが帰無仮説の下で従う分布で、オレンジ色の方は対立仮説の下で従う分布です。それぞれ、![]() と
と![]() です。
です。

![]() の従う分布が分かったので、これが棄却限界623.3を上回る確率を計算します。正規分布の上側累積確率が答えです。
の従う分布が分かったので、これが棄却限界623.3を上回る確率を計算します。正規分布の上側累積確率が答えです。
検出力に対応する部分を図示すると、次のようになります。図のオレンジ色の部分の面積が、検出力の値となります。

正規分布の累積分布関数を![]() とすると、この面積は次のように計算できます。
とすると、この面積は次のように計算できます。