Excelの機能だけでロジスティック回帰分析を実行する方法
2016/09/27
カテゴリ:エクセル統計
タグ:Excel
Excelの機能だけでロジスティック回帰分析を実行する方法を解説します。
Excelの関数や「分析ツール」では、回帰分析や分散分析を行う機能が搭載されていますが、ロジスティック回帰分析は搭載されていません。
しかし、ロジスティック回帰分析の原理についての知識があれば、ソルバーを用いて最尤法によるロジスティック回帰分析を行うことができます。
ただし、今回紹介する方法は、求められた解が100%正しい保証がなく、偏回帰係数の検定を行うことが出来ないことに注意してください。正しい解を求められるかについては、使用するデータや分析に使用するソルバーの性能に依存します。
この方法では、計算の途中でソルバーを使用します。ソルバーが有効になっていない場合は『ソルバーを有効にする手順』によってソルバーを使用できるよう設定してください。
Excel 2013を用いて解説していますが、ソルバーが使用可能であれば別のバージョンのExcelでも同様の方法で実行できます。
使用するデータ
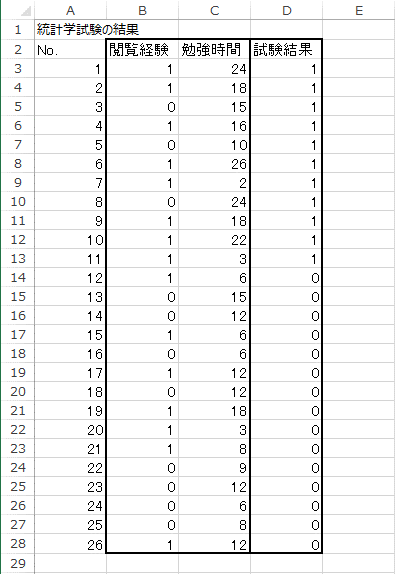
今回使用するデータは、統計学の時間(弊社の統計学についてのコンテンツ)の閲覧経験の有無と、統計学の試験勉強の時間を説明変数と、統計学の試験の合否を表す架空のデータです。
閲覧経験はダミー変数であり、0が「閲覧しなかった」ことを、1が「閲覧した」ことを表します。 また、「試験結果」は0が「不合格」を、1が「合格」をそれぞれ表します。
このデータから、統計学の試験の合否を予測する次のような二項ロジスティックモデルを作成します。
(試験に合格する確率)=![]() +
+ ![]() (閲覧経験の有無) +
(閲覧経験の有無) +![]() (勉強時間)
(勉強時間)
ロジスティック回帰分析の手順
前半:データの作成
前半では、分析するためのデータシートを作成します。
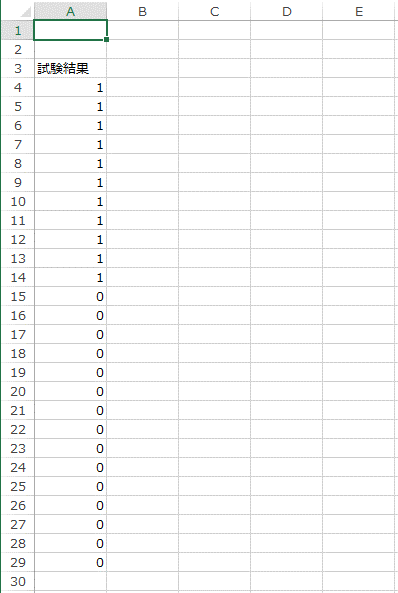
1. 新しいシートを作成し、元のデータシートの「D2:D28」をコピーし、新しいシートの「A3:A29」にペーストします。
2. 元のデータ「B2:C28」をコピーし、新しいシートの「C3:D29」にペーストします。
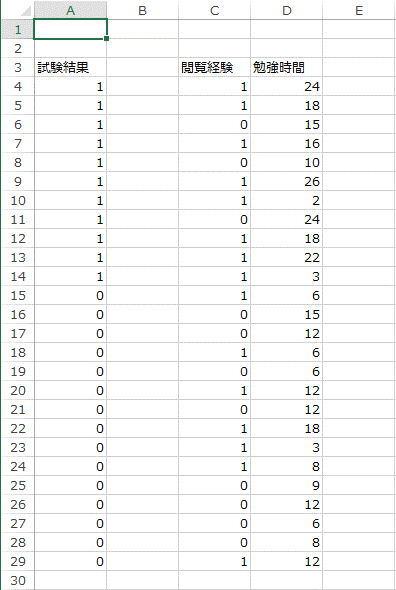
3. 次に、「B3」のセルに「定数項」と入力し、「B4:B29」のセル全てに「1」を入力します。
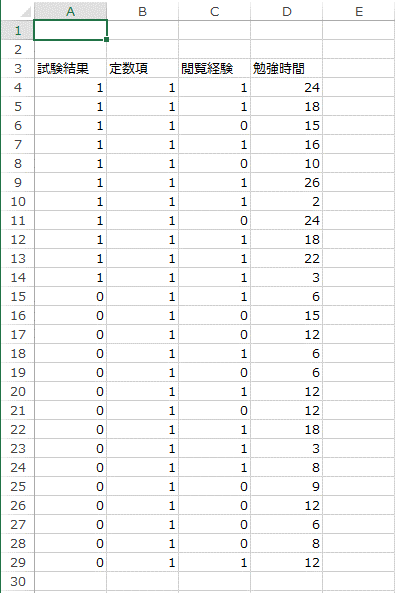
手順3まで完了すると、データは次のようになります。
A列は「試験結果」の変数列で、目的変数です。B列からD列は「定数項」、「閲覧経験」、「勉強時間」の変数列で、これらは説明変数です。
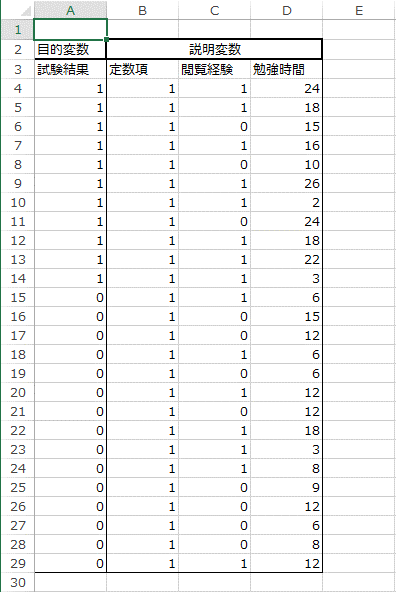
4. 「B1:D1」のセルに「0」を入力します。
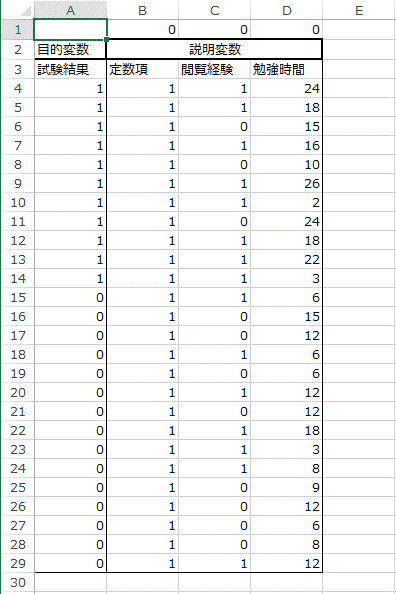
5. 「B1:D1」のセルは、「偏回帰係数の推定値」となります。 ソルバーによってこの値を変化させ、解を求めます。初期値として全ての偏回帰係数を「0」としています。
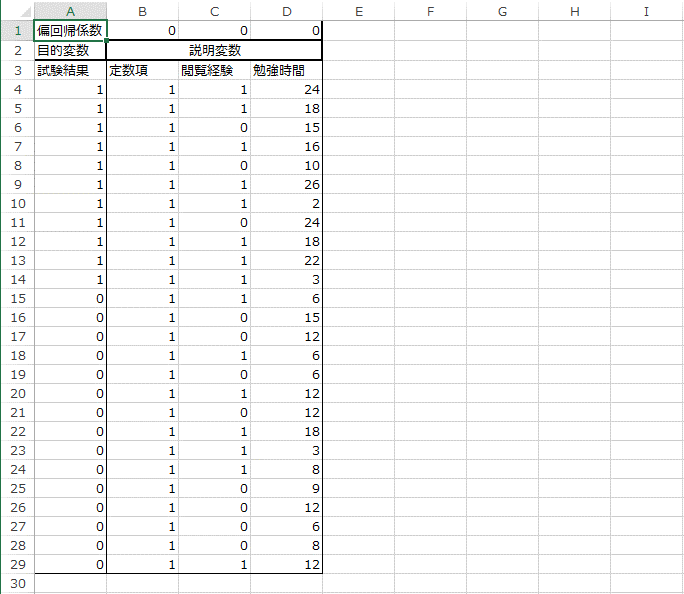
6. セル「E3」に「推定値」と入力します。
次に、セル「E4」に、下記の数式を入力し、Enterキーを押してください。
=1/(1+EXP(-SUMPRODUCT($B$1:$D$1,B4:D4)))
この式は、データごとにy=1となる確率の推定値![]() を計算しています。
を計算しています。
ここで使用したEXP関数は、指数関数を計算する関数です。
また、SUMPRODUCT関数は、引数の配列の積和を計算する関数です。
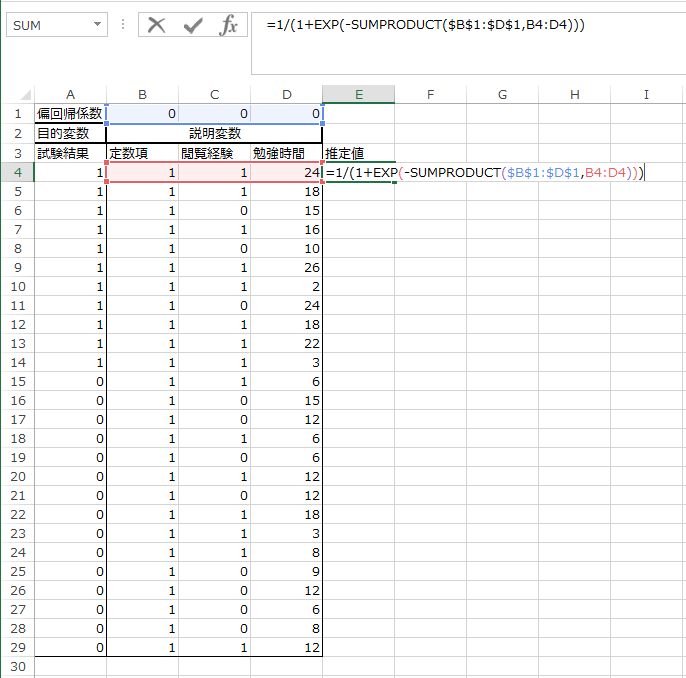
7. セル「E4」の右下の角にマウスポインタを当ててポインタの形が+に変わったら、そのままダブルクリックします。
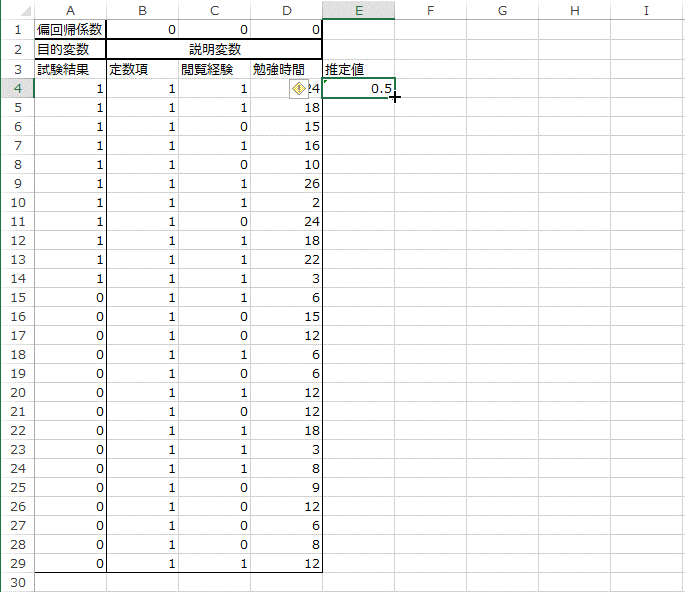
これで、セル「E5:E29」まで数式のオートフィルを行うことができます。
この操作が終わると、次のようになります。
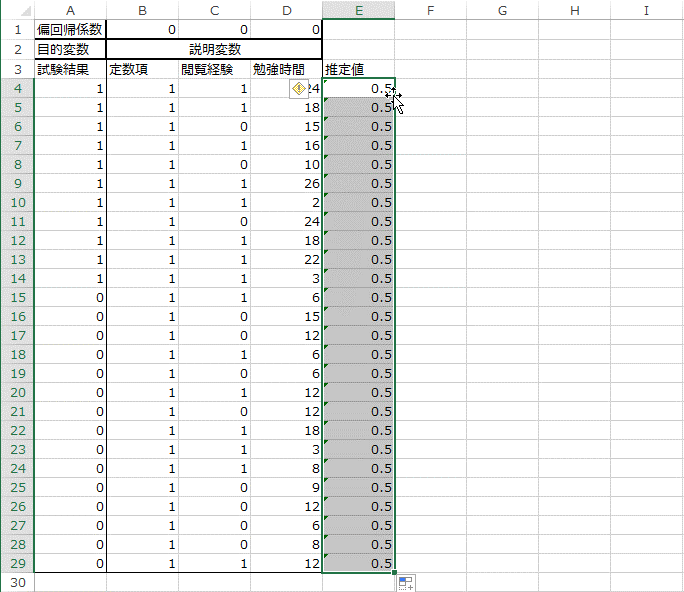
8. セル「F3」に「データごとの対数尤度」と入力します。
次に、セル「F4」に下記の数式を入力し、Enterキーを押します。
=A4*LN(E4)+(1-A4)*LN(1-E4)
これは、観測データ1つごとの対数尤度を計算しています。
ここで使用したLN関数は、引数の自然対数を計算する関数です。
9. セル「F4」の右下の角にマウスポインタを当ててポインタの形が+に変わったら、そのままダブルクリックします。
これで、「F5:F29」までオートフィルを行うことができます
この操作が終わると、次のようになります。
10. セル「G1」に「対数尤度」と入力します。
続いて、セル「H1」に下記の数式を入力し、エンターキーを押します。
=-2*SUM(F4:F29)
これは、モデル全体の対数尤度の総和をマイナス2倍したものを計算しています。
ここで使用したSUM関数は、配列の和を計算する関数です。
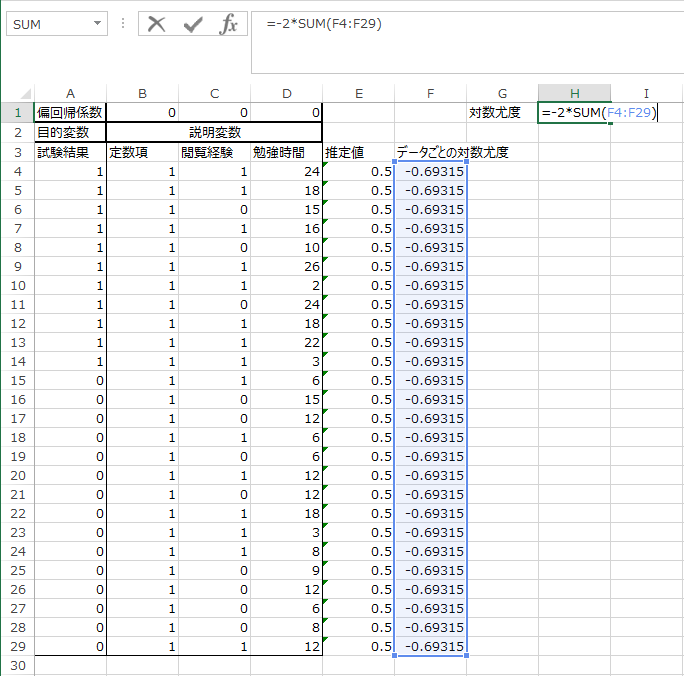
ここまで完了すると、シートは次のようになります。
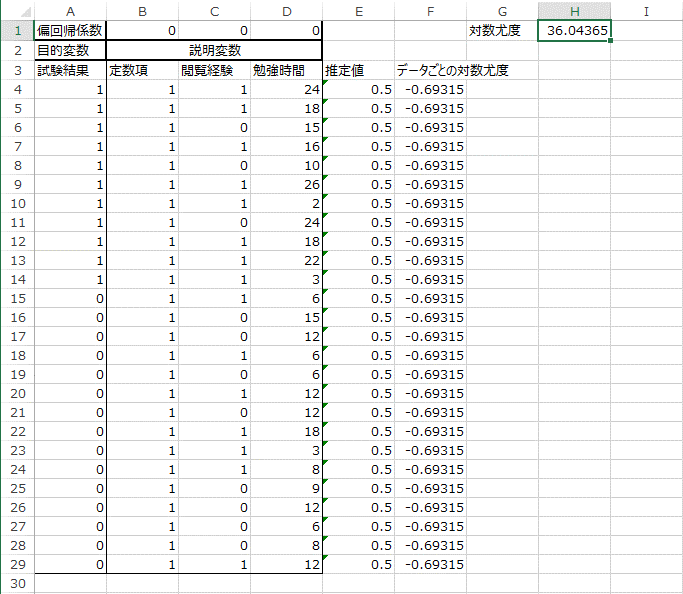
以上で前半部分であるデータの作成が完了しました。
後半:ソルバーを用いて計算する
後半は、ソルバーを用いて偏回帰係数の推定を行います。
11. セル「H1」を選択し、「データ」タブの「ソルバー」をクリックします。
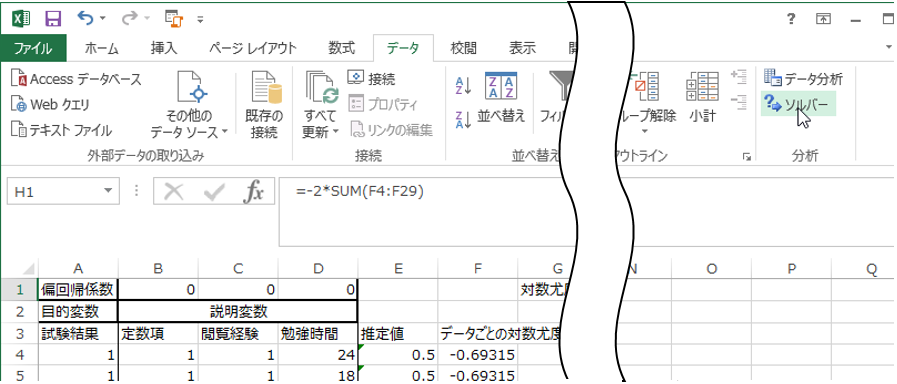
12. ソルバーのウィンドウが表示されます。「目的セルの設定」に「$H$1」と表示されていることを確かめます。
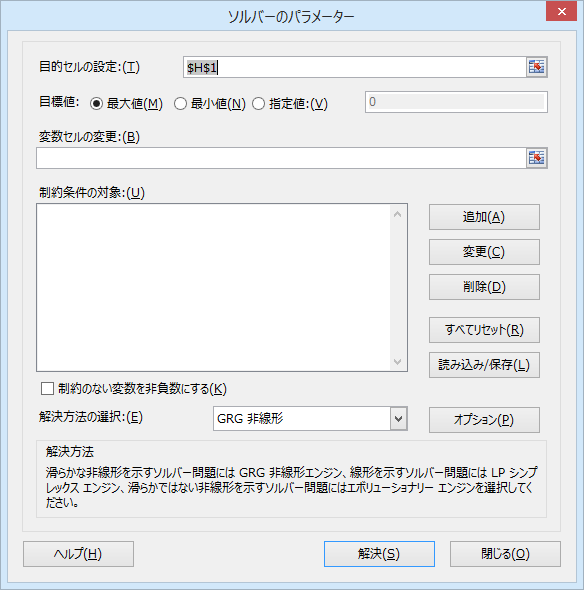
13. 「目標値」に「最小値」をクリックします。
14. 「変数セルの変更」に「$B$1:$D$1」と入力します。
15. もし、「制約のない変数を非負数にする」のチェックが入っている場合は、これを外します。
この操作まで終えると、ソルバーのウィンドウは次のようになります。
ソルバーの設定は以上で完了です。
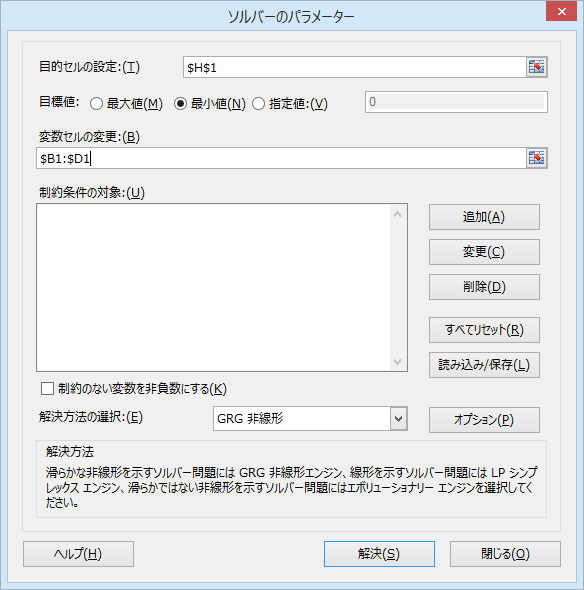
15. 「解決」をクリックします。
ソルバーは、「B1:D1」の3つの偏回帰係数の値を変化させながら、対数尤度のマイナス2倍が入力されたセル「H1」を最小化します。
この操作により、偏回帰係数を求めることが出来ます。
このように、対数尤度を変化させて解を求める方法を「最尤法」と言います。
計算が完了すると、次のような画面が表示されます。
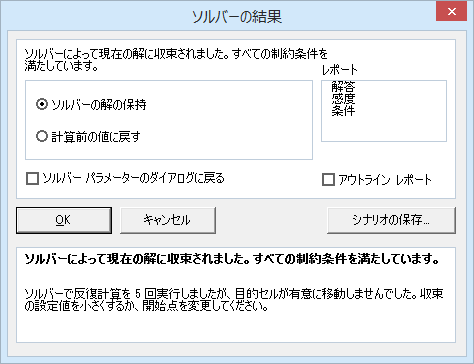
反復計算の結果、解が収束し計算が完了したことが分かります。
収束しなかった場合は、手順4をもう一度やり直し、ソルバーの設定を見直して再計算してください。
16. 偏回帰係数を確認します。偏回帰係数のセル「B1:D1」の数値が変化しています。
この結果から、このロジスティックモデルは
Ln(p/1-p)= -3.03+1.08×閲覧経験+0.166×勉強時間
と表されるようです。
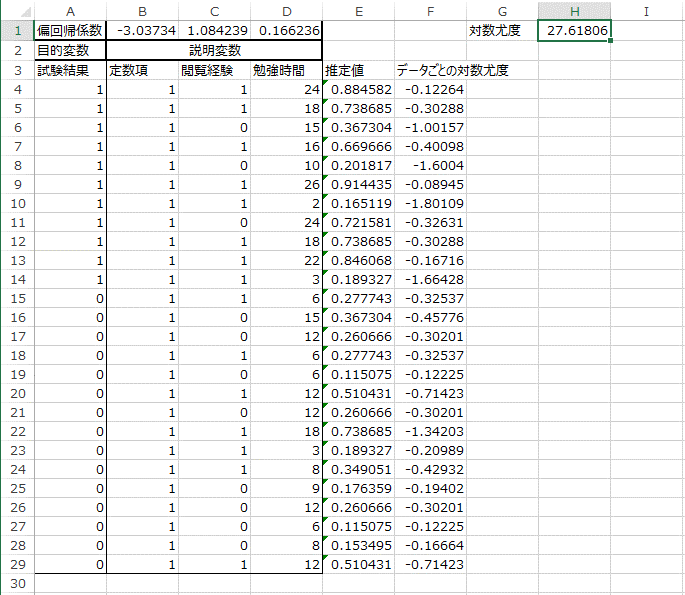
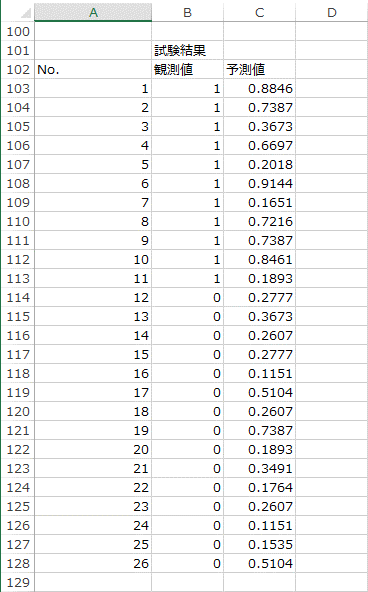
17. 推定値の部分も確認します。推定値は「y=1となる確率」であり、確かに「試験結果=1」のデータの方が「試験結果=0」のデータよりも確率が高くなっていることが分かります。
おまけ:エクセル統計の結果と比較する
このデータ例は、エクセル統計の分析例ファイルと同じものです。
エクセル統計の体験版をインストールすると、エクセル統計の分析例ファイルからこのデータのロジスティック回帰分析を実行できます。
Excelで解いた結果が正しいかどうかを、エクセル統計を用いて確認してみましょう。
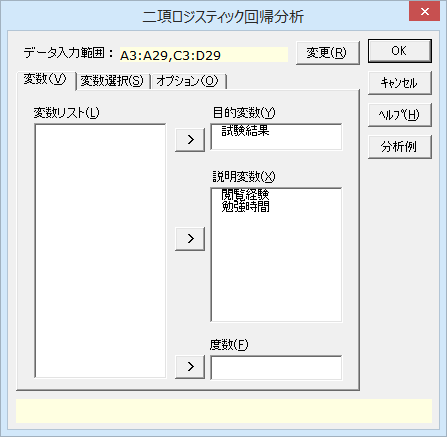
18. データを選択し、エクセル統計のタブから[多変量解析]→[二項ロジスティック回帰分析]を選択します。
19. [目的変数]に「試験結果」、[説明変数]に「閲覧経験」「勉強時間」を設定します。
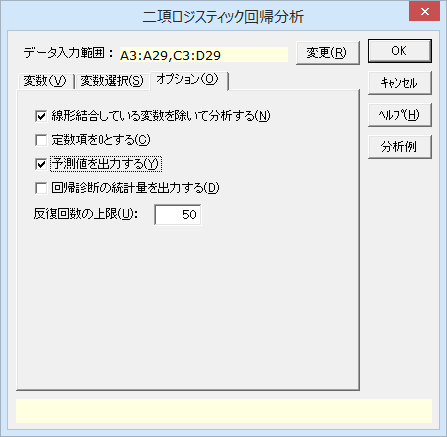
20. [オプション]タブをクリックし、「予測値を出力する」にチェックを入れ、「OK」をクリックします。
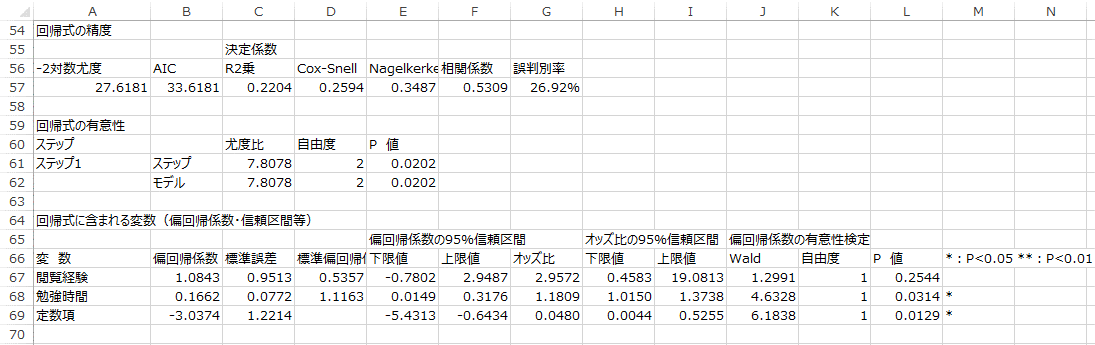
エクセル統計でロジスティック回帰分析を実行すると、次のような結果が出力されます。(クリックすると大きく表示されます。)
「-2対数尤度」と「偏回帰係数」がほぼ一致しており、Excelでもロジスティック回帰分析ができました。
予測値を参照すると、こちらもExcelで行った結果と一致しており、ソルバーでも正しい解が計算できていることが分かります。
このように、Excelでも簡単なロジスティック回帰分析を行うことが可能です。
しかしながら、偏回帰係数の標準誤差からP値を計算し、変数の有意性を検討するにはスコア関数と情報行列が必要となり、更に計算を行わなければいけません。
また、多重共線性の見られる変数を用いて分析を行った場合、解がうまく収束せず、誤った解が算出される可能性もあります。
統計解析ソフトを使用した方が、より簡単に、より多くの指標を計算することができます。
なお、エクセル統計ではこの方法で説明したソルバーを用いた計算は行っておらず、 統計解析手法における反復計算方法としてよく用いられる、ニュートン・ラフソン法により解を求めています。また、多重共線性がある変数をチェックする機能なども搭載しています。
ソルバーを有効にする手順
1. Excelの[ファイル]タブをクリックし、メニューから[オプション]をクリックします。
2. 「Excelのオプション」ウィンドウの[アドイン]をクリックします。
3. 「管理」のドロップダウンリストから[Excelアドイン]を選択し、「設定」をクリックします。
4. 「ソルバー アドイン」にチェックを入れ、「OK」をクリックします。以上で設定は完了です。